4.4: Enfoque bayesiano de las tasas evolutivas
- Page ID
- 53796
Finalmente, también podemos usar un enfoque bayesiano para ajustar modelos de movimiento brownianos a los datos y estimar la tasa de evolución. Este enfoque difiere del enfoque ML en que usaremos previos explícitos para valores de parámetros, y luego ejecutaremos un MCMC para estimar distribuciones posteriores de estimaciones de parámetros. Para ello, modificaremos el algoritmo básico para MCMC bayesiano (ver Capítulo 2) de la siguiente manera:
- Muestree un conjunto de valores de parámetros iniciales, σ 2 y $\ bar {z} (0) $ de sus distribuciones anteriores. Para este ejemplo, podemos establecer nuestra distribución anterior como uniforme entre 0 y 0.5 para σ 2 y uniforme de 0 a 10 para $\ bar {z} (0) $.
- Dados los valores actuales de los parámetros, seleccione nuevos valores de parámetros propuestos utilizando la densidad propuesta Q (p ′| p). Para ambos valores de parámetro, utilizaremos una densidad de propuesta uniforme con ancho w p, de manera que: (eq. 4.10)
\[ Q(p'|p) \sim U(p-\frac{w_p}{2}, p+\frac{w_p}{2}) \]
- Calcula tres proporciones:
- El odds ratio anterior, R p r i o r. Esta es la relación de la probabilidad de dibujar los valores de los parámetros p y p' del anterior. Ya que nuestros antecedentes son uniformes, esto siempre es 1.
- La relación de densidad propuesta, R p r o p o s a l. Esta es la relación de probabilidad de propuestas que van de p a p 'y a la inversa. Ya hemos declarado una densidad simétrica de propuesta, de manera que Q (p ′| p) = Q (p | p ′) y R p r o p o s a l = 1.
- El cociente de verosimilitud, R l i k e l i h o o d. Esta es la relación de probabilidades de los datos dados los dos valores de parámetros diferentes. Podemos calcular estas probabilidades a partir de la ecuación 4.5 anterior. (eq. 4.11)
\[ R_{likelihood} = \frac{L(p'|D)}{L(p|D)} = \frac{P(D|p')}{P(D|p)} \]
- Encuentre la relación de aceptación, R a c c e p t, que es producto de las probabilidades anteriores, la relación de densidad propuesta y la razón de verosimilitud. En este caso, tanto las probabilidades previas como las relaciones de densidad propuesta son 1, por lo que R a c c e p t = R l i k e l i h o d.
- Dibuja un número aleatorio x a partir de una distribución uniforme entre 0 y 1. Si x < R a c c e p t, acepte el valor propuesto de ambos parámetros; de lo contrario rechace, y conserve el valor actual de los dos parámetros.
- Repita los pasos 2-5 una gran cantidad de veces.
Usando los datos del tamaño corporal de los mamíferos, corrí un MCMC con 10,000 generaciones, descartando las primeras 1000 como burn-in. Muestreando cada 10 generaciones, obtengo estimaciones de parámetros de $\ hat {\ sigma} _ {bayes} ^2 = 0.10$ (intervalo de 95% creíble: 0.066 − 0.15) y $\ hat {\ bar {z}} (0) = 3.5$ (intervalo 95% creíble: 2.3 − 5.3; Figura 4.5).
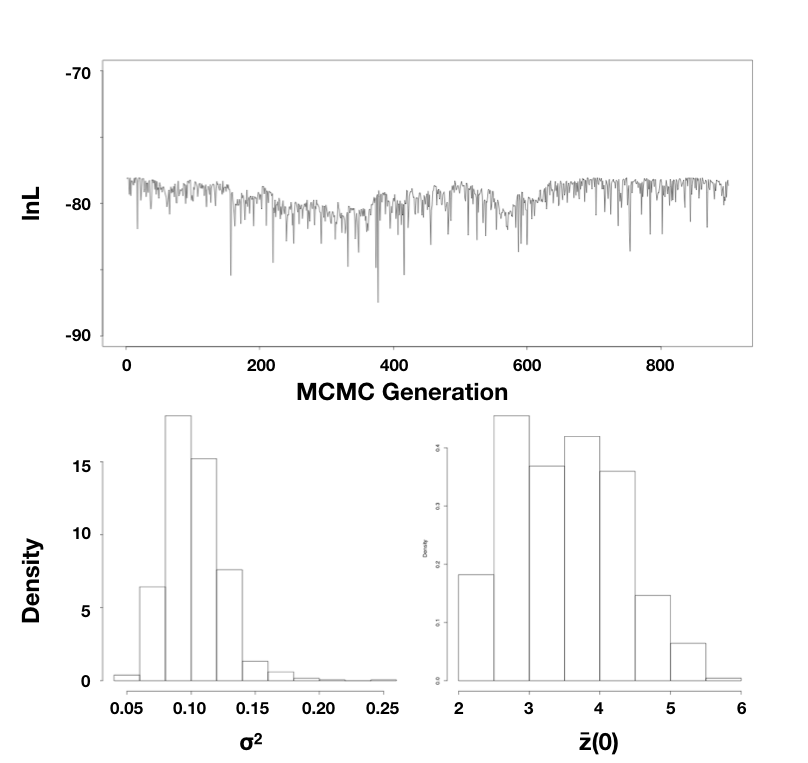
Tenga en cuenta que las estimaciones de los parámetros de los tres enfoques (REML, ML y Bayesiano) fueron similares. Incluso los intervalos de confianza/credibilidad variaron un poco pero fueron de aproximadamente el mismo tamaño en los tres casos. Todos los enfoques anteriores están matemáticamente relacionados y deben, en general, devolver resultados similares. Uno podría dar mayor valor a los intervalos bayesianos creíbles sobre los intervalos de confianza del hessian de la superficie de verosimilitud, por dos razones: primero, el hessiano conduce a una estimación del IC bajo ciertas condiciones que pueden o no ser ciertas para su análisis; y segundo, intervalos bayesianos creíbles reflejar la incertidumbre general mejor que los intervalos de confianza ML (ver capítulo 2).


