7.3: El modelo Mk

El modelo más básico para la evolución de caracteres discretos se llama el modelo Mk. Desarrollado por primera vez para datos de rasgos por Pagel (1994; aunque el nombre Mk proviene de Lewis 2001). El modelo Mk es un análogo directo del modelo Jukes-Cantor (JC) para la evolución de la secuencia. El modelo se aplica a un carácter discreto que tiene k estados desordenados. Tal carácter podría tener k = 2, k = 3, o incluso más estados. La evolución implica cambiar entre estos k estados (Figura 7.3).

Figura 7.3. Ejemplos de caracteres discretos con (A) k = 2, (B) k = 3, y (C) k = 4 estados. Imagen del autor, puede ser reutilizada bajo licencia CC-BY-4.0.

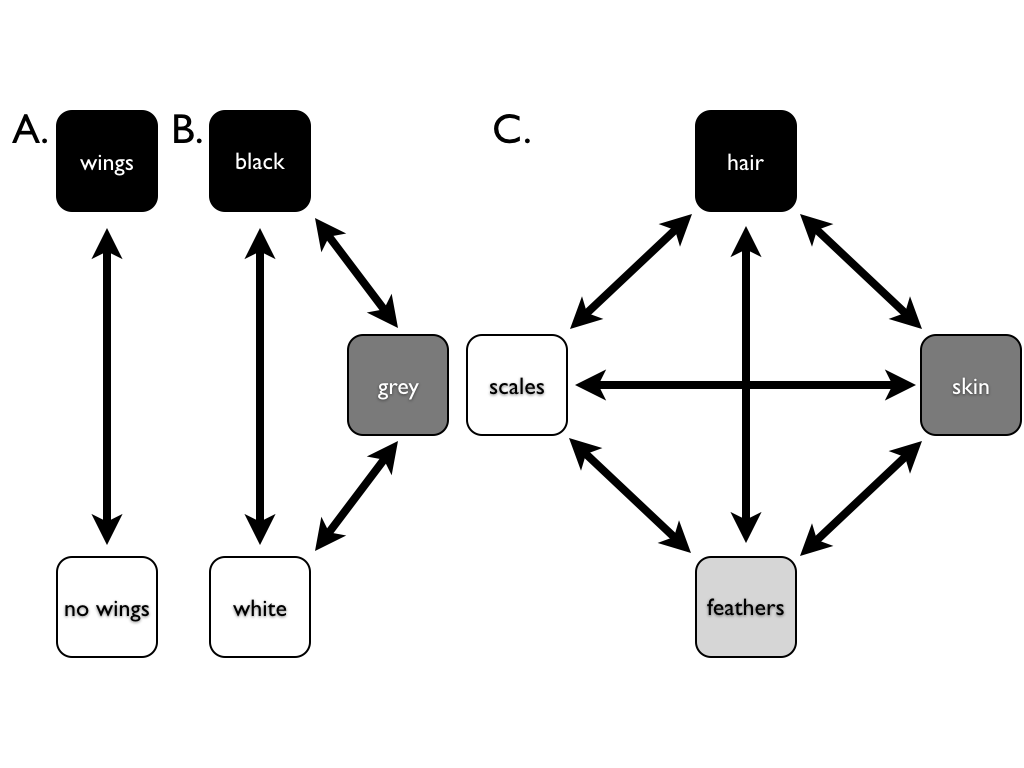
La versión básica del modelo Mk asume que las transiciones entre estos estados siguen un proceso de Markov. Esto significa que la probabilidad de cambiar de un estado a otro depende únicamente del estado actual, y no de lo que ha venido antes. Por ejemplo, no importa si un linaje acaba de evolucionar el rasgo de las “plumas”, o si han tenido plumas durante millones de años; la probabilidad de evolucionar un estado de carácter diferente es la misma en ambos casos. El modelo básico de Mk también asume que es igualmente probable que cada estado cambie a cualquier otro estado.

Para el modelo básico Mk, podemos denotar la tasa instantánea de cambio entre estados usando el parámetro q. En general, q _{i j} se llama la velocidad instantánea entre los estados de carácter i y j. Se define como el límite de la tasa medida en intervalos de tiempo muy cortos ¹.

Nuevamente, para el modelo básico de Mk, las tasas instantáneas entre todos los pares de caracteres son iguales; es decir, q _{i j} = q _{m n} para todos i ≠ j y m ≠ n.

Podemos resumir modelos generales de Markov para caracteres discretos usando una matriz de tasa de transición (Lewis 2001):

\[ \mathbf{Q} = \begin{bmatrix} -d_1 & q_{12} & \dots & q_{1k} \\ q_{21} & -d_2 & \dots & q_{2k} \\ \vdots & \vdots & \ddots & \vdots\\ q_{k1} & q{k2} & \dots & -d_k \\ \end{bmatrix} \label{7.1}\]

Tenga en cuenta que las tasas instantáneas solo se ingresan en las partes fuera de la diagonal de la matriz. A lo largo de la diagonal, estas matrices siempre tienen un conjunto de números negativos. Para cualquier matriz Q, la suma de todos los elementos en cada fila es cero, una condición necesaria para una matriz de tasa de transición. Debido a esto, cada número negativo tiene un valor, d _i, igual a la suma de todos los demás números de la fila. Por ejemplo,

\[ d_1 = \sum_{i=2}^{k} q_{1i} \label{7.2}\]

Para un modelo Mk de dos estados, k = 2 y las tasas son simétricas de manera que q ₁₂ = q ₂₁. En este caso, podemos escribir la matriz de tasa de transición como:

\[ \mathbf{Q} = \begin{bmatrix} -q & q \\ q & -q \\ \end{bmatrix} \label{7.3}\]

Asimismo, para k = 3, la matriz de velocidad de transición es:

\[ \mathbf{Q} = \begin{bmatrix} -2 q & q & q\\ q & -2 q & q\\ q & q & -2 q\\ \end{bmatrix} \label{7.4}\]

En general, la matriz de transición de estado k para un modelo básico de Mk es:

\[ \mathbf{Q} = \begin{bmatrix} 1-k & 1 & \dots & 1\\ 1 & 1-k & \dots & 1\\ \vdots & \vdots & \ddots & \vdots\\ 1 & 1 & \dots & 1\\ \end{bmatrix} \label{7.5}\]

Una vez que tenemos esta matriz de tasa de transición, podemos calcular la distribución de probabilidad de los estados de rasgo después de cualquier intervalo de tiempo t usando la ecuación (Lewis 2001):

\[\textbf{P}(t)=e^{\textbf{Q}t} \label{7.6}\]

Esta ecuación parece simple, pero calcular P (t) implica exponenciación matricial — elevando e a una potencia definida por una matriz. Este cálculo es sustancialmente diferente de elevar e a la potencia definida por cada elemento de una matriz ². El resultado es una matriz, P, de probabilidades de transición. Cada elemento de esta matriz (p _{i j}) da la probabilidad de que comenzando en el estado i termines en el estado j a lo largo de ese intervalo de tiempo t. Para el modelo Mk estándar, hay una solución general a esta ecuación:

\[ \begin{array}{l} p_{ii}(t) = \frac{1}{k} + \frac{k-1}{k} e^{-kqt} \\ p_{ij}(t) = \frac{1}{k} - \frac{1}{k} e^{-kqt} \\ \end{array} \label{7.7}\]

En particular, cuando k = 2,

\[ \begin{array}{l} p_{ii}(t) = \frac{1}{k} + \frac{k-1}{k} e^{-kqt} = \frac{1}{2} + \frac{2-1}{2}e^{-2qt}=\frac{1+e^{-2qt}}{2} \\ p_{ij}(t) = \frac{1}{k} - \frac{1}{k} e^{-kqt} = \frac{1}{2} - \frac{1}{2}e^{-2qt}=\frac{1-e^{-2qt}}{2} \\ \end{array} \label{7.8}\]

Si consideramos lo que sucede cuando el tiempo se hace muy grande en estas ecuaciones, vemos un patrón interesante. Cualquier término que tenga e ^{− t} en él se acerca cada vez más a cero a medida que t aumenta. Debido a esto, para todos los valores de k, cada p _{i j} (t) converge a un valor constante, 1/ k. Esta es la distribución estacionaria de los estados de carácter, π, definida como la frecuencia de equilibrio de los estados de carácter si el proceso se ejecuta muchas veces durante un período de tiempo suficientemente largo. En general, la distribución estacionaria de un modelo Mk es:

\[ \pi = \begin{bmatrix} 1/k & 1/k & \dots & 1/k\\ \end{bmatrix} \label{7.9}\]

En el caso de\(k = 2\),

\[ \pi = \begin{bmatrix} 1/2 & 1/2 \\ \end{bmatrix} \label{7.10}\]