11.2: Edad y diversidad del clado

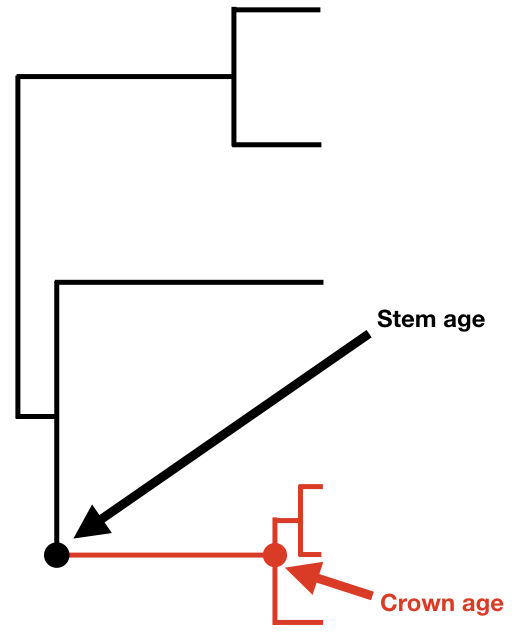
Si conocemos la edad de un clado y su diversidad actual, entonces podemos calcular la tasa neta de diversificación para ese clado. Antes de presentar ecuaciones, quiero hacer una distinción entre dos formas diferentes en las que se puede medir la edad de un clado: la edad del tallo y la edad de la corona. La edad de la corona de un clado es la edad del antepasado común de todas las especies del clado. Por el contrario, la edad del tallo de un clado mide el tiempo que ese clado descendió de un ancestro común con su clado hermano. La edad del tallo de un clado siempre es al menos tan vieja, y generalmente mayor, que la edad de la corona.

Figura 11.2. Edad de corona y tallo de un clado de interés (resaltado en rojo). Imagen del autor, puede ser reutilizada bajo licencia CC-BY-4.0.

Magallón y Sanderson (2001) dan una ecuación para la estimación de la tasa de diversificación neta dada la edad y diversidad del clado:

\[ \hat{r} = \frac{ln(n)}{t_{stem}} \label{11.1}\]

donde n es el número de especies en el clado en la actualidad y t s t _{e m} es la edad del grupo de tallo. En esta ecuación también vemos el parámetro de tasa de diversificación neta, r = λ − μ (ver Capítulo 10). Este es un buen recordatorio de que este parámetro predice mejor cómo las especies se acumulan a través del tiempo y refleja el equilibrio entre las tasas de especiación y extinción.

Alternativamente, se puede usar t _{c r o w n}, el grupo corona edad:

\[ \hat{r} = \frac{ln(n)-ln(2)}{t_{crown}} \label{11.2}\]

Las dos ecuaciones difieren porque en el grupo de la corona la edad uno está considerando la diversificación del clado comenzando con dos linajes en lugar de uno (Figura 11.2).

A pesar de que estas dos ecuaciones reflejan el equilibrio de nacimientos y muertes a través del tiempo, dan estimaciones de ML para r solo bajo un modelo de nacimiento puro donde no hay extinción. Si ha habido extinción en la historia del clado, entonces nuestras estimaciones utilizando las ecuaciones 11.1 y 11.2 serán sesgadas. El sesgo viene del hecho de que solo vemos clados que sobreviven hasta nuestros días, y se pierden cualquier clado de la misma edad que se extinguió antes de que pudieran ser observados. Al observar solo a los “ganadores” de la lotería de diversificación, sobreestimamos la tasa neta de diversificación. Si conocemos la cantidad relativa de extinción, entonces podemos corregir este sesgo.

Bajo un escenario con extinción, se puede definir = μ/λ y utilizar los siguientes estimadores de método de momentos de Rohatgi (1976, siguiendo la notación de Magallon y Sanderson (2001)):

\[ \hat{r} = \frac{log⁡[n(1-\epsilon)+\epsilon]}{t_{stem}} \label{11.3}\]

para la edad del tallo, y

\[ \hat{r} = \frac{ln[\frac{n(1-\epsilon^2 )}{2}+2 \epsilon+\frac{(1-\epsilon) \sqrt{n(n \epsilon^2-8\epsilon+2 n \epsilon+n)}}{2}]-ln(2)}{t_{crown}} \label{11.4}\]

para la edad de la corona. (Obsérvese que las eq. 11.3 y 11.4 reducen a 11.1 y 11.2, respectivamente, cuando = 0). Por supuesto, normalmente tenemos poca idea de lo que debería ser. La práctica común en la literatura es probar algunos valores diferentes para y ver cómo cambian los resultados (por ejemplo, Magallon y Sanderson 2001).

Magallón y Sanderson (2001), siguiendo a Strathmann y Slatkin (1983), también describen cómo usar las ecuaciones 10.13 y 10.15 para calcular los intervalos de confianza para el número de especies en un momento dado.

Como ejemplo trabajado, consideremos los datos del cuadro 11.1, que dan las edades y diversidades de copas de varios linajes vegetales en el Páramo (de Madriñán et al. 2013). Para cada linaje, he calculado la estimación de nacimientos puros de la tasa de especiación (a partir de la ecuación 11.2, ya que se trata de edades de la corona), y las tasas de diversificación neta bajo tres escenarios para extinción (= 0.1, = 0.5 y = 0.9).

Linaje	n	Edad	$\ hat {r} _ {pb} $	$\ hat {r} _ {\ épsilon = 0.1} $	$\ hat {r} _ {\ épsilon = 0.5} $	$\ hat {r} _ {\ épsilon = 0.9} $
1	17	0.42	5.10	5.08	4.53	2.15
2	14	10.96	0.18	0.18	0.16	0.07
3	32	3.80	0.73	0.73	0.66	0.36
4	65	2.50	1.39	1.39	1.28	0.78
5	55	3.05	1.09	1.08	1.00	0.59
6	120	4.04	1.01	1.01	0.94	0.62
7	36	4.28	0.68	0.67	0.61	0.34
8	32	7.60	0.36	0.36	0.33	0.18
9	66	1.47	2.38	2.37	2.19	1.34
10	27	8.96	0.29	0.29	0.26	0.14
11	5	3.01	0.30	0.30	0.26	0.09
12	46	0.80	3.92	3.91	3.58	2.07
13	53	14.58	0.22	0.22	0.21	0.12

La tabla anterior muestra estimaciones de las tasas de diversificación neta para linajes de Páramo (datos de Madriñán et al. 2013) utilizando las ecuaciones 11.2 y 11.4. Los linajes son los siguientes: 1: Aragoa, 2: Arcytophyllum, 3: Berberis, 4: Calceolaria, 5: Draba, 6: Espeletiinae, 7: Festuca, 8: Jamesonia + Eriosorus, 9: Lupino, 10: Lisipomia, 11: Oreobolus, 12: Puya, 13: Valeriana.

Inspeccionando las últimas cuatro columnas de esta tabla, podemos hacer algunas observaciones generales. Primero, estos linajes vegetales realmente tienen tasas de diversificación notablemente altas (Madriñán et al. 2013). Segundo, la tasa neta de diversificación que estimamos depende de lo que supongamos sobre las tasas de extinción relativas (). Se puede ver en la tabla que el efecto de la extinción es relativamente leve hasta que se supone que las tasas de extinción son bastante altas (= 0.9). Finalmente, asumir diferentes niveles de extinción afecta las tasas de diversificación pero no su ordenamiento relativo. En todos los casos, las tasas netas de diversificación para Aragoa, que formó 17 especies en menos de medio millón de años, son superiores a las del resto de los clados. Sin embargo, esta relación se mantiene solo cuando asumimos que las tasas de extinción relativas son constantes a través de los clados. Por ejemplo, la tasa neta de diversificación que calculamos para Calceolaria con = 0 es mayor que la tasa calculada para Aragoa con = 0.9. En otras palabras, no podemos ignorar completamente el papel de la extinción en la alteración de nuestra visión de los patrones de diversidad actuales.

También podemos estimar las tasas de nacimiento y mortalidad para edades y diversidades de clados usando enfoques ML o bayesianos. Ya conocemos la distribución de probabilidad completa para los modelos de nacimiento-muerte a partir de cualquier diversidad de pie N (0) = n ₀ (ver ecuaciones 10.13 y 10.15). Podemos usar estas ecuaciones para calcular la probabilidad de cualquier combinación particular de N y t (ya sea t _{s t e m} o t _{c r o w} n) dados valores particulares de λ y μ. Luego podemos encontrar valores de parámetros que maximicen esa probabilidad. Por supuesto, con datos de un solo clado, no podemos estimar parámetros de manera confiable; de hecho, estamos tratando de estimar dos parámetros a partir de un solo punto de datos, lo cual es un esfuerzo inútil. (Es común, en este caso, asumir algún nivel de extinción y calcular las tasas netas de diversificación con base en eso, como hicimos en el Cuadro 11.1 anterior).

También se puede suponer que un conjunto de clados tienen las mismas tasas de especiación y extinción y los ajustan simultáneamente, estimando los valores de los parámetros ML. Este es el enfoque adoptado por Magallón y Sanderson (2001) para calcular las tasas de diversificación entre angiospermas. Cuando aplicamos este enfoque a los datos de Páramo, mostrados anteriormente, obtenemos estimaciones ML de $\ hat {r} = 0.27$ y $\ hat {\ epsilon} = 0$. Si nos vemos obligados a estimar una tasa promedio general de especiación para todos estos clados, esta podría ser una estimación razonable. Sin embargo, la tabla anterior también sugiere que algunos de estos clados se están diversificando más rápido que otros. Volveremos al tema de la variación en las tasas de diversificación entre clados en el próximo capítulo.

También podemos usar un enfoque bayesiano para calcular las distribuciones posteriores para las tasas de nacimiento y mortalidad en función de las edades y diversidades de los clados. Este enfoque no se ha implementado, que yo sepa, en ningún paquete de software, aunque el método es sencillo (para un enfoque relacionado, ver Höhna et al. 2016). Para ello, modificaremos el algoritmo básico para MCMC bayesiano (ver Capítulo 2) de la siguiente manera.

Nota

1. Muestrear un conjunto de valores de parámetros iniciales, r y, a partir de sus distribuciones anteriores. Para este ejemplo, podemos establecer nuestra distribución anterior para ambos parámetros como exponencial con una media y varianza de λ _{p r i o r} (tenga en cuenta que su elección para este parámetro debe depender de las unidades que esté usando, especialmente para r). Luego seleccionamos a partir r y de sus antecedentes.

2. Dados los valores actuales de los parámetros, seleccione nuevos valores de parámetros propuestos utilizando la densidad propuesta Q (p ′| p). Para ambos valores de parámetro, podemos usar una densidad de propuesta uniforme con ancho w _p, de modo que Q (p ′| p) U (p − w _p /2, p + w p /2). Podemos elegir ambos valores de parámetros simultáneamente, o uno a la vez (este último suele ser más efectivo).

3. Calcula tres proporciones:
   • a. El ratio de probabilidades anterior. Esta es la relación de la probabilidad de dibujar los valores de los parámetros p y p′ del anterior. Como tenemos priores exponenciales para ambos parámetros, podemos calcular esta relación como:\ [R_ {prior} =\ frac {\ lambda_ {prior} e^ {-\ lambda_ {prior} p'}} {\ lambda_ {prior} e^ {-\ lambda_ {prior} p}} =e^ {\ lambda_ {prior} (p-p')}\ label 11.5}\ [

• b. La relación de densidad propuesta. Esta es la relación de probabilidad de propuestas que van de p a p ′ y a la inversa. Ya hemos declarado una densidad simétrica de propuesta, de manera que Q (p ′| p) = Q (p | p ′) y R _{p r o p o s a} l = 1.
• c. La razón de verosimilitud. Esta es la relación de probabilidades de los datos dados los dos valores de parámetros diferentes. Podemos calcular estas probabilidades a partir de las ecuaciones 10.13 o 10.16 (dependiendo de si los datos son edades del tallo o edades de la corona).

4. Encuentre R _{a c c e p t} como el producto de las probabilidades previas, la relación de densidad propuesta y la razón de verosimilitud. En este caso, la relación de densidad propuesta es 1, por lo que (eq. 11.6):

   R _{a c c e p t} = R _{p r i o r} ⋅ R _{l i k e l i h o o d}