12.2: Variación en las tasas de diversificación entre clados

Sabemos por análisis del equilibrio de árboles que el árbol de la vida está más desequilibrado de lo que predicen los modelos de nacimiento-muerte. Podemos explorar esta variación en las tasas de diversificación permitiendo que los modelos de nacimiento y muerte varíen a lo largo de ramas en árboles filogenéticos. El escenario más simple es cuando se tiene una predicción particular sobre las tasas de diversificación para probar. Por ejemplo, podríamos preguntarnos si las tasas de diversificación en un clado (clado A en la Figura 12.2) son mayores que en el resto del árbol filogenético. Podemos probar esta hipótesis ajustando un modelo de nacimiento-muerte de tasa múltiple.

El método más sencillo para llevar a cabo esta prueba es mediante el uso de la selección de modelos en un marco ML (Rabosky et al. 2007). Para ello, primero ajustamos un modelo de tasas constantes de nacimiento-muerte a todo el árbol y calculamos una probabilidad. Luego podemos ajustar los modelos de tasas variables de nacimiento-muerte a los datos, comparando el ajuste de estos modelos usando pruebas de razón de verosimilitud o A I C _C. La forma más sencilla de ajustar un modelo de tasas variables es adaptar la fórmula de verosimilitud en la ecuación 11.18 (o eq. 11.24 si las especies no están muestreadas). Calculamos la probabilidad en dos partes, una para la parte de fondo del árbol (con tasas λ _B y μ _B) y otra para el clado focal que puede tener diferentes dinámicas de diversificación (con tasas λ A y μ _A). Luego podemos comparar este modelo con uno en el que las tasas de especiación y extinción son constantes a través del tiempo.

Figura 12.2. Un árbol filogenético que incluye tres clados, que ilustra dos modelos posibles de diversificación: un modelo de tasas constantes, donde los tres clados tienen los mismos parámetros de diversificación λ _T y μ _T, y un modelo de tasas variables, donde el clado A tiene parámetros (λ _A y μ _A) que difieren de los otros dos clados (λ _B y μ _B). Imagen del autor, puede ser reutilizada bajo licencia CC-BY-4.0.

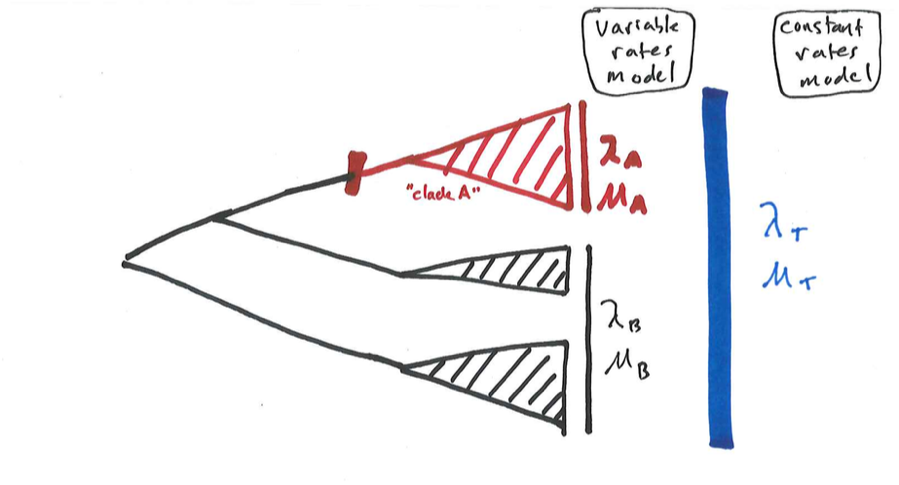
Consideremos el ejemplo de la Figura 12.2. Nos gustaría saber si el clado A tiene tasas de especiación y extinción, λ _A y μ _A, que difieren de las tasas de fondo, λ _B y μ _B — nosotros llamará a esto un modelo de “tarifas variables”. La alternativa es un modelo de “tasas constantes” donde todo el clado tiene parámetros de velocidad constante λ _T y μ _T. Estos dos modelos están anidados, ya que el modelo de tasas constantes es un caso especial del modelo de tasas variables donde λ _T = λ _A = λ _B y μ _T = μ _A = μ _B. Calcular la probabilidad para estos dos modelos es razonablemente sencillo: simplemente calculamos la probabilidad para cada sección del árbol usando la ecuación relevante del Capítulo 11, y luego multiplicamos las probabilidades de las dos partes del árbol (o agregamos las probabilidades logarítmicas) para obtener la probabilidad general.

Para un ejemplo real, veamos el árbol filogenético de los anfibios y evaluemos la hipótesis de que las ranas de cola y de Nueva Zelanda, clado hermano al resto de ranas, se diversificaron a un ritmo más lento que otros anfibios (Figura 12.3). Podemos utilizar el árbol filogenético “backbone” de Jetz y Pyron (Jetz y Pyron 2018), asignando diversidades en función de la clasificación asociada a dicha publicación. Luego podemos calcular probabilidades con base en la Ecuación 11.24.

Figura 12.3. Árbol filogenético de anfibios con tiempos de divergencia y diversidades de clados mayores. Datos de Jetz y Pyron (Jetz y Pyron 2018). Imagen del autor, puede ser reutilizada bajo licencia CC-BY-4.0.

Podemos calcular la probabilidad del modelo de tasas constantes, con dos parámetros λ _T y μ _T, a un modelo de tasas variables con cuatro parámetros λ _{l i o p} , μ _{l i o p}, λ _{o t h e r}, y μ _{o t h e} r. Para este ejemplo, obtenemos los siguientes resultados.

Modelo	Estimaciones de parámetros	Probabilidad LN	A I C c
Tasas constantes	λ T = 0.30	-1053.9	2111.8
	μ T = 0.28
Tasas variables	l a m b d a l i o p = 0.010	-1045.4	2101.1
	μ l i o p = 0.007
	l a m b d a o t h e r = 0.29
	μ o t h e r = 0.27

Con una diferencia en A I C _c de más de 10, vemos a partir de estos resultados que hay buenas razones para pensar que hay una diferencia en las tasas de diversificación en estas ranas “bichos raros” en comparación con el resto de los anfibios.

Por supuesto, son posibles comparaciones más elaboradas. Por ejemplo, se podría comparar el ajuste de cuatro modelos, de la siguiente manera: Modelo 1, tasas constantes; Modelo 2, tasa de especiación en el clado A difiere del fondo; Modelo 3, tasa de extinción en el clado A difiere del fondo; y Modelo 4, tanto las tasas de especiación como de extinción en el clado A difieren del fondo. En este caso, algunos de los pares de modelos están anidados —por ejemplo, el Modelo 1 es un caso especial del Modelo 2, que es, a su vez, un caso especial del Modelo 4— pero los cuatro no hacen una serie anidada. Aquí nos beneficiamos de utilizar un enfoque de selección de modelos basado en A I C _C. Podemos ajustar los cuatro modelos y usar su número relativo de parámetros para calcular las puntuaciones A I _{C C.} Luego podemos calcular pesos A I C _C para evaluar el soporte relativo para cada uno de estos cuatro modelos. (Como un aparte, ¡podría ser difícil diferenciar entre estas cuatro posibilidades sin muchos datos!)

Pero, ¿y si no tienes una razón a priori para predecir tasas diferenciales de diversificación entre clados? O bien, ¿y si la única razón por la que crees que un clado podría tener una tasa de diversificación diferente a otro es que tiene más especies? (¡Tal razonamiento es circular, y causará estragos con tus análisis!) En tales casos, podemos usar métodos que nos permitan ajustar modelos generales donde las tasas de diversificación pueden variar según los clados del árbol. Los métodos disponibles utilizan AIC paso a paso (MEDUSA, Alfaro et al. 2009; pero ver mayo y Moore 2016), o MCMC bayesiano de salto reversible (Rabosky 2014, 2017; pero ver Moore et al. 2016).

Por ejemplo, ejecutar un algoritmo Stepwise-AIC sobre los datos de anfibios (Alfaro et al. 2009) da como resultado un modelo con 11 regímenes diferentes de especiación y extinción (Figura 12.4). Esta es una buena evidencia de que las tasas de diversificación han variado enormemente a lo largo de la historia de los anfibios.

Figura 12.4. Análisis de cambios de tasa de diversificación entre clados de anfibios usando MEDUSA (Alfaro et al. 2009). Las flechas resaltan los lugares donde se deduce que la especiación, extinción o ambas han cambiado; las flechas verdes indican un aumento inferido en r = λ − μ, mientras que las flechas rojas indican disminución de r. Datos de Jetz y Pyron (Jetz y Pyron 2018). Imagen del autor, puede ser reutilizada bajo licencia CC-BY-4.0.

Una nota: todos los enfoques actuales se ajustan a un modelo donde las tasas de nacimiento y mortalidad cambian en momentos discretos en el árbol filogenético, es decir, a lo largo de ciertas ramas del árbol que conducen a los taxones existentes. Uno podría desear un enfoque, entonces, que modele tales cambios -usando, por ejemplo, un proceso de Poisson- y luego localice los cambios en el árbol. Sin embargo, aún nos faltan las matemáticas para resolver para E (t) (por ejemplo, Ecuación 11.19) bajo tal modelo (Moore et al. 2016). Dado eso, podemos ver las implementaciones actuales de modelos donde las tasas varían entre clados como una aproximación a la probabilidad, y uno que descuenta la posibilidad de cambios en las tasas de especiación y/o extinción entre los clados que no sobrevivieron hasta nuestros días (Rabosky 2017) - ¡y estamos atrapados con eso hasta que se desarrolle una mejor alternativa!