Saltar al contenido principal
LibreTexts Español

1.7: Probabilidades en genética

  1. Última actualización
  2. Guardar como PDF
  • Page ID
    57561

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

    Introducción

    El cuadrado Punnett es una herramienta valiosa, pero no es ideal para todos los problemas genéticos. Por ejemplo, supongamos que se le pidió que calculara la frecuencia de la clase recesiva no para una cruz de Aa x Aa, no para una cruz de AAbb x AAbb, sino para una cruz de AabbcCDDee x AabbcCDDee. Si quisieras resolver esa pregunta usando un cuadrado Punnett, podrías hacerlo, pero tendrías que completar un cuadrado Punnett con 1024 cajas. Probablemente no lo que quieras dibujar durante un examen, o en cualquier otro momento, ¡si puedes evitarlo!

    El problema de cinco genes anterior se vuelve menos intimidante una vez que te das cuenta de que un cuadrado de Punnett es solo una forma visual de representar los cálculos de probabilidad. Aunque es una gran herramienta cuando se trabaja con uno o dos genes, puede volverse lento y engorroso a medida que aumenta el número. En algún momento, se vuelve más rápido (y menos propenso a errores) simplemente hacer los cálculos de probabilidad por sí mismos, sin la representación visual de un cuadrado torpe de Punnett. En todos los casos, los cálculos y el cuadrado proporcionan la misma información, pero al tener ambas herramientas en su cinturón, puede estar preparado para manejar una gama más amplia de problemas de una manera más eficiente.

    En este artículo, revisaremos algunos conceptos básicos de probabilidad, incluyendo cómo calcular la probabilidad de que ocurran dos eventos independientes (evento X e Y) o la probabilidad de que ocurra uno de dos eventos mutuamente excluyentes (evento X o evento Y). Luego veremos cómo estos cálculos se pueden aplicar a problemas genéticos, y, en particular, cómo pueden ayudarte a resolver problemas que involucran números relativamente grandes de genes.

    [Solución al problema cruzado de cinco genes]

    En este problema, se supone que debemos encontrar la frecuencia de la clase recesiva entre la descendencia de una cruz aabbccddee x aabbccddee, es decir, la frecuencia de individuos aabbccddee. ¿Cómo conseguimos un individuo aabbccddee? Solo hay una manera de que eso suceda: ambos padres deben aportar un gameto abcde.

    ¿Cuál es entonces la probabilidad de que uno de los padres haga un gamete abcde? Ambos padres son heterocigotos para los cinco genes, por lo que hay una 1/2 probabilidad de obtener el alelo recesivo (minúscula) para cualquier gen. Para obtener nuestro gameto deseado, necesitamos los cinco genes en forma recesiva (a y b y c y d y e). Este es un caso donde podemos aplicar la regla del producto, que establece que la probabilidad de que ocurra el evento X y el evento Y es producto de sus probabilidades individuales (probabilidad de X veces probabilidad de Y), asumiendo que X e Y son eventos independientes. Por lo tanto, la probabilidad general de que un padre produzca un gameto abcde es:

    Probabilidad de gameto abcde = (probabilidad de a) x (probabilidad de b) x (probabilidad de c) x (probabilidad de d) x (probabilidad de e)

    \(P(abcde)=P(a)\cdot P(b)\cdot P(c)\cdot P(d)\cdot P(e)\)

    \(P(abcde)=(1/2)\cdot (1/2)\cdot (1/2)\cdot (1/2)\cdot (1/2)=(1/2)^5=1/32\)

    Si esa es la probabilidad de que uno de los padres haga un gameto abcde, ¿cuál es la probabilidad de que ambos padres lo hagan? Nuevamente, podemos aplicar la regla “y” (regla del producto), ya que necesitamos tanto el padre 1 como el padre 2 para hacer un gameto abcde con el fin de obtener nuestro homocigoto recesivo objetivo. Así, la probabilidad general es:

    Probabilidad de aabbccddee individual = (probabilidad de que el padre 1 haga un gameto abcde) x (probabilidad de que el padre 2 haga un gameto abcde)

    \(P(aabbccddee)=P(abcde_\text{parent A})\cdot P(abcde_\text{parent B})\)

    \(P(aabbccddee)=(1/32)\cdot (1/32)=1/1024\)

    Esa es nuestra probabilidad general de un homocigoto recesivo para los cinco genes.

    La probabilidad 1/1024 corresponde a 1 caja de las 1024 casillas del cuadrado Punnett que tendrías que dibujar para representar esta cruz. El cálculo de probabilidad es el mismo cálculo que haríamos implícitamente dibujando el cuadrado de Punnett, solo más rápido y con menos posibilidades de errores.

    Conceptos básicos de probabilidad

    Las probabilidades son medidas matemáticas de verosimilitud. En otras palabras, son una forma de cuantificar (dar un valor numérico específico a) la probabilidad de que algo suceda. Una probabilidad de 1 para un evento significa que se garantiza que suceda, mientras que una probabilidad de 0 para un evento significa que se garantiza que no suceda. Un simple ejemplo de probabilidad es tener una probabilidad 1/2 de conseguir cabezas cuando se lanza una moneda, como explica Sal en este video de introducción a la probabilidad.

    Las probabilidades pueden ser empíricas, es decir, que se calculan a partir de observaciones de la vida real, o teóricas, lo que significa que se predicen usando un conjunto de reglas o suposiciones.

    • La probabilidad empírica de un evento se calcula contando el número de veces que ocurre ese evento y dividiéndolo por el número total de veces que ese evento pudo haber ocurrido. Por ejemplo, si el evento que estabas buscando fue una semilla de guisante arrugada, y la viste 1,850 veces de las 7,324 semillas totales que examinaste, la probabilidad empírica de obtener una semilla arrugada sería de 1,850/7,324 = 0.253, o muy cercana a 1 de cada 4 semillas.
    • La probabilidad teórica de un evento se calcula a partir de información sobre las reglas y circunstancias que producen el evento. Refleja el número de veces que se espera que ocurra un evento en relación con el número de veces que posiblemente podría ocurrir. Por ejemplo, si tuvieras una planta de guisante heterocigótica para un gen de forma de semilla (Rr) y dejaras que se autofecundara, podrías usar las reglas de probabilidad y tu conocimiento de la genética para predecir que 1 de cada 4 crías obtendría dos alelos recesivos (rr) y aparecería arrugada, correspondiente a una probabilidad de 0.25 (1/4). A continuación hablaremos más sobre cómo aplicar las reglas de probabilidad en este caso.

    En general, cuanto mayor sea el número de puntos de datos que se utilizan para calcular una probabilidad empírica, como las formas de semillas de guisante individuales, más se acercará a la probabilidad teórica.

    La regla del producto

    Una regla de probabilidad que es muy útil en genética es la regla del producto, que establece que la probabilidad de que dos (o más) eventos independientes ocurran juntos se puede calcular multiplicando las probabilidades individuales de los eventos. Por ejemplo, si rotas una vez un dado de seis lados, tienes 1/6 de posibilidades de conseguir un seis. Si lanzas dos dados a la vez, tu probabilidad de obtener dos seis es: (probabilidad de un seis en el dado 1) x (probabilidad de un seis en el dado 2) = (1/6) ⋅ (1/6) = 1/36.

    En general, puede pensar en la regla del producto como la regla “y”: si tanto el evento X como el evento Y deben ocurrir para que ocurra un determinado resultado, y si X e Y son independientes entre sí (no afectan la probabilidad del otro), entonces puede usar la regla del producto para calcular la probabilidad del resultado multiplicando las probabilidades de X e Y.

    Podemos usar la regla del producto para predecir frecuencias de eventos de fertilización. Por ejemplo, considere un cruce entre dos individuos heterocigotos (Aa). ¿Cuáles son las probabilidades de conseguir un aa individual en la próxima generación? La única manera de obtener un aa individual es si la madre aporta un a gameto y el padre aporta un a gameto. Cada padre tiene una probabilidad 1/2 de hacer un gameto. Así, la probabilidad de una descendencia aa es: (probabilidad de que la madre contribuya a) x (probabilidad de que el padre contribuya a) = (1/2) ⋅ (1/2) = 1/4.

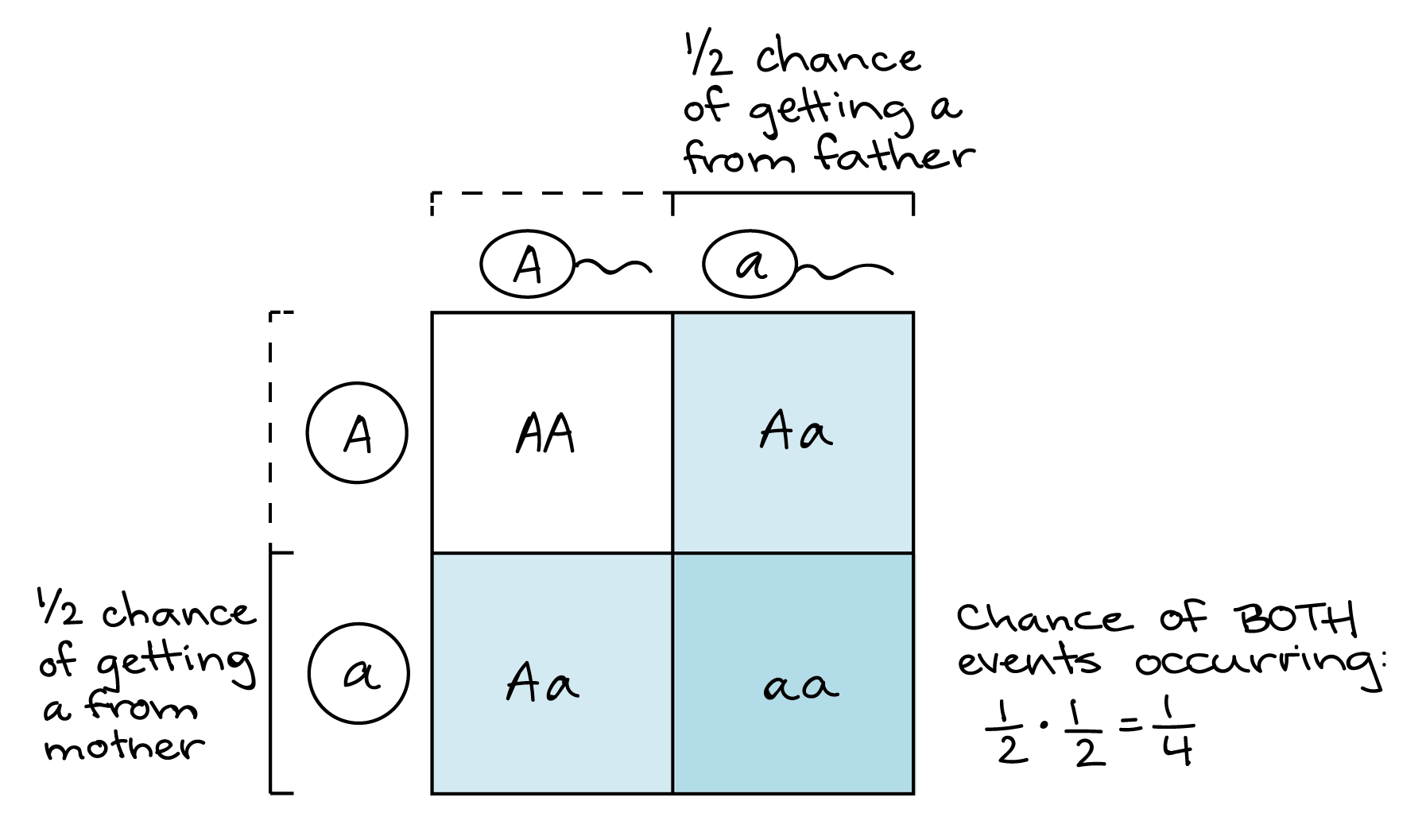
    Ilustración de cómo un cuadrado Punnett puede representar la regla del producto. Cuadrado Punnett: ||A|a-|-|-|-A||AA|**AA**A||_AA_|***AA*** Hay una 1/2 probabilidad de obtener un alelo a del progenitor masculino, correspondiente a la columna más a la derecha del cuadrado Punnett. De igual manera, hay una probabilidad de 1/2 de obtener un alelo a del padre materno, correspondiente a la fila más baja del cuadrado Punnett. El cruce de estos la fila y columna, correspondiente al cuadro inferior derecho de la tabla, representa la probabilidad de obtener un alelo del padre materno y del padre paterno (1 de cada 4 casillas en el cuadrado de Punnett, o una probabilidad de 1/4).

    Este es el mismo resultado que obtendrías con un cuadrado Punnett, y en realidad el mismo proceso lógico también, ¡algo que me llevó años darme cuenta! La única diferencia es que, en el cuadrado de Punnett, haríamos el cálculo visualmente: representaríamos la probabilidad 1/2 de un gameto de cada padre como una de cada dos columnas (para el padre) y una de cada dos filas (para la madre). La intersección de 1 cuadrado de la columna y la fila (de los 4 cuadrados totales de la tabla) representa la probabilidad de 1/4 de obtener una a de ambos padres.

    La regla de la suma de probabilidad

    En algunos problemas genéticos, es posible que deba calcular la probabilidad de que ocurra cualquiera de varios eventos. En este caso, deberás aplicar otra regla de probabilidad, la regla de suma. Según la regla de suma, la probabilidad de que ocurra cualquiera de varios eventos mutuamente excluyentes es igual a la suma de las probabilidades individuales de los eventos.

    Por ejemplo, si rotas un dado de seis caras, tienes una probabilidad de 1/6 de obtener cualquier número dado, pero solo puedes obtener un número por rollo. Nunca se podría obtener tanto un uno como un seis al mismo tiempo; estos resultados son mutuamente excluyentes. Así, las posibilidades de obtener ya sea un uno o un seis son: (probabilidad de obtener un 1) + (probabilidad de obtener un 6) = (1/6) + (1/6) = 1/3.

    Se puede pensar en la regla de suma como la regla “o”: si un resultado requiere que se produzca el evento X o el evento Y, y si X e Y son mutuamente excluyentes (si solo uno u otro puede ocurrir en un caso dado), entonces la probabilidad del resultado se puede calcular sumando las probabilidades de X e Y.

    Como ejemplo, usemos la regla de suma para predecir la fracción de descendencia de un cruce Aa x Aa que tendrá el fenotipo dominante (genotipo AA o Aa). En este cruce, hay tres eventos que pueden conducir a un fenotipo dominante:

    • Dos gametos A se encuentran (dando genotipo AA), o
    • Un gameto de mamá se encuentra con un gameto de papá (que le da el genotipo Aa), o
    • un gameto de Mom meets A gameto from Dad (dando genotipo Aa)

    En cualquier evento de fertilización, solo puede ocurrir una de estas tres posibilidades (son mutuamente excluyentes).

    Dado que se trata de una situación “o” en la que los hechos son mutuamente excluyentes, podemos aplicar la regla de la suma. Usando la regla del producto como hicimos anteriormente, podemos encontrar que cada evento individual tiene una probabilidad de 1/4. Entonces, la probabilidad de descendencia con un fenotipo dominante es: (probabilidad de A de mamá y A de papá) + (probabilidad de A de mamá y a de papá) + (probabilidad de a de mamá y A de papá) = (1/4) + (1/4) + (1/4) = 3/4.

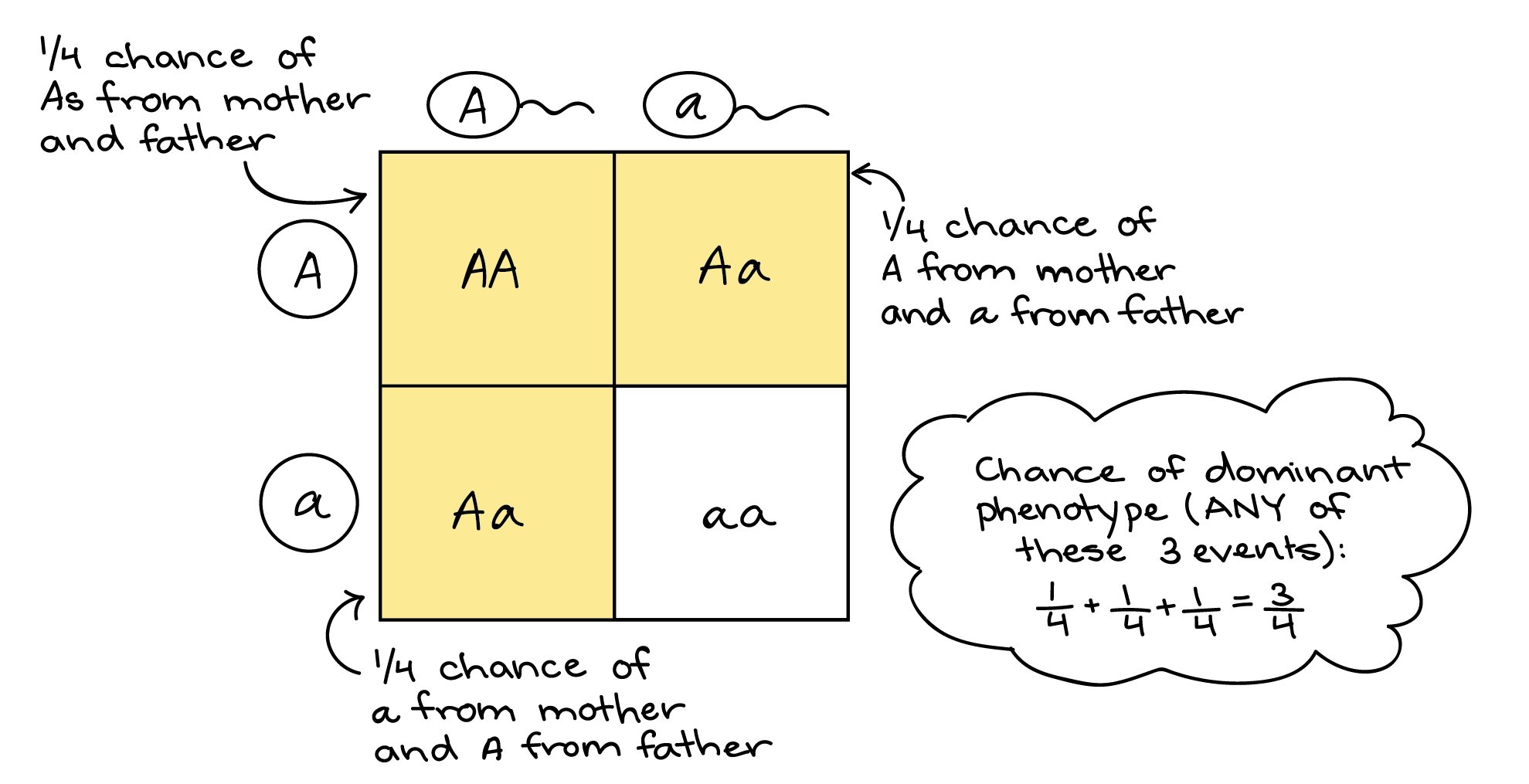
    Ilustración de cómo un cuadrado de Punnett puede representar la regla de suma. Cuadrado de Punnett: ||A|a-|-|-|-A|**AA**|**AA**A||**AA**|AA Las casillas **en negrita** representan eventos que dan como resultado un fenotipo dominante (genotipo AA o Aa). En uno, un espermatozoide A se combina con un óvulo A. En otro, un espermatozoide A se combina con un óvulo, y en un tercio, un espermatozoide se combina con un óvulo A. Cada evento tiene una probabilidad de 1/4 de suceder (1 de cada 4 cajas en la plaza Punnett). La probabilidad de que ocurra cualquiera de estos tres eventos es de 1/4+1/4+1/4 = 3/4.

    Una vez más, este es el mismo resultado que obtendríamos con un cuadrado Punnett. Una de las cuatro cajas de la plaza Punnett contiene el homocigoto dominante, AA. Dos cajas más representan heterocigotos, una con una A materna y una paterna, la otra con la combinación opuesta. Cada caja es 1 de las 4 cajas en todo el cuadrado Punnett, y como las cajas no se superponen (son mutuamente excluyentes), podemos sumarlas (1/4 + 1/4 + 1/4 = 3/4) para obtener la probabilidad de descendencia con el fenotipo dominante.

    La regla del producto y la regla de la suma

    Regla del producto Regla de suma
    Para eventos independientes X e Y, la probabilidad (\(P\)) de que ambos ocurran (X e Y) es\(P(X)\cdot P(Y)\). Para eventos mutuamente excluyentes X e Y, la probabilidad (\(P\)) de que uno ocurra (X o Y) es\(P(X)+P(Y)\).

    Aplicación de reglas de probabilidad a cruces dihíbridos

    El cálculo directo de probabilidades no tiene mucha ventaja sobre los cuadrados de Punnett para escenarios de herencia de un solo gen. (De hecho, si prefieres aprender visualmente, puedes encontrar el cálculo directo más difícil que más fácil). Donde las probabilidades brillan, sin embargo, es cuando estás mirando el comportamiento de dos, o incluso más, genes.

    Por ejemplo, imaginemos que criamos dos perros con el genotipo BBcc, donde el alelo dominante B especifica el color del pelaje negro (versus b, color de pelaje amarillo) y el alelo dominante C especifica pelaje recto (versus c, pelaje rizado). Suponiendo que los dos genes se agrupan de forma independiente y no están vinculados al sexo, ¿cómo podemos predecir el número de cachorros bbCC entre las crías?

    Un enfoque es dibujar un cuadrado Punnett de 16 cuadrados. Para un cruce que involucra a dos genes, un cuadrado Punnett sigue siendo una buena estrategia. Alternativamente, podemos usar una técnica de atajo que involucra cuadrados Punnett de cuatro cuadrados y una pequeña aplicación de la regla del producto. En esta técnica, dividimos la pregunta general en dos preguntas más pequeñas, cada una relacionada con un evento genético diferente:

    1. ¿Cuál es la probabilidad de obtener un genotipo Bb?
    2. ¿Cuál es la probabilidad de obtener un genotipo Cc?

    Para que un cachorro tenga un genotipo BBcc, ambos eventos deben tener lugar: el cachorro debe recibir alelos Bb, y debe recibir alelos Cc. Los dos eventos son independientes porque los genes se asumen de forma independiente (no afectan la herencia del otro). Entonces, una vez calculamos la probabilidad de cada evento genético, podemos multiplicar estas probabilidades usando la regla del producto para obtener la probabilidad del genotipo de interés (BBcc).

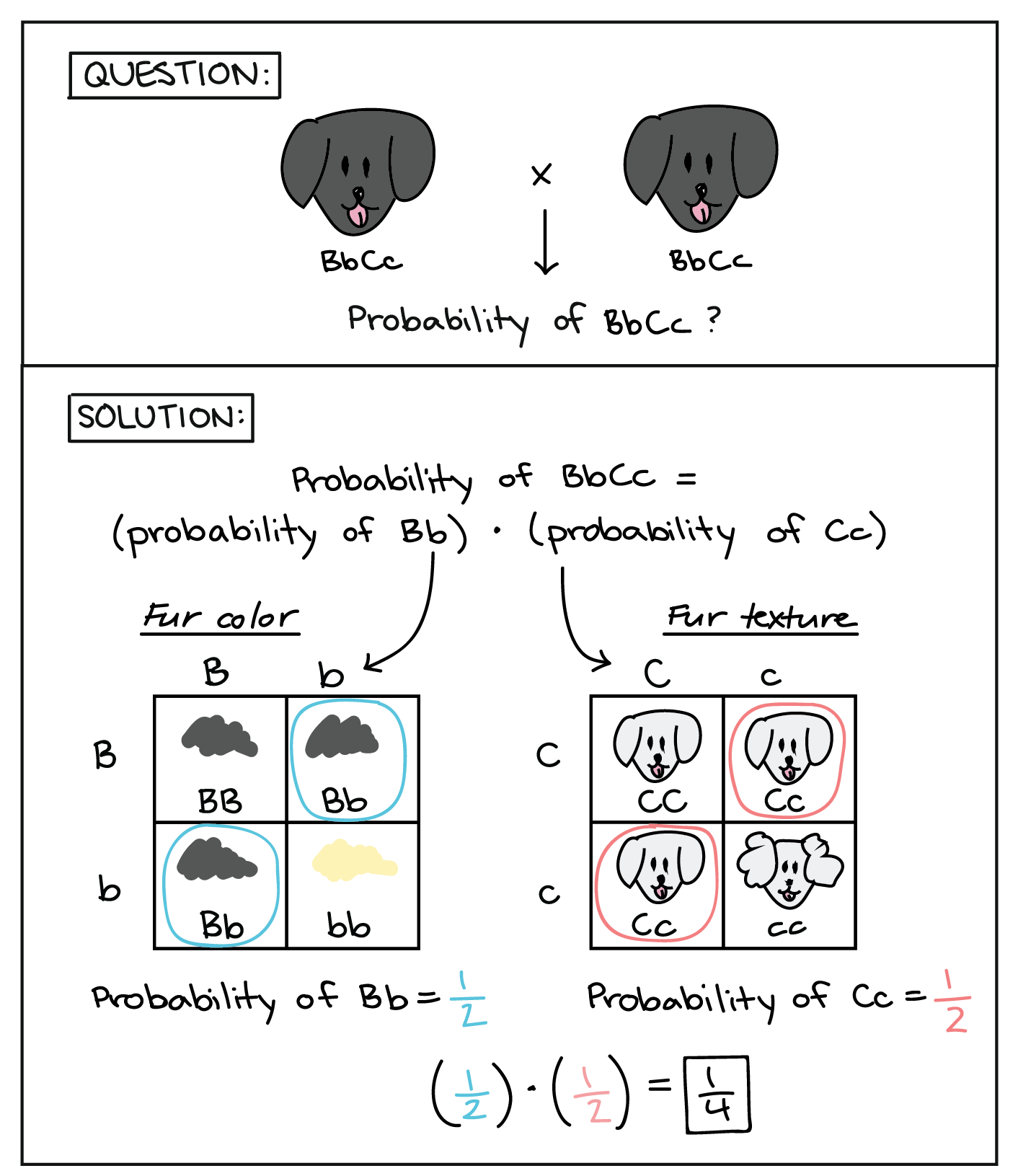
    Diagrama que ilustra cómo se pueden usar cuadrados Punnett 2X2 junto con la regla del producto para determinar la probabilidad de un genotipo particular en un cruce dihíbrido. Panel superior: Pregunta: cuando se cruzan dos perros BBCC, ¿cuál es la probabilidad de obtener un individuo de descendencia BBCC? Panel inferior: Solución: probabilidad de BBcc = (probabilidad de Bb) x (probabilidad de Cc). Cuadrado Punnett para color de pelaje: ||B|B-|-|-|-B||BB|**BB**b||**bb**|BB Probabilidad de genotipo Bb: 1/2. Cuadrado Punnett para textura de pelaje: ||C|C-|-|-|-C||CC|**CC**C||**CC**|CC Probabilidad de genotipo Cc: 1/2. Probabilidad de BBcc = (probabilidad de Bb) x (probabilidad de Cc). Probabilidad de BBcc = (1/2) x (1/2) = 1/4

    Para calcular la probabilidad de obtener un genotipo Bb, podemos dibujar un cuadrado Punnett de 4 cuadrados usando los alelos de los padres solo para el gen del color del pelaje, como se muestra arriba. Usando el cuadrado Punnett, se puede ver que la probabilidad del genotipo Bb es 1/2. (Alternativamente, podríamos haber calculado la probabilidad de Bb usando la regla de producto para las contribuciones de gameto de los dos padres y la regla de suma para las dos combinaciones de gametos que dan Bb.) Usando un cuadrado Punnett similar para los alelos de textura de pelaje de los padres, la probabilidad de obtener un genotipo Cc también es 1/2. Para obtener la probabilidad general del genotipo bbCC, simplemente podemos multiplicar las dos probabilidades, dando una probabilidad general de 1/4.

    [Comprobemos eso con un cuadrado Punnett]

    Cuadrado Punnett de 16 cuadrados que ilustra la misma solución alcanzada usando el método de probabilidad. ||BC|BC|BC|BC-|-|-|-|-|-|-BC||BBCC|BBCC|BBCC|**BBCC**BC||BBCC|BBCC|**BBCC||BBCC||BBCC|**BBCC**|BBCC|BBCC|BBCCBC||**BBCC|BBCC|BBCC|BBCC|BBCC Fracción de progenie de **BBCC** tipo: 4/16 = 1/4

    También se puede utilizar esta técnica para predecir frecuencias de fenotipos. ¡Pruébalo en la pregunta de práctica a continuación!

    Verifica tu comprensión

    Consulta\(\PageIndex{1}\)

    [Pista]

    Podemos desglosar la pregunta en dos preguntas más pequeñas:

    1. ¿Qué fracción de descendencia tendrá color de pelaje negro?
    2. ¿Qué fracción de descendencia tendrá pelaje recto?

    Dado que el color del pelaje negro y el pelaje recto son rasgos dominantes, todos los cachorros BB y Bb tendrán abrigos negros, y todos los cachorros CC y Cc tendrán pelaje recto, correspondiente a 3/4 de cachorros en cada caso. (Puede dibujar los cuadrados individuales de Punnett para los genes de color y textura para confirmar estas frecuencias).

    Para obtener la probabilidad de que un cachorro tenga tanto el color del pelaje negro como el pelaje recto, puedes multiplicar las probabilidades de estos dos eventos independientes:\((3/4)\cdot(3/4)=9/16\).

    9/16 de los cachorros tendrán abrigos negros y pelaje recto.

    Más allá de los cruces dihíbridos

    El método de probabilidad es más poderoso (y útil) en casos que involucran un gran número de genes.

    Por ejemplo, imagina un cruce entre dos individuos con varios alelos de cuatro genes no enlazados: aabbccdd x aabbccdd. Supongamos que quería averiguar la probabilidad de tener descendencia con el fenotipo dominante para los cuatro rasgos. Afortunadamente, se puede aplicar exactamente la misma lógica que en el caso de los cruces dihíbridos anteriores. Para tener el fenotipo dominante para los cuatro rasgos, y el organismo debe tener: una o más copias del alelo dominante A y una o más copias del alelo dominante B y una o más copias del alelo dominante C y una o más copias del alelo dominante C y una o más copias del alelo dominante D.

    Dado que los genes están desvinculados, estos son cuatro eventos independientes, por lo que podemos calcular una probabilidad para cada uno y luego multiplicar las probabilidades para obtener la probabilidad del resultado general.

    • La probabilidad de obtener una o más copias del alelo A dominante es de 3/4. (Dibuja un cuadrado Punnett para Aa x Aa para confirmar por ti mismo que 3 de las 4 casillas son AA o Aa.)
    • La probabilidad de obtener una o más copias del alelo B dominante es 1/2. (Dibuja un cuadrado Punnett para Bb x bb: encontrarás que la mitad de la descendencia son Bb, y la otra mitad bb.)
    • La probabilidad de obtener una o más copias del alelo C dominante es 1. (Si uno de los padres es homocigoto CC, ¡no hay manera de obtener descendencia sin un alelo C!)
    • La probabilidad de obtener una o más copias del alelo D dominante es 1/2, en cuanto a B. (La mitad de la descendencia será Dd, y la otra mitad será dd.)

    Para obtener la probabilidad general de descendencia con el fenotipo dominante para los cuatro genes, podemos multiplicar las probabilidades de los cuatro eventos independientes:\((3/4)\cdot(1/2)\cdot(1)\cdot(1/2)=3/16\).

    Verifica tu comprensión

    Consulta\(\PageIndex{2}\)

    [Pista]

    No es posible sacar de esta cruz a un individuo cuádruple homocigótico recesivo. Eso es porque la probabilidad de obtener dos alelos c recesivos es cero. El primer progenitor solo tiene alelos dominantes para este gen, asegurando que cada una de las crías recibirá al menos un alelo C dominante (y así no puede mostrar el fenotipo recesivo).

    ¿Cómo figura matemáticamente la probabilidad cero de un genotipo cc? Para obtener la probabilidad general del genotipo aabbccdd, tendríamos que multiplicar las probabilidades de los genotipos deseados para los otros tres genes (aa, 1/4; bb, 1/2; y dd, 1/2) por el cero correspondiente al genotipo cc, dando un probabilidad de cero.

    \(P(aabbccdd)=P(aa) \cdot P(bb) \cdot P(cc) \cdot P(dd)\)

    \(P(aabbccdd)=(1/4)\cdot(1/2)\cdot(0)\cdot(1/2)=0\)

    La probabilidad de obtener un individuo con un fenotipo recesivo para los cuatro genes es 0.

    Colaboradores y Atribuciones

    [Atribución y referencias]

    Atribución:

    Este artículo es un derivado modificado de los siguientes artículos:

    El artículo modificado está licenciado bajo una licencia CC BY-NC-SA 4.0.

    Referencias adicionales:

    Griffiths, A. J. F., Miller, J. H., Suzuki, D. T., Lewontin, R. C., y Gelbart, W. M. (2000). Usando proporciones genéticas. En Una introducción al análisis genético (7a ed.). Nueva York, NY: W. H. Freeman. Recuperado de http://www.ncbi.nlm.nih.gov/books/NBK21812/.

    Purves, W. K., Sadava, D., Orians, G. H., y Heller, H. C. (2003). Cuadrados de Punnett o cálculos de probabilidad: Una elección de métodos. En la vida: La ciencia de la biología (7ª ed., pp. 195-196). Sunderland, MA: Asociados Sinauer.

    Reece, J. B., Urry, L. A., Caín, M. L., Wasserman, S. A., Minorsky, P. V., y Jackson, R. B. (2011). Mendel y la idea genética. En Campbell Biology (10a ed., pp. 267-291). San Francisco, CA: Pearson.

    Raven, P. H., Johnson, G. B., Mason, K. A., Losos, J. B., y Singer, S. R. (2014). Patrones de herencia. En Biología (10a ed., AP ed., pp. 221-238). Nueva York, NY: McGraw-Hill.

    Staroscik, A. (2015). Calculadora cuadrada Punnett. En Scienceprimer.com. Recuperado de http://scienceprimer.com/punnett-square-calculator.

    El Proyecto Adapa. (2014, 13 de agosto). ¿Cuáles son las leyes de segregación y surtido independiente y por qué son tan importantes? En BioBook. Recuperado de https://adapaproject.org/bbk_temp/tiki-index.php?page=Leaf%3A+What+are+the+laws+of+segregation+and+independent+assortment+and+why+are+they+so+important%3F.

    1.7: Probabilidades en genética is shared under a CC BY-NC-SA 3.0 license and was authored, remixed, and/or curated by LibreTexts.