5.16: El Modelo Factor Específico

Objetivos de aprendizaje

1. Conocer los supuestos detallados del modelo factorial específico.
2. Aprende cómo los cambios de precios afectan los salarios, alquileres y rendimientos de factores usando el diagrama de Mussa.
3. Aprende los efectos del libre comercio sobre el salario real y la renta real en un modelo factorial específico.

Considera una economía con dos industrias perfectamente competitivas, la textil y el acero. Supongamos que la salida de ambos productos requiere mano de obra y capital como insumos de factor. Sin embargo, imaginaremos que el capital utilizado en la producción textil consiste en equipos como telares, mientras que el capital utilizado en la producción de acero requiere equipos como altos hornos. Dado que cada tipo de capital está diseñado para su uso en un proceso de producción específico, lo llamamos “capital específico”. Podemos imaginar que si el capital de una industria se desplazara a otra, su productividad en la nueva industria sería cero. Simplemente imagina la utilidad de un alto horno en la producción textil y ¡deberías ver el punto! Así, para que el capital permanezca plenamente empleado, debe permanecer en la misma industria, es inmóvil, o atascado en su respectiva industria.

Asumimos que el trabajo, por otro lado, es homogéneo y perfectamente móvil libremente entre las dos industrias. Esto implicará que el problema de elección de una firma se reduce a la decisión de cuánta mano de obra contratar y cuánto producir para maximizar sus ganancias, dado que tiene una cantidad fija de capital disponible para usar. Asumiremos por simplicidad que el capital social en cada industria está exógenamente fijo y no hay inversión en nuevo capital.

Equilibrio de una sola empresa en el modelo de factor específico

En este contexto, una empresa maximizará sus ganancias cuando produzca un nivel de producción tal que el salario que debe pagar a los trabajadores sea igual al valor del producto marginal en el nivel de producción elegido. Esto está escrito en forma de ecuación para una firma textil de la siguiente manera:

\[ w = P_T MP_T \nonumber .\]

El lado izquierdo de la ecuación representa el salario por hora que la firma paga a sus trabajadores. El lado derecho es el valor del producto marginal, que consiste en el producto del precio de mercado de la producción (\(P_T\)) y el producto marginal de producción (\(MP_T\)). El producto marginal, a su vez, representa la salida adicional que se puede obtener al aumentar el insumo de mano de obra en una unidad. Por ejemplo, si\(MP_T = 10\), esto significa que al agregar una hora más de mano de obra, se podrían producir diez metros adicionales de tela. Las unidades de la expresión\(MP_T\) son metros de tela por hora de trabajo (m/hr.). Cuando se multiplica por el precio, medido como dólares por metro, el producto,\(P_T MP_T\), arroja el número de dólares que podrían ganarse por hora de mano de obra adicional aplicada en la producción. Esta es entonces la definición del valor del producto marginal en este contexto. Se mide en dólares por hora, lo mismo que se mide el salario, ¡algo bueno ya que deben ser iguales entre sí!

Para ver por qué esta condición se mantendrá cuando la firma maximice el beneficio, graficaremos estas expresiones en la Figura\(\PageIndex{1}\), que representa el valor de una línea marginal de productos para una firma textil representativa\(VMP_T = P_T MP_T\), y la tasa salarial del mercado\(w_T\),, con respecto a la oferta laboral.

Se supone que el salario es exógeno para cada empresa y es independiente de la oferta laboral. De ahí que se dibuje como una línea horizontal a nivel del salario,\(w_T\). Posteriormente el salario se determinará endógenamente a través de la interacción de las dos industrias. Sin embargo, las empresas de ambas industrias reconocen que son demasiado pequeñas para influir en el salario del mercado y tomar decisiones basadas en un salario exógenamente dado.

Figura\(\PageIndex{1}\): Modelo de factor específico—equilibrio de una sola empresa

El valor del producto marginal es una función decreciente del trabajo. Esto significa que a niveles más altos de uso de mano de obra, cada unidad adicional de mano de obra aplicada a la producción agrega menos unidades de producción. La intuición para esto es sencilla. Imagine que cada vez más trabajadores son asignados para usar la misma máquina en un proceso de producción. Cada trabajador adicional puede ayudar en el proceso de producción y agregar salida (así\(MP > 0\)), pero a medida que se agreguen más y más, el hacinamiento se establecerá y cada persona encontrará cada vez menos que hacer eso es útil. Así caerá el producto marginal. Dado que dibujamos el valor de la línea marginal de productos bajo el supuesto de que hay una cantidad fija de capital específico en la industria, el mismo argumento de hacinamiento se aplica a la mayor escala de la industria.

La posición de la\(VMP\) línea depende del precio de mercado y de la cantidad de capital específico, ambos asumidos como exógenos. Si el precio del producto sube (baja), la\(VMP\) línea se desplaza hacia arriba (a la baja). Lo mismo se aplica para los cambios en la cantidad de capital específico. Si la cantidad de capital específico en la industria subiera (bajara), la\(VMP\) línea se desplazaría hacia arriba (a la baja).

La elección maximizadora de beneficios del insumo laboral por parte de la industria se determina a nivel\(LE\) en el eje horizontal, donde el salario\(w_T\) es igual al valor del producto marginal\(VMP_T\) en el punto\(E\). Para ver por qué, considere lo que significaría si la industria eligiera un insumo laboral diferente, digamos\(L1\). En\(L1\),\(VMP_{L1} > w_T\). Esto dice que los ingresos adicionales obtenidos al ampliar la entrada de mano de obra por una unidad superan el costo adicional de agregar una unidad más de mano de obra. Por lo tanto, agregar una unidad más de trabajo debe generar ganancias, lo que significa que esa\(L1\) no puede ser la opción maximizadora de ganancias, debe mentir a la derecha de\(L1\). A continuación considere el insumo laboral\(L2\). En\(L2\),\(VMP_{L2} < w_T\). Esto dice que los ingresos adicionales que se obtienen al ampliar la entrada de mano de obra por una unidad son menores que el costo de agregar una unidad más de mano de obra. Por lo tanto, agregar una unidad más de trabajo debe disminuir el beneficio, lo que significa que esa\(L2\) no puede ser la opción maximizadora de ganancias, debe estar a la izquierda de\(L2\). Por último, considere el aporte laboral\(LE\). En\(LE\),\(VMP_{LE} = w_T\). Esto dice que los ingresos adicionales obtenidos al ampliar la entrada de mano de obra por una unidad equivalen al costo adicional de agregar una unidad más de mano de obra. Por lo tanto, agregar una unidad más de trabajo no tiene efecto sobre el beneficio, lo que significa que esa\(LE\) debe ser la opción maximizadora de ganancias.

Pagos por factores

En la Figura\(\PageIndex{2}\), consideramos formas de representar los pagos de factores realizados en un equilibrio. Considerar una tasa salarial\(w_T\) y un aporte laboral de equilibrio dado por\(LE\). El producto de estos dos,\(w_TLE\), representa la cantidad total de dinero que se debe pagar a los trabajadores de la industria y se le conoce como la factura salarial. Son los cargos en los que incurren los propietarios (es decir, la factura que debe pagarse) para contratar a los trabajadores. Está representado por el área sombreada verde.

Figura\(\PageIndex{2}\): Modelo de factor específico—pagos de factores

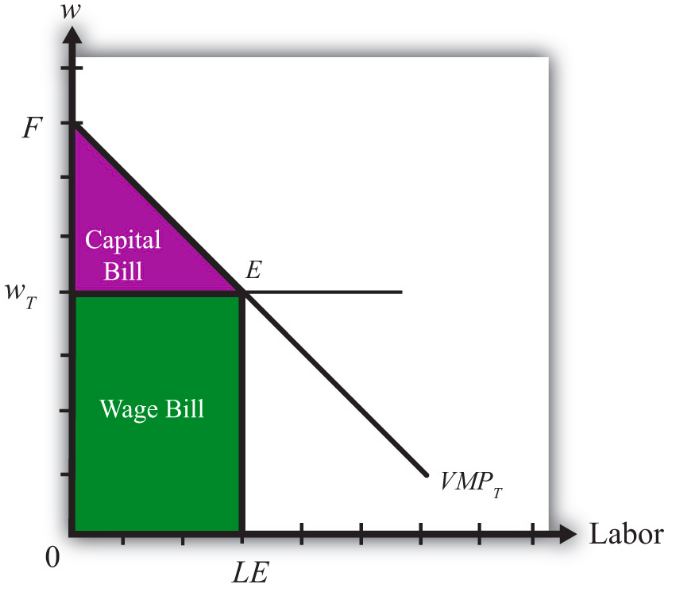
El monto total de ingresos obtenidos por la firma en el mercado viene dado por el área total sombreada (verde + morado). Esto corresponde al área bajo la\(VMP_T\) línea entre\(0\) y\(LE\) unidades de trabajo. Sin el uso del cálculo, es difícil describir por qué esto es así. Sin embargo, dado que el\(VMP\) da los ingresos adicionales obtenidos por cada unidad de trabajo adicional, uno puede imaginar comenzar de nuevo en\(L = 0\) e incrementar la mano de obra en pequeños incrementos. La distancia vertical a la\(VMP\) línea se sumaría a los ingresos totales por cada incremento en la mano de obra. Sumar cada una de estas líneas verticales entre\(L= 0\) y\(L = LE\) arroja los ingresos totales obtenidos por la firma y viene dado por el área total sombreada.

Por último, dado que sólo hay dos factores de producción —el trabajo y el capital específico— se debe deducir que los ingresos totales equivalen a la suma de la factura salarial y la de capital, donde la factura de capital representa la cantidad total de dinero que se paga a los propietarios de capital. En forma de ecuación podríamos escribir

\[ total \: revenue = wage \: bill + capital \: bill \nonumber .\]

Dado que el ingreso total viene dado por el área sombreada total y la factura salarial viene dada por el área sombreada inferior, la factura capital debe estar dada por el área sombreada púrpura superior. Nuevamente, esta área representa la cantidad total de dinero que la firma debe pagar a los propietarios del capital utilizado en la producción. No es la tasa de alquiler, sin embargo. La tasa de renta viene dada por la factura de renta dividida por la cantidad total de unidades de capital utilizadas en la producción. Es decir, la tasa de renta en textiles,\(r_T\), viene dada por

\[ r_T = rental \: bill/K_T \nonumber ,\]

donde\(K_T\) está la cantidad fija de capital específico disponible para su uso en la industria.

De igual manera, la tasa salarial en textiles\(w_T\),, viene dada por

\[ w_T = wage \: bill/LE \nonumber .\]

Equilibrio de dos firmas en el modelo de factor específico

La economía se compone de dos industrias, la textil y la siderúrgica, cada una de las cuales está eligiendo insumos de mano de obra para maximizar las ganancias. Así, cuando ambas industrias operan y ambas maximizan las ganancias,

\[w_T = VMP_T \nonumber \]

para textiles y

\[ w_S = VMP_S \nonumber \]

para el acero, donde\(w_T\) y\(w_S\) son las tasas salariales que se pagan a los trabajadores en textiles y acero, respectivamente. Con una mano de obra homogénea y perfectamente móvil, también debe sostenerse otra condición, a saber, la restricción laboral:

\[ L_T + L_S = L \nonumber .\]

Es decir, la mano de obra utilizada en la producción textil (\(L_T\)) más la mano de obra utilizada en la producción de acero (\(L_S\)) debe ser igual a la dotación total de mano de obra disponible en la economía (\(L\)). Por último, debido a que el trabajo es homogéneo y perfectamente móvil entre industrias, los salarios deben ser igualados en equilibrio entre ambas industrias. Por lo tanto

\[w_T = w_S \nonumber .\]

Las cuatro condiciones deben cumplirse simultáneamente en un equilibrio en este modelo. Para representar este equilibrio y proporcionar un medio para analizar posibles cambios, presentamos un diagrama desarrollado por Mussa (1974). El diagrama (mostrado en la Figura\(\PageIndex{3}\)) es único ya que presenta las cuatro condiciones juntas en la misma gráfica. El eje horizontal del diagrama traza la oferta de mano de obra. El eje vertical traza el salario y el valor de los productos marginales.

Figura\(\PageIndex{3}\): Modelo de factor específico—Diagrama de Mussa

La longitud horizontal de la Figura\(\PageIndex{3}\),\(O_TO_S\), representa la dotación de mano de obra (\(L\)), la cantidad total de mano de obra disponible para su uso en la economía. La\(VMP_T\) línea desciende desde la izquierda como se presentó antes. No obstante, la\(VMP_S\) línea desciende desde la derecha. Esto se debe a que el punto\(O_S\) corresponde a cero unidades de mano de obra utilizadas en la producción de acero y\(O_TO_S\) unidades de mano de obra utilizadas en textiles. A medida que avanzamos hacia la izquierda\(O_S\), la mano de obra utilizada en el acero aumenta, mientras que la mano de obra utilizada en textiles disminuye. Así la\(VMP_S\) línea es volteada y dibujada con respecto a su origen en\(O_S\). Cada punto a lo largo del eje horizontal corresponde a una asignación de mano de obra entre las dos industrias que satisfacen la condición de restricción laboral. Así, en un punto como\(A\),\(O_TA\) las unidades de trabajo se utilizan en la producción textil (\(L_T\)) y\(O_SA\) las unidades de mano de obra se utilizan en la producción de acero (\(L_S\)). La suma de los dos iguales\(O_TO_S\), que es la dotación laboral total (\(L\)).

En el punto\(E\) de la Figura\(\PageIndex{3}\), las dos\(VMP\) líneas se cruzan de manera que\(VMP_T = VMP_S\), determinando la tasa salarial única\( w = w_T = w_S \) utilizando toda la mano de obra disponible,\(O_TO_S\). Por lo tanto, en el punto\(E\) se cumplen las cuatro condiciones de equilibrio enumeradas.

Efectos de un incremento de precio

Los precios cambiarán siempre que un país pase de la autarquía al libre comercio o cuando un país impone una política comercial o interna. En esta etapa, simplemente consideraremos los efectos de un cambio de precio dentro del contexto del modelo sin especificar por qué ocurrió el cambio. (En términos más técnicos, decimos que el cambio de precio es exógeno.) Posteriormente, presentaremos varias situaciones para ver cómo las políticas comerciales o comerciales afectarán los resultados en el modelo de factor específico (SF).

Supongamos que comenzamos con un país que produce textiles y acero en un equilibrio inicial dado por punto\(E\) en la Figura\(\PageIndex{4}\). El valor original de las líneas marginales de productos viene dado por\(VMP_{T1}\) y\(VMP_{S1}\), respectivamente. La asignación inicial de mano de obra es\(O_TA\) unidades a textiles y\(O_SA\) unidades a acero. La tasa salarial inicial en ambas industrias es\(w_1\).

Figura\(\PageIndex{4}\): Efectos de un incremento de precio

Ahora supongamos que el precio del acero aumenta exógenamente. El efecto inmediato será elevar el valor del producto marginal del acero, desplazándose\(VMP_{S1}\) hasta\(VMP_{S2}\). El nuevo equilibrio se da en el punto\(F\). En\(F\), la mano de obra destinada a la producción de acero habrá subido a\(O_SB\), mientras que la mano de obra utilizada en textiles habrá caído a\(O_TB\). El salario de equilibrio aumenta a\(w_2\).

La intuición para estos cambios se deriva de los efectos dinámicos subyacentes. Al principio, cuando sube el precio del acero, las tasas salariales y de alquiler permanecen fijas. Esto significa que los ingresos del acero aumentan mientras los costos siguen siendo los mismos, estimulando un aumento en las ganancias del acero. El beneficio positivo, en un mercado perfectamente competitivo, induce nuevas entradas de firmas a la producción de acero, expansión de firmas actuales en la industria, o ambas. Para expandirse, el acero debe inducir a los trabajadores a pasar de la producción textil. Esto requiere un incremento en el salario ya que la demanda laboral excede temporalmente la oferta laboral. Para evitar que toda la mano de obra se traslade al acero, la industria textil también debe elevar el salario a sus trabajadores. A medida que la mano de obra pasa de los textiles al acero y a medida que aumenta el salario, aumentan los costos de producción en acero y textiles. En el acero, esto erosiona las ganancias temporales que estaba obteniendo. Los textiles responden a los mayores costos recortando la producción y liberando a los trabajadores. Recuerde, no hay capacidad para expandir los insumos de capital en el acero ya que asumimos que el capital social del acero está fijo exógenamente en tamaño, y debido a la especificidad, el capital no se puede mover de la industria textil. Al final, las ganancias de la industria son impulsadas a cero en ambas industrias una vez que el salario sube suficientemente.

Nuestra principal preocupación, sin embargo, es el efecto del aumento de precios en los pagos o devoluciones de los factores. Es decir, ¿cómo se ven afectados los salarios y las tasas de renta del capital por el incremento del precio del acero? Ya se muestra la respuesta para los salarios. Podemos ver que los salarios suben para los trabajadores de ambas industrias. Sin embargo, nos importa no solo cómo cambia el salario nominal (dinero) sino, lo que es más importante, cómo cambia el salario real. Es decir, necesitamos identificar cómo cambia el poder adquisitivo de los salarios cuando aumenta el precio del acero. También queremos saber cómo cambian las tarifas reales de renta.

Efecto Salarial Real

Cuando el precio del acero sube de\(P_{S1}\) a\(P_{S2}\), el valor de la línea marginal de productos se desplaza proporcionalmente al incremento del precio. Esto se debe a que el precio del acero entra multiplicativamente en el valor de la fórmula del producto marginal, es decir,\(VMP_S = P_SMP_S\). El cambio porcentual en el precio del acero\( \hat P_S\) se deriva en la Figura\(\PageIndex{4}\) como

\[ \hat P_S = \frac{DA − EA}{EA} = \frac{DE}{EA} \nonumber .\]

He aquí por qué. Primero, la distancia\(DA\) es el valor del producto marginal para el uso de mano de obra\(O_SA\) cuando el precio del acero es\(P_{S2}\). La distancia\(EA\) es el valor del producto marginal para el uso de mano de obra\(O_SA\) cuando el precio del acero es\(P_{S1}\). Por lo tanto

\[ \frac{DA−EA}{EA} = \frac{ P_{S2}MP_S − P_{S1}MP_S}{P_{S1}MP_S} = \frac{P_{S2} − P_{S1}}{P_{S1}} = \hat P_S \nonumber .\]

Tenga en cuenta que\(MP_S\) cancela porque se evalúa al mismo insumo laboral dado por punto\(A\).

De igual manera, dado que\(FB\) es el salario de equilibrio al precio del acero\(P_{S2}\) y\(CB\) es el salario al precio del acero\(P_{S1}\), el cambio porcentual en el salario de equilibrio\(\hat w\) viene dado por

\[ \hat w = \frac{FB − CB}{CB} = \frac{FC}{CB} \nonumber .\]

De la Figura\(\PageIndex{4}\), es obvio que\( \hat P_S > \hat w \), lo que significa que el cambio porcentual en el precio del acero supera el cambio porcentual en la tasa salarial.

Dado que en el ejercicio el precio de los textiles se mantiene constante\( \hat P_T = 0 \),, podemos ampliar la desigualdad a

\[ \hat P_S > \hat w > \hat P_T \nonumber .\]

Ya que\( \hat P_S > \hat w \), esto implica que\(w/P_S\), el salario real en cuanto a compras de acero, disminuye. Es decir, los trabajadores de ambas industrias podrán comprar menos acero después del incremento del precio del acero que antes. No obstante\(\hat w > \hat P_T \), lo que implica que\(w/P_T\), el salario real en materia de compras textiles, aumenta. Esto significa que todos los trabajadores podrán comprar más textiles después del incremento del precio del acero que antes. En términos de bienestar general, los trabajadores perderán en total si tienden a comprar más productos siderúrgicos y menos productos textiles. Sin embargo, si las preferencias de una persona se inclinan hacia más textiles que el acero, entonces la persona puede estar mejor.

Efecto de Renta Real

Cuando el precio del acero sube de\(P_{S1}\) a\(P_{S2}\), la factura de renta en la industria siderúrgica sube de área\(KEI\)\(JFH\) en área en Figura\(\PageIndex{4}\). Dado que el monto de capital en acero permanece fijo, esto debe significar que la tasa de renta del capital siderúrgico aumente. No obstante, simplemente mirando el diagrama, es imposible saber si ese incremento excede o no alcanza el cambio porcentual en el precio del acero. Discutiremos más a fondo este tema.

La factura de renta en la industria textil cae de un área\(w_1EG\) a otra\(w_2FG\) en la Figura\(\PageIndex{4}\). Dado que el monto de capital en acero permanece fijo, esto debe significar que la tasa de renta del capital textil disminuya. Además, dado que el precio del acero aumenta y el precio de los textiles se mantiene igual, debe seguir eso\(r_T/P_S\) y\(r_T/P_T\) disminuir. Por lo tanto, la tasa real de renta sobre el capital textil debe caer con respecto a las compras de ambos bienes cuando el precio del acero aumente.

Efecto de aumento

Jones (1971) derivó matemáticamente un ordenamiento definitivo de los cambios porcentuales en todos los bienes y precios factoriales en un modelo SF de dos buenos. Véase R. W. Jones, “Un modelo de tres factores en teoría, comercio e historia”, en Comercio, balanza de pagos y crecimiento, ed. J. N. Bhagwati, R. W. Jones, R. A. Mundell, y J. Vanek (Ámsterdam: Nort-Holland Publishing Co., 1971). El efecto de aumento para el modelo SF es análogo al efecto de aumento para los precios demostrado en el modelo Heckscher-Ohlin (H-O). Define un orden de cambios porcentuales en los precios de los factores inducidos por cambios en los precios de las mercancías. Así supongamos que el precio del acero sube en un porcentaje mayor que el precio de los textiles tal que PS>PT. Esto puede ocurrir si dos países se mueven juntos en el comercio o si se cambia una política comercial o interna. Jones demostró que el efecto de aumento en este caso sería

\[ \hat r_S > \hat P_S > \hat w > \hat P_T > \hat r_T \nonumber .\]

Desde\( \hat r_S > \hat P_S \) y\( \hat r_S > \hat P_T \), esto implica\(r_S/P_S\) y\(r_S/P_T\) ambos aumentan. De esta manera, los rendimientos reales al capital siderúrgico aumentan con respecto a ambos bienes.

Desde\( \hat P_S > \hat r_T \) y\(\hat P_T > \hat r_T \),\(r_T/P_S\) y\(r_T/P_T\) ambos disminuyen. De esta manera, los rendimientos reales al capital textil disminuyen con respecto a ambos bienes. Por último, ya que\(\hat P_S > \hat w \)\(w/P_S\),, el salario real en cuanto a compras de acero, disminuye. Así los trabajadores podrán comprar menos acero que antes. No obstante\( \hat w > \hat P_T \), lo que implica que\(w/P_T\), el salario real en materia de compras textiles, aumenta. Esto significa que todos los trabajadores podrán comprar más textiles que antes.

Se puede escribir una versión alternativa del efecto de aumento en este modelo para el caso en que el precio de los textiles suba en un porcentaje mayor que el precio del acero tal que\( \hat P_T > \hat P_S \). El efecto de aumento en este caso se convierte

\[ \hat r_T > \hat P_T > \hat w > \hat P_S > \hat r_S \nonumber .\]

Esto implica que los rendimientos reales al capital en la industria textil aumentan, y los rendimientos reales al capital en la industria siderúrgica disminuyen con respecto a las compras de ambos bienes. Como antes, sin embargo, el efecto sobre los salarios es mixto. Los salarios reales con respecto a las compras de acero aumentan, mientras que los salarios reales con respecto a las compras textiles caen.

Efectos del comercio

Dado que este modelo es una variación del modelo H-O, se asume que las tecnologías de producción son idénticas entre países y el comercio ocurre debido a diferencias en las proporciones de los factores. Dado que existen ostensiblemente tres factores —el trabajo, el capital textil y el capital siderúrgico—, el país exportará aquellos bienes que utilicen su factor relativamente abundante de manera más intensa. Generalmente, este modelo se analiza asumiendo que un país se ajusta al patrón comercial descrito por el modelo H-O.

Así, si la producción de acero es intensiva en capital y el país es abundante en capital, entonces en la autarquía el precio del acero será relativamente más bajo a nivel nacional que en el extranjero, mientras que el precio de los textiles será relativamente mayor. Al abrir el comercio, el precio del acero comenzará a subir a medida que se exporta el acero y el precio de los textiles caerá a medida que se importen los textiles. Estos cambios de precios son todo lo que uno necesita para aplicar el efecto de aumento.

Si asumimos que el comercio conduce a\( \hat P_S > \hat P_T \), entonces\( \hat r_S > \hat P_S > \hat w > \hat P_T > \hat r_T \). Esto implica que el retorno al capital en la industria exportadora (acero) sube, mientras que el retorno al capital en la industria competidora de importaciones (textiles) cae. El retorno a la mano de obra móvil aumenta con respecto a los bienes importados pero cae con respecto a los bienes de exportación.

En contraste, si un país experimenta el cambio de precio opuesto tal que\( \hat P_T > \hat P_S \), entonces el país debe estar exportando textiles e importando acero. Esto implica\( \hat r_T > \hat P_T > \hat w > \hat P_S > \hat r_S \). Así el retorno al capital en la industria exportadora (textiles) aumenta, mientras que el retorno al capital en la industria competidora de importaciones (acero) disminuye. El retorno a la mano de obra móvil aumenta con respecto a los bienes importados pero cae con respecto a los bienes de exportación.

Ahora podemos afirmar de manera más formal y general que si el capital es inmóvil entre industrias (o específico de una industria) y si el trabajo es homogéneo y libremente móvil entre industrias, entonces el libre comercio provocará un incremento en los alquileres reales obtenidos por el capital en la industria exportadora, una disminución en los alquileres reales ganados por el capital de la industria competidora de importaciones, un incremento en los salarios reales respecto a las compras de los bienes de importación y una disminución de los salarios reales respecto a las compras de los bienes de exportación.

Claves para llevar

• El modelo de factor específico (SF) es una variante del modelo H-O que asume que el capital es específico de una industria, mientras que la mano de obra es libremente móvil entre industrias.
• El diagrama de Mussa muestra cómo el incremento en el precio de un producto eleva los salarios, eleva la tasa de renta sobre el capital específico de esa industria y baja la renta sobre capital específico de la otra industria.
• El efecto de aumento en el modelo SF demuestra que la renta real sube en la industria exportadora y cae en la industria importadora.
• El efecto de aumento en el modelo SF demuestra que los salarios reales en ambas industrias suben con respecto a las compras del bien de importación y caen con respecto a las compras del bien de exportación.

Ejercicio\(\PageIndex{1}\)

1. Preguntas de Jeopardy. Al igual que en el popular programa de juegos de televisión, se te da una respuesta a una pregunta y debes responder con la pregunta. Por ejemplo, si la respuesta es “un impuesto a las importaciones”, entonces la pregunta correcta es “¿Qué es un arancel?”
   1. El término utilizado para describir la cantidad de dólares adicionales obtenidos de una unidad adicional de insumo de mano de obra aplicada en la producción.
   2. El valor del producto marginal se encuentra multiplicando el producto marginal por esta variable.
   3. Una condición que se satisface en el modelo factorial específico en el nivel de producción maximizador de ganancias.
   4. El término que describe la suma de la factura salarial total y la factura de capital total.
   5. De aumentar, disminuir, o permanecer igual, el efecto sobre el valor del producto marginal de la uva cuando hay una disminución en el precio de mercado de la uva en un modelo factorial específico.
   6. De aumentar, disminuir, o permanecer igual, el efecto sobre la factura salarial en la industria de la uva cuando hay un incremento en el precio de mercado de la uva en un modelo factorial específico.
   7. De aumentar, disminuir, o permanecer igual, el efecto sobre la tasa salarial de equilibrio cuando hay una disminución en el precio de mercado de uno de dos bienes en un modelo factorial específico.
   8. El efecto de aumento para los precios en un modelo de dos buenos factores específicos con capital específico y mano de obra móvil cuando un país se abre al comercio y exporta leche e importa galletas.
   9. El efecto de aumento para los precios en un modelo de dos buenos factores específicos con capital específico y mano de obra móvil cuando un país que exporta vino e importa queso pasa del libre comercio a la autarquía.