Si queremos que la gente trabaje más, ¿deberíamos pagarles más o eso hará que trabajen menos?
Considere a un taxista que sea dueño de un automóvil, el dueño de una tienda de conveniencia o cualquier otra persona que pueda establecer su propio horario. El trabajo tiene dos efectos en este consumidor: más consumo de bienes pero menos consumo de ocio. Para modelar esto, dejamos x ser el consumo de bienes, L la cantidad de tiempo no laboral o de ocio, y el tiempo de trabajo T — L, donde T es la cantidad de tiempo disponible para actividades de todo tipo. La variable L incluye muchas actividades que no necesariamente son divertidas, como viajes al dentista, cortes de pelo y dormir, pero por las que no se paga al consumidor y que representan opciones. Se podría argumentar que dormir no es realmente una opción, en el sentido de que no se puede elegir dormir cero; pero esto se puede manejar ajustando T para representar “tiempo disponible para el comportamiento elegido” de modo que T — L sea tiempo de trabajo y L se elija actividades no laborales. Ponemos a L como ocio en lugar de oferta de mano de obra porque lo bueno es el ocio, mientras que la mayoría de nosotros vemos el trabajo como algo que estamos dispuestos a hacer siempre que nos paguen por ello.
La oferta laboral es diferente de otros consumos porque el salario entra en la restricción presupuestal dos veces: primero como precio del ocio, y segundo como ingreso del trabajo. Una forma de expresar esto es escribir la restricción presupuestal del consumidor como\(\begin{equation}p x+w L=M+w T\end{equation}\).
Aquí, M representa ingresos no laborales, como obsequios, transferencias gubernamentales e ingresos por intereses. Bajamos el subíndice sobre el precio de X y usamos w como salario. Por último, usamos una L mayúscula para el ocio porque una L minúscula se parece al número uno. La idea un tanto dickensiana es que el presupuesto máximo del consumidor implica trabajar el total de horas disponibles T, y las horas no trabajadas se compran a la tasa salarial w. Alternativamente, se podría expresar la restricción presupuestal para reflejar que los gastos en bienes px equivalen al dinero total, que es la suma de ingresos no laborales M e ingresos laborales\(\begin{equation}w(T-L), \text { or } p x=M+w(T-L)\end{equation}\).
Estas dos formulaciones de la restricción presupuestal son matemáticamente equivalentes.
La estrategia para resolver el problema también es equivalente a la formulación estándar, aunque existe cierta claridad expositiva utilizada al emplear la restricción presupuestal para eliminar x, es decir, escribimos la utilidad\(\begin{equation}u(x, L) \text { as } h(L)=u(M+w(T-L) p L)\end{equation}\).
Como antes, obtenemos la condición de primer orden\(\begin{equation}0=h^{\prime}\left(L^{*}\right)=-u 1(w p)+u 2\end{equation}\), donde se evalúan las derivadas parciales u 1 y u 2 en\(\begin{equation}\left(M+w\left(T-L^{*}\right) p, L^{*}\right)\end{equation}\). Tenga en cuenta que la condición de primer orden es la misma que la teoría estándar de dos buenos desarrollada ya. Esto se debe a que el efecto, hasta el momento, es meramente requerir dos componentes para el ingreso: M y wT, ambos de los cuales son constantes. Es sólo cuando evaluamos el efecto de un incremento salarial que vemos una diferencia.
Para evaluar el efecto de un incremento salarial, diferenciar la condición de primer orden para obtener
\ begin {ecuación} 0= (u 11 (w p) 2-2 u 12 (w p) +u 22) d L d w-u 1 p- (w p) u 11 T-L p+u 12 T-L p\ end {ecuación}
Desde\(\begin{equation}\text { u } 11(\text { w } p) 2-2 \text { u } 12(w p)+u 22<0\end{equation}\)
por la condición estándar de segundo orden,
dL dw >0 si y solo si u 1 p + (w p) u 11 T−L p − u 12 T−L p <0;
es decir, estas expresiones son equivalentes entre sí. Simplificando esto último, obtenemos − (w p) u 11 T−L p + u 12 T−L p u 1 p >1, o (T−L) − (w p) u 11 + u 12 u 1 >1, o L Log (u 1) > 1 T−L =− L Log (T−L), o L Log (u 1) + LL Log (T−L) + L Log (T−L) + L Log (u 1) + LL Log (−L) >0, o L Log (u 1 (T−L)) >0.
Dado que el logaritmo va en aumento, esto equivale a que u 1 (T−L) sea una función creciente de L. Es decir, L sube con un incremento en los salarios y una disminución en las horas trabajadas si la utilidad marginal de los bienes multiplicada por las horas trabajadas es una función creciente de L, manteniendo constante todo lo demás, pero evaluada a los valores óptimos. El valor u 1 es el valor marginal de un bien adicional, mientras que el valor T — L representa las horas trabajadas. Así, en particular, si los bienes y el ocio son sustitutos, de manera que un incremento en L disminuye el valor marginal de los bienes, entonces un incremento en los salarios debe disminuir el ocio, y la oferta laboral aumenta en los salarios. El caso donde los bienes son complementos tiene la esperanza de una oferta de mano de obra decreciente, por lo que consideramos primero el caso extremo de los complementos.
En este caso, el consumidor hará que el consumo y el ocio sean iguales para maximizar la utilidad, entonces\(\begin{equation}\mathrm{M}+\mathrm{w}\left(\mathrm{T}-\mathrm{L}^{*}\right) \mathrm{p}=\mathrm{L}^{*} \text { or } \mathrm{L}^{*}=\mathrm{M}+\mathrm{wT} \mathrm{p} 1+\mathrm{w} \mathrm{p}=\mathrm{M}+\mathrm{wT} \mathrm{p}+\mathrm{w}\end{equation}\).
Así, L está aumentando en los salarios si pT > M; es decir, si M es lo suficientemente pequeño para que uno no pueda comprar todas las necesidades de uno y no trabajar en absoluto. (Este es el único caso razonable para esta función de utilidad). Con fuertes complementos entre bienes y ocio, un incremento en los salarios induce menos horas trabajadas.
Ejemplo (Cobb-Douglas):\(\begin{equation}h(L)=(M+w(T-L) p) a L 1-a\end{equation}\).
La condición de primer orden da\(\begin{equation}0=h^{\prime}(L)=-a(M+w(T-L) p) a-1\lfloor 1-a w p+(1-a)(M+w(T-L) p) a L-a\end{equation}\)
o\(\begin{equation}\text { al } w p=(1-a) M+w(T-L) p\end{equation}\),
Si M es lo suficientemente alto, el consumidor no trabaja sino que toma L = T; de lo contrario, la ecuación da el ocio, y la oferta de trabajo viene dada por T−L=Max {0, αT− (1−α) (M w)}.
La oferta laboral aumenta con el salario, por alto que vaya el salario.
El salario afecta no sólo el precio del ocio sino también el nivel de ingresos. Esto hace posible que el efecto ingreso de un incremento salarial domine el efecto de sustitución. Además, vimos que esto es más probable cuando el consumo de bienes lleva tiempo; es decir, los bienes y el ocio son complementos.
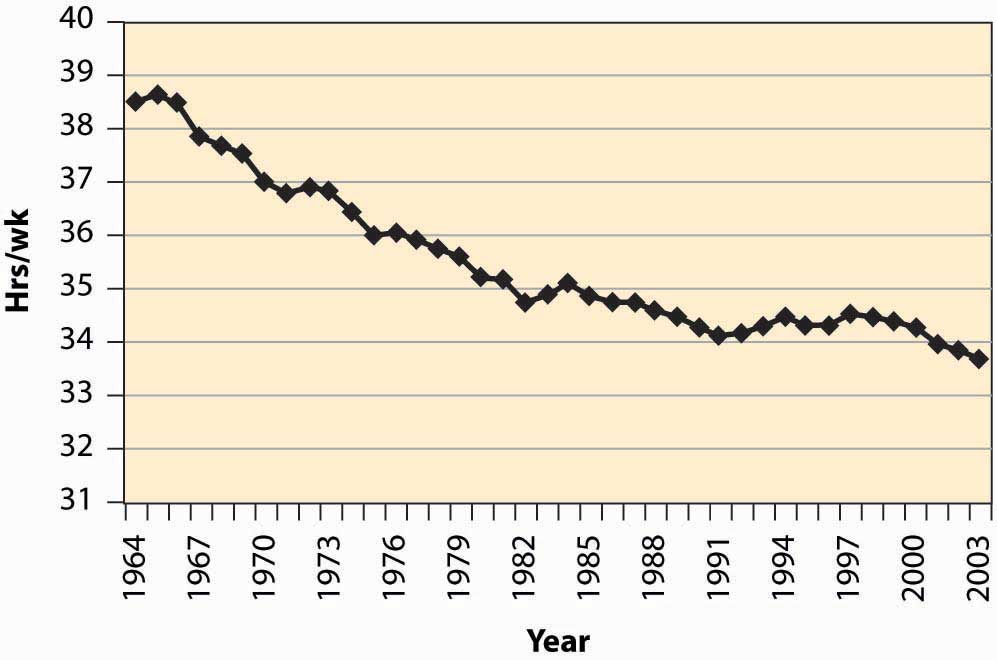
Figura 13.1 Horas por semana
Figura 13.1 “Horas por semana” ilustra.
Varios físicos han cambiado de carrera para convertirse en investigadores en finanzas o economía financiera. La investigación en finanzas paga sustancialmente mejor que la investigación en física y, sin embargo, requiere muchas de las mismas habilidades matemáticas como el cálculo estocástico. Los físicos que ven a sus ex colegas manejando Porsches y comprando casas de verano están comprensiblemente molestos porque la investigación en finanzas —que intelectualmente no es más difícil ni desafiante que la física— paga mucho mejor. En efecto, algunos físicos están diciendo que otros campos —como las finanzas, la economía y el derecho— “no deberían” pagar más que la física.
La diferencia de ingresos entre los investigadores de la física y los investigadores de finanzas es un ejemplo de un diferencial compensador. Un diferencial compensador son los ingresos o costos que igualan diferentes opciones. Hay individuos que podrían convertirse en físicos o investigadores financieros. A igualdad de ingresos, demasiados eligen la física y muy pocos eligen las finanzas, en el sentido de que hay un excedente de físicos y escasez de investigadores de finanzas. Los salarios de las finanzas deben superar los salarios de la física para inducir a algunos de los investigadores que son capaces de hacer cualquiera de las dos a cambiar a las finanzas, lo que compensa a esos individuos por hacer la tarea menos deseable.
Los trabajos que sean peligrosos o desagradables deben pagar más que los trabajos que requieran habilidades similares pero sin los malos atributos. De esta manera, los trabajadores de yacimientos petrolíferos en la Pendiente Norte de Alaska, muy por encima del Círculo Polar Ártico, ganan una prima sobre los trabajadores en trabajos similares en Houston La prima —o salario diferencial— debe ser tal que el trabajador marginal sea indiferente entre las dos opciones: El salario extra compensa al trabajador por las condiciones de trabajo adversas. Es por ello que se conoce en la jerga económica por la frase de un diferencial compensador.
Los altos salarios que ganan los basquetbolistas profesionales no están compensando diferenciales. Estos salarios no se crean por la necesidad de inducir a las personas altas a elegir el basquetbol sobre trabajos alternativos como pintar techos, sino que son pagos que reflejan la rareza de las habilidades y habilidades involucradas. Los diferenciales compensadores están determinados por alternativas, no por la escasez directa. Los basquetbolistas profesionales están bien pagados por la misma razón que los cuadros de Picasso son caros: No hay muchos de ellos relativos a la demanda.
Un diferencial compensador es una característica de otras opciones, así como de las elecciones de carrera. Por ejemplo, a muchas personas les gustaría vivir en California por su clima y belleza escénica. Dada la conveniencia de California sobre, por ejemplo, Lincoln, Nebraska, o Rochester, Nueva York, debe haber un diferencial compensador para vivir en Rochester; y dos significativos son la calidad del aire y los precios de la vivienda. La calidad del aire empeora a medida que aumentan las poblaciones, tendiendo así a crear un diferencial compensador. Además, el incremento en los precios de la vivienda también tiende a compensar —la vivienda es barata en Rochester, al menos en comparación con California.Hay otras compensaciones, además de la vivienda, por vivir en Rochester—esquí de fondo y proximidad a montañas y lagos, por ejemplo. Generalmente, el empleo es sólo un factor temporal que podría compensar, porque el empleo tiende a ser móvil, también, y trasladarse a la ubicación que prefieran los trabajadores, cuando sea posible. No es posible en la vertiente norte de Alaska.
Los precios de la vivienda también compensan la ubicación dentro de una ciudad. Para la mayoría de las personas, es más conveniente, tanto en el tiempo de viaje como para los servicios, estar ubicado cerca del distrito central de negocios que en los suburbios periféricos. Los principales diferenciales compensatorios son la calidad escolar, los índices de criminalidad y los precios de la vivienda. Ilustramos las ideas con un modelo sencillo de ciudad en la siguiente sección.
Claves para llevar
El tiempo libre, el tiempo que se pasa sin trabajar, es bueno como otros bienes, y el costo de los servicios públicos de trabajar es menos ocio.
La oferta laboral es diferente de otros bienes porque el salario entra dos veces en la restricción presupuestal, primero como precio del ocio y segundo como ingreso del trabajo.
Si los bienes y el ocio son sustitutos, de manera que un incremento en L disminuye el valor marginal de los bienes, entonces un aumento en los salarios debe disminuir el ocio, y la oferta laboral aumenta en los salarios.
Con fuertes complementos entre bienes y ocio, un incremento en los salarios induce menos horas trabajadas.
La complementariedad entre bienes y ocio es razonable porque lleva tiempo consumir bienes.
Para la mayoría de las naciones desarrolladas, los aumentos en los salarios están asociados con menos horas trabajadas.
Un diferencial compensador son los ingresos o costos que igualan diferentes opciones.
Los trabajos que sean peligrosos o desagradables deben pagar más que los trabajos que requieran habilidades similares pero sin los malos atributos.
La prima —o salario diferencial— debe ser tal que el trabajador marginal sea indiferente entre las dos opciones: El salario extra compensa al trabajador por las condiciones de trabajo adversas.
La elección de la ciudad también está sujeta a diferenciales compensatorios, y los diferenciales significativos incluyen calidad del aire, tasas de criminalidad, tasas impositivas y precios de vivienda.
EJERCICIOS
Una pregunta de pensamiento: ¿Un legado motivo—el deseo de dar dinero a los demás— cambia la probabilidad de que los bienes y el ocio sean complementos?
Mostrar que un incremento en el salario incrementa el consumo de bienes; es decir, x aumenta cuando aumenta el salario.
