Hay muchos riesgos en la vida, incluso si uno no se suma a estos riesgos comprando intencionalmente boletos de lotería. Los precios de la gasolina suben y bajan, la demanda de personas capacitadas en tu especialidad fluctúa y los precios de las casas cambian. ¿Cómo valora la gente los juegos de azar? El punto de partida para la investigación es el von Neumann-MorgensternJohn von Neumann (1903—1957) y Oskar Morgenstern (1902-1977) son los autores de Teoría de los Juegos y Comportamiento Económico (Princeton, NJ: Princeton University Press, 1944). función de utilidad. La idea de una función de utilidad von Neumann-Morgenstern para una persona determinada es que, para cada posible resultado x, hay un valor v (x) asignado por la persona, y el valor promedio de v es el valor que la persona asigna al resultado riesgoso. En otras palabras, la función de utilidad von Neumann-Morgenstern se construye de tal manera que un consumidor valora las apuesta como si fueran la utilidad esperada
Se trata de un enfoque de “estado del mundo”, en el sentido de que cada uno de los resultados está asociado a un estado del mundo, y la persona maximiza el valor esperado de los diversos estados posibles del mundo. Valor aquí no significa un valor monetario, sino un valor psíquico o utilidad.
Para ilustrar el supuesto, considere probabilidades iguales de ganar $100 y ganar $200. El resultado esperado de esta apuesta es de 150 dólares, el promedio de $100 y $200. No obstante, el valor real del resultado podría ser cualquier cosa entre el valor de $100 y el valor de $200. La utilidad von Neumann-Morgenstern es\(\begin{equation}1 / 2 v(\$ 100)+1 / 2 v(\$ 200)\end{equation}\)
La formulación de von Neumann-Morgenstern tiene ciertas ventajas, entre ellas la lógica de que lo que importa es el valor promedio del resultado. Por otro lado, en muchas pruebas, las personas se comportan de formas no consistentes con la teoría.Por ejemplo, las personas tienden a reaccionar con más fuerza ante eventos muy improbables de lo que es consistente con la teoría. Sin embargo, el enfoque de von Neumann es el modelo predominante de comportamiento bajo riesgo.
Para introducir la teoría, consideraremos solo los resultados monetarios, y sobre todo el caso de dos resultados monetarios. La persona tiene una función de utilidad von Neumann-Morgenstern v de estos resultados. Si los posibles resultados son x 1, x 2,..., x n y estos ocurren con probabilidad π 1, π 2,..., π n respectivamente, la utilidad del consumidor es
\ begin {ecuación} u= π 1 v (x 1) + π 2 v (x 2) +... + π n v (x n) = i=1 n π i v (x i). \ end {ecuación}
Este es el significado de “tener una función de utilidad von Neumann-Morgenstern” —esa utilidad se puede escribir en esta forma de suma ponderada.
La primera visión que fluye de esta definición es que a un individuo no le gusta el riesgo si v es cóncavo. Para ver esto, tenga en cuenta que la definición de concavidad postula que v es cóncava si, para todos π en [0, 1] y todos los valores x 1 y x 2,\(\begin{equation}v(n \times 1+(1-n) \times 2) \geq \pi v(\times 1)+(1-n) v(\times 2)\end{equation}\)
Para funciones suavemente diferenciables, la concavidad equivale a una segunda derivada que no es positiva. Mediante la inducción, la definición de concavidad puede generalizarse para mostrar\(\begin{equation}v( π 1 x 1 + π 2 x 2 +…+ π n x n )≥ π 1 v( x 1 )+ π 2 v( x 2 )+…+ π n v( x n ).\end{equation}\).
Figura 13.8 Equivalentes de utilidad esperada y certidumbre
Figura 13.8 “Equivalentes de utilidad esperada y certidumbre”. Hay dos posibles resultados: x 1 y x 2. El valor x 1 ocurre con probabilidad π, y x 2 con probabilidad 1 — π. Esto significa que el resultado promedio o esperado es\(\begin{equation}πx1 + (1 – π)x2\end{equation}\). El valor\(\begin{equation}v (πx1 + (1 – π)x2) \end{equation}\) es el valor en el resultado esperado\(\begin{equation}πx 1 + (1 – π)x2, while πv(x1) + (1 – π)v(x2)\end{equation}\) es el promedio del valor del resultado. Como es evidente en la figura, la concavidad hace que el resultado promedio sea preferible al resultado aleatorio. Las personas con funciones de utilidad cóncavas de von Neumann-Morgenstern son conocidas como personas con aversión al riesgo; prefieren el valor esperado de una apuesta a la apuesta misma.
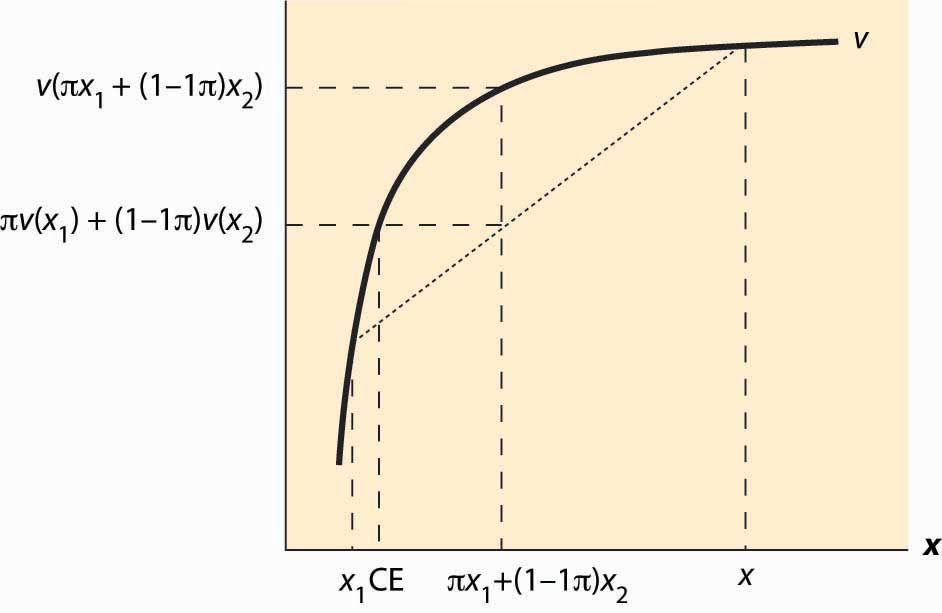
Un concepto útil es la certeza equivalente de una apuesta. El equivalente de certeza es una cantidad de dinero que proporciona igual utilidad al pago aleatorio de la apuesta. El equivalente de certeza se etiqueta CE en la figura. Tenga en cuenta que la CE es menor que el resultado esperado, si la persona es reacia al riesgo. Esto se debe a que las personas con aversión al riesgo prefieren el resultado esperado al resultado riesgoso.
La prima de riesgo se define como la diferencia entre el pago esperado (esto se expresa como πx1 + (1 — π) x2 en la figura) y el equivalente de certeza. Este es el costo del riesgo, es la cantidad de dinero que un individuo estaría dispuesto a pagar para evitar riesgos. Esto significa también que la prima de riesgo es el valor del seguro. ¿Cómo cambia la prima de riesgo de una apuesta determinada cuando se incrementa la riqueza base? Se puede demostrar que la prima de riesgo cae a medida que aumenta la riqueza para cualquier apuesta, si y sólo si\(\begin{equation}-v^{n}(x) v^{\prime}(x)\end{equation}\) va disminuyendo.
A la medida\(\begin{equation}\rho(x)=-v^{\prime \prime}(x) v^{\prime}(x)\end{equation} (x)\) se le conoce como la medida Arrow-Pratt de aversión al riesgo La medida recibió el nombre de sus descubridores, el premio Nobel Kenneth Arrow y John Pratt., y también como la medida de aversión absoluta al riesgo. Es una medida de aversión al riesgo calculada como la negativa de la relación de la segunda derivada de utilidad dividida por la primera derivada de utilidad. Para tener una idea de por qué es importante esta medida, considere una aproximación cuadrática a v. Sea μ el valor esperado, y deje que δ 2 sea el valor esperado de\ (\ begin {ecuación} (x-\ mu) ^ {2}\ end {ecuación}
). Entonces podemos aproximar v (CE) de dos maneras distintas.
Cancelando v (μ) de ambos lados y señalando que el valor promedio de x es μ, entonces E (x — μ) = 0, tenemos\(\begin{equation}\mathbf{v}^{\prime}(\mu)(\mathrm{CE}-\mu) \approx 1 / 2 \mathrm{v}^{\prime \prime}(\mu) \sigma 2\end{equation}\)
Es decir, la prima de riesgo —la diferencia entre el resultado promedio y el equivalente de certidumbre— es aproximadamente igual a la medida Flecha Pratt multiplicada por la mitad de la varianza, al menos cuando la varianza es pequeña.
La traducción del riesgo a dólares, a través de una prima de riesgo, se puede evaluar incluso para grandes juegos si estamos dispuestos a hacer algunas suposiciones técnicas. Si una empresa de servicios públicos tiene constante aversión absoluta al riesgo (CARA), la medida de aversión al riesgo no cambia con la riqueza; es decir, ρ=− v ″ (x) v ′ (x) es una constante. Esto resulta implicar, después de establecer la utilidad de cero a cero, eso\(\begin{equation}v(x)=1 \rho(1-e-\rho x)\end{equation}\). (Esta formulación se deriva estableciendo v (0) = 0, manejando el caso de ρ = 0 con los límites apropiados.) Ahora también supongamos que la apuesta x se distribuye normalmente con media μ y varianza δ 2. Entonces el valor esperado de v (x) es\(\begin{equation}\operatorname{Ev}(\mathrm{x})=1 \rho(1-\mathrm{e}-\rho(\mu-\rho 2 \sigma 2))\end{equation}\)
Es un resultado inmediato de esta fórmula que la certeza equivalente, con preferencias CARA y riesgos normales, es μ− ρ 2 σ 2. De ahí que la prima de riesgo de una distribución normal para un individuo CARA sea ρ 2 σ 2. Esta formulación aparecerá cuando consideremos la teoría de la agencia y los desafíos de motivar a un empleado reacio al riesgo cuando los resultados tengan un componente aleatorio sustancial.
Un aspecto importante de CARA con riesgos normalmente distribuidos es que las preferencias del consumidor son lineales en la media de la apuesta y la varianza. De hecho, dada una opción de apuesta, el consumidor selecciona la que tiene el mayor valor de μ− ρ 2 σ 2. Dichas preferencias suelen denominarse preferencias de varianza media, y describen a las personas que valoran el riesgo linealmente con el rendimiento esperado. Tales preferencias constituyen la base de la teoría financiera moderna.
Claves para llevar
La función de utilidad von Neumann-Morgenstern para una persona determinada es un valor v (x) para cada posible resultado x, y el valor promedio de v es el valor que la persona asigna al resultado riesgoso. Bajo esta teoría, las personas valoran el riesgo en la utilidad esperada del riesgo.
El enfoque de von Neumann es el modelo predominante de comportamiento bajo riesgo, aunque existen numerosas críticas a la teoría basadas en experimentos.
A un individuo no le gusta el riesgo si v es cóncava.
Para funciones suavemente diferenciables, la concavidad equivale a una segunda derivada que no es positiva.
Las personas con funciones de utilidad cóncavas de von Neumann-Morgenstern son conocidas como personas con aversión al riesgo.
El equivalente de certeza de una apuesta es una cantidad de dinero que proporciona igual utilidad a la recompensa aleatoria de la apuesta. El equivalente de certeza es menor al resultado esperado si la persona es reacia al riesgo.
La prima de riesgo se define como la diferencia entre el pago esperado y el equivalente de certeza.
La prima de riesgo cae a medida que aumenta la riqueza para cualquier apuesta, si y solo si − v ″ (x) v ′ (x) va disminuyendo.
La medida ρ (x) =− v ″ (x) v ′ (x) se conoce como la medida Flecha Pratt de aversión al riesgo, y también como la medida de aversión absoluta al riesgo.
La prima de riesgo es aproximadamente igual a la medida Flecha Pratt multiplicada por la mitad de la varianza cuando la varianza es pequeña.
La aversión absoluta al riesgo constante proporciona una base para las “preferencias de varianza media”, la base de la teoría financiera moderna.
EJERCICIOS
Utilice una aproximación cuadrática en ambos lados de la ecuación para agudizar la estimación de la prima de riesgo. Primero, tenga en cuenta que\(\begin{equation}v(μ)+ v ′ (μ)(CE−μ)+½ v ″ (μ) (CE−μ) 2 ≈v(CE) =E{v(x)}≈E{v(μ)+ v ′ (μ)(x−μ)+½ v ″ (μ) (x−μ) 2 }.\end{equation}\)
Concluir eso\(\begin{equation}\mu-\mathrm{CE} \approx 1 \rho(1+\rho 2 \sigma 2-1)\end{equation}\). Esta aproximación es exacta al segundo orden.
Supongamos que\(\begin{equation}u(x)=x^{0.95}\end{equation}\) para un consumidor con un nivel de riqueza de 50,000 dólares. Considera una apuesta, con igual probabilidad de ganar $100 y perder $100, y computar la prima de riesgo asociada con la apuesta.
Supongamos que\(\begin{equation}u(x)=x^{0.99}\end{equation}\) para un consumidor con un nivel de riqueza de 100.000 dólares. Un boleto de lotería cuesta $1 y paga $5,000,000 con la probabilidad 1 10,000,000. Calcular la certeza equivalente del boleto de lotería.
El rendimiento de las inversiones del Tesoro del Gobierno de Estados Unidos es de aproximadamente 3%. Así, una inversión de $1 devuelve $1.03 después de un año. Tratar esta rentabilidad como libre de riesgos. El mercado de valores (S&P 500) devuelve 7% en promedio y tiene una varianza que ronda el 16% (la varianza del rendimiento de una inversión de $1 es de 0.16 dólares). Calcular el valor de ρ para un individuo CARA. ¿Cuál es la prima de riesgo asociada a probabilidades iguales de una ganancia o pérdida de $100 dado el valor de ρ?
Un consumidor tiene utilidad\(\begin{equation}u(x)=x^{7 / 8}\end{equation}\) y una riqueza base de $100,000. Está a punto de participar en una apuesta que le dará 10.000 dólares (llevándola a 110.000 dólares) si un dado justo rueda menos de 3 (probabilidad 1/3), pero le costará $5,000 (dejándola con 95,000 dólares) de lo contrario.
¿Cuál es el equivalente de certeza de participar en esta apuesta?
¿Cuánto estaría dispuesta a pagar para evitar esta apuesta?
