13.3: Algunas pruebas básicas de hipótesis nulas
- Page ID
- 144615
En esta sección, observamos varios procedimientos comunes de prueba de hipótesis nulas. El énfasis aquí está en brindar suficiente información para permitirle realizar e interpretar las versiones más básicas. En la mayoría de los casos, las herramientas de análisis estadístico en línea mencionadas en el Capítulo 12 manejarán los cómputos, al igual que programas como Microsoft Excel y SPSS.
La prueba t
Como hemos visto a lo largo de este libro, muchos estudios en psicología se centran en la diferencia entre dos medios. La prueba de hipótesis nula más común para este tipo de relación estadística es la prueba t-. En esta sección, analizamos tres tipos de pruebas t que se utilizan para diseños de investigación ligeramente diferentes: la prueba t de una muestra, la prueba t- de muestras dependientes y la prueba t- de muestras independientes. Puede que ya hayas tomado un curso de estadística, pero vamos a actualizar tu estadística
Prueba t de una muestra
La prueba t de una muestra se utiliza para comparar una media muestral (M) con una hipotética media poblacional (μ 0) que proporciona algún estándar de comparación interesante. La hipótesis nula es que la media para la población (µ) es igual a la media hipotética de la población: μ = μ 0. La hipótesis alternativa es que la media para la población es diferente de la hipotética media poblacional: μ ≠ μ 0. Para decidir entre estas dos hipótesis, necesitamos encontrar la probabilidad de obtener la media muestral (o una extrema más) si la hipótesis nula fuera cierta. Pero encontrar este valor p requiere primero computar una estadística de prueba llamada t. (Un estadístico de prueba es un estadístico que se calcula solo para ayudar a encontrar el valor p.) La fórmula para t es la siguiente:
\[t=\frac{M-\mu_{0}}{\left(\dfrac{S D}{\sqrt{N}}\right)}\]
Nuevamente, M es la media de la muestra y µ 0 es la hipotética media poblacional de interés. SD es la desviación estándar de la muestra y N es el tamaño de la muestra.
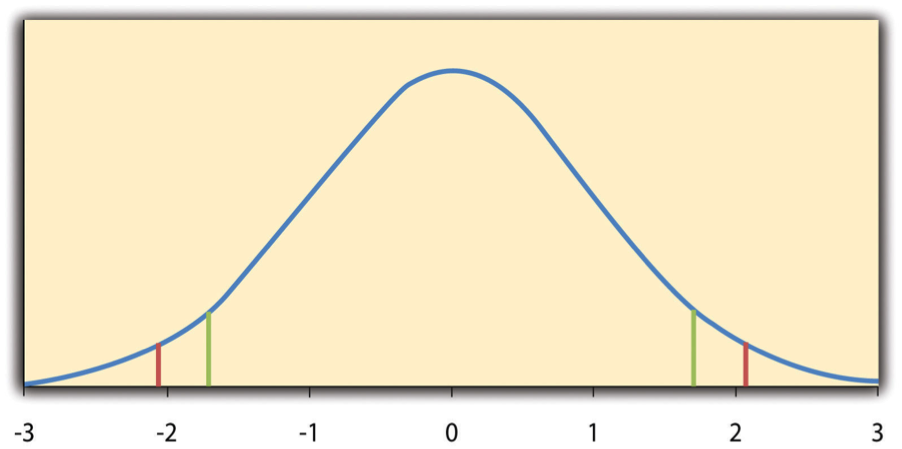
La razón por la que el estadístico t (o cualquier estadístico de prueba) es que sabemos cómo se distribuye cuando la hipótesis nula es verdadera. Como se muestra en la Figura\(\PageIndex{1}\), esta distribución es unimodal y simétrica, y tiene una media de 0. Su forma precisa depende de un concepto estadístico llamado grados de libertad, que para una prueba t de una muestra es N − 1. (Hay 24 grados de libertad para la distribución mostrada en la Figura\(\PageIndex{1}\).) El punto importante es que conocer esta distribución permite encontrar el valor p para cualquier puntuación t. Consideremos, por ejemplo, una puntuación t de 1.50 basada en una muestra de 25. La probabilidad de una puntuación t al menos este extremo viene dada por la proporción de t puntuaciones en la distribución que son al menos este extremo. Por ahora, definamos extremo como estar lejos de cero en cualquier dirección. Así, el valor p es la proporción de puntuaciones t que son 1.50 o superiores o que son −1.50 o inferiores —un valor que resulta ser .14.
Afortunadamente, no tenemos que ocuparnos directamente de la distribución de t scores. Si ingresáramos nuestros datos de muestra y la media hipotética de interés en una de las herramientas estadísticas en línea del Capítulo 12 o en un programa como SPSS (Excel no tiene una función de prueba t- de una muestra), el resultado incluiría tanto la puntuación t como el valor p. En este punto, el resto del procedimiento es sencillo. Si p es igual o menor que .05, rechazamos la hipótesis nula y concluimos que la media poblacional difiere de la media hipotética de interés. Si p es mayor a .05, conservamos la hipótesis nula y concluimos que no hay evidencia suficiente para decir que la media poblacional difiera de la hipotética media de interés. (Nuevamente, técnicamente, concluimos únicamente que no tenemos pruebas suficientes para concluir que sí difiere).
Si tuviéramos que calcular la puntuación t a mano, podríamos usar una tabla como Tabla\(\PageIndex{1}\) para tomar la decisión. Esta tabla no proporciona valores reales de p. En cambio, proporciona los valores críticos de t para diferentes grados de libertad (df) cuando α es .05. Por ahora, centrémonos en los valores críticos de dos colas en la última columna de la tabla. Cada uno de estos valores debe interpretarse como un par de valores: uno positivo y otro negativo. Por ejemplo, los valores críticos de dos colas cuando hay 24 grados de libertad son 2.064 y −2.064. Estos están representados por las líneas verticales rojas en la Figura\(\PageIndex{1}\). La idea es que cualquier puntuación t por debajo del valor crítico inferior (la línea roja izquierda en la Figura\(\PageIndex{1}\)) está en el 2.5% más bajo de la distribución, mientras que cualquier puntuación t por encima del valor crítico superior (la línea roja derecha) está en el 2.5% más alto de la distribución. Por lo tanto, cualquier puntuación t más allá del valor crítico en cualquier dirección está en el 5% más extremo de las puntuaciones t cuando la hipótesis nula es verdadera y tiene un valor p menor que .05. Así, si la puntuación t que calculamos está más allá del valor crítico en cualquier dirección, entonces rechazamos la hipótesis nula. Si la puntuación t que calculamos está entre los valores críticos superior e inferior, entonces conservamos la hipótesis nula.
| Valor crítico | ||
|---|---|---|
| df | De una cola | Dos colas |
| 3 | 2.353 | 3.182 |
| 4 | 2.132 | 2.776 |
| 5 | 2.015 | 2.571 |
| 6 | 1.943 | 2.447 |
| 7 | 1.895 | 2.365 |
| 8 | 1.860 | 2.306 |
| 9 | 1.833 | 2.262 |
| 10 | 1.812 | 2.228 |
| 11 | 1.796 | 2.201 |
| 12 | 1.782 | 2.179 |
| 13 | 1.771 | 2.160 |
| 14 | 1.761 | 2.145 |
| 15 | 1.753 | 2.131 |
| 16 | 1.746 | 2.120 |
| 17 | 1.740 | 2.110 |
| 18 | 1.734 | 2.101 |
| 19 | 1.729 | 2.093 |
| 20 | 1.725 | 2.086 |
| 21 | 1.721 | 2.080 |
| 22 | 1.717 | 2.074 |
| 23 | 1.714 | 2.069 |
| 24 | 1.711 | 2.064 |
| 25 | 1.708 | 2.060 |
| 30 | 1.697 | 2.042 |
| 35 | 1.690 | 2.030 |
| 40 | 1.684 | 2.021 |
| 45 | 1.679 | 2.014 |
| 50 | 1.676 | 2.009 |
| 60 | 1.671 | 2.000 |
| 70 | 1.667 | 1.994 |
| 80 | 1.664 | 1.990 |
| 90 | 1.662 | 1.987 |
| 100 | 1.660 | 1.984 |
Hasta el momento, hemos considerado lo que se denomina prueba de dos colas, donde rechazamos la hipótesis nula si la puntuación t para la muestra es extrema en cualquier dirección. Esta prueba tiene sentido cuando creemos que la media de la muestra podría diferir de la hipotética media poblacional pero no tenemos buenas razones para esperar que la diferencia vaya en una dirección particular. Pero también es posible hacer una prueba de una cola, donde rechazamos la hipótesis nula solo si la puntuación t para la muestra es extrema en una dirección que especificamos antes de recolectar los datos. Esta prueba tiene sentido cuando tenemos buenas razones para esperar que la media de la muestra difiera de la hipotética media poblacional en una dirección particular.
Así es como funciona. Cada valor crítico de una cola en Table se\(\PageIndex{1}\) puede interpretar nuevamente como un par de valores: uno positivo y otro negativo. Una puntuación t por debajo del valor crítico inferior se encuentra en el 5% más bajo de la distribución, y una puntuación t por encima del valor crítico superior está en el 5% más alto de la distribución. Para 24 grados de libertad, estos valores son −1.711 y 1.711. (Estos están representados por las líneas verticales verdes en la Figura\(\PageIndex{1}\).) Sin embargo, para una prueba de una cola, debemos decidir antes de recolectar datos si esperamos que la media de la muestra sea menor que la media hipotética de la población, en cuyo caso usaríamos solo el valor crítico inferior, o esperamos que la media muestral sea mayor que la media hipotética de la población, en cuyo caso se usaría sólo el valor crítico superior. Observe que aún rechazamos la hipótesis nula cuando el puntaje t para nuestra muestra está en el 5% más extremo de los puntajes t que esperaríamos si la hipótesis nula fuera cierta, por lo que α permanece en .05. Simplemente hemos redefinido extreme para referirnos solo a una cola de la distribución. La ventaja de la prueba de una cola es que los valores críticos son menos extremos. Si la media de la muestra difiere de la hipotética media poblacional en la dirección esperada, entonces tenemos una mejor oportunidad de rechazar la hipótesis nula. La desventaja es que si la media muestral difiere de la hipotética media poblacional en la dirección inesperada, entonces no hay ninguna posibilidad de rechazar la hipótesis nula.
Las Muestras Dependientes t — Prueba
La prueba t de muestras dependientes (a veces llamada prueba t- de muestras pareadas) se utiliza para comparar dos medias para la misma muestra analizada en dos momentos diferentes o bajo dos condiciones diferentes. Esta comparación es apropiada para diseños pretest-posttest o experimentos dentro de sujetos. La hipótesis nula es que las medias en los dos tiempos o bajo las dos condiciones son las mismas en la población. La hipótesis alternativa es que no son lo mismo. Esta prueba también puede ser de una sola cola si el investigador tiene buenas razones para esperar que la diferencia vaya en una dirección particular.
Ayuda a pensar en la prueba t- de muestras dependientes como un caso especial de la prueba t- de una muestra. Sin embargo, el primer paso en la prueba t- de muestras dependientes es reducir las dos puntuaciones para cada participante a una única puntuación de diferencia tomando la diferencia entre ellos. En este punto, la prueba t- de muestras dependientes se convierte en una prueba t- de una muestra sobre las puntuaciones de diferencia. La hipotética media poblacional (µ 0) de interés es 0 porque así sería la puntuación de diferencia media si no hubiera diferencia en promedio entre los dos tiempos o dos condiciones. Ahora podemos pensar en la hipótesis nula como que la puntuación de diferencia media en la población es 0 (µ 0 = 0) y la hipótesis alternativa como que la puntuación de diferencia media en la población no es 0 (µ 0 ≠ 0).
La prueba t- de muestras independientes
La prueba t- de muestras independientes se utiliza para comparar las medias de dos muestras separadas (M 1 y M 2). Las dos muestras podrían haberse probado en diferentes condiciones en un experimento entre sujetos, o podrían ser grupos preexistentes en un diseño transversal (por ejemplo, mujeres y hombres, extravertidos e introvertidos). La hipótesis nula es que las medias de las dos poblaciones son las mismas: µ 1 = µ 2. La hipótesis alternativa es que no son iguales: µ 1 ≠ µ 2. Nuevamente, la prueba puede ser de una sola cola si el investigador tiene buenas razones para esperar que la diferencia vaya en una dirección particular.
El estadístico t aquí es un poco más complicado porque debe tomar en cuenta dos medias de muestra, dos desviaciones estándar y dos tamaños de muestra. La fórmula es la siguiente:
\[t=\frac{M_{1}-M_{2}}{\sqrt{\frac{S D_{1}^{2}}{n_{1}}+\frac{S D_{2}^{2}}{n_{2}}}}\]
Observe que esta fórmula incluye desviaciones estándar cuadradas (las varianzas) que aparecen dentro del símbolo de raíz cuadrada. Además, n 1 y n 2 minúsculas se refieren a los tamaños de muestra en los dos grupos o condición (a diferencia de N mayúscula, que generalmente se refiere al tamaño total de la muestra). Lo único adicional que hay que saber aquí es que hay N − 2 grados de libertad para la prueba t- de muestras independientes.
El análisis de varianza
Se utilizan pruebas T para comparar dos medias (una media muestral con una media poblacional, la media de dos condiciones o dos grupos). Cuando hay más de dos grupos o medias de condición a comparar, la prueba de hipótesis nula más común es el análisis de varianza (ANOVA). En esta sección, nos fijamos principalmente en el ANOVA unidireccional, que se utiliza para diseños entre sujetos con una sola variable independiente. Luego consideramos brevemente algunas otras versiones del ANOVA que se utilizan para diseños de investigación factorial y dentro de sujetos.
ANOVA de una vía
El ANOVA unidireccional se utiliza para comparar las medias de más de dos muestras (M 1, M 2... M G) en un diseño entre sujetos. La hipótesis nula es que todas las medias son iguales en la población: µ 1 = µ 2 =... = µ G. La hipótesis alternativa es que no todas las medias en la población son iguales.
El estadístico de prueba para el ANOVA se llama F. Se trata de una relación de dos estimaciones de la varianza poblacional con base en los datos de la muestra. Una estimación de la varianza poblacional se denomina cuadrados medios entre grupos (MS B) y se basa en las diferencias entre las medias de la muestra. El otro se denomina cuadrados medios dentro de los grupos (MS W) y se basa en las diferencias entre las puntuaciones dentro de cada grupo. El estadístico F es la relación entre el MS B y el MS W y, por lo tanto, puede expresarse de la siguiente manera:
\[F= \dfrac{MS_B}{MS_W}\]
Nuevamente, la razón por la que F es útil es que sabemos cómo se distribuye cuando la hipótesis nula es cierta. Como se muestra en la Figura\(\PageIndex{2}\), esta distribución es unimodal y sesgada positivamente con valores que se agrupan alrededor de 1. La forma precisa de la distribución depende tanto del número de grupos como del tamaño de la muestra, y hay valores de grados de libertad asociados a cada uno de estos. Los grados de libertad entre grupos es el número de grupos menos uno: df B = (G − 1). Los grados de libertad dentro de los grupos son el tamaño total de la muestra menos el número de grupos: df W = N − G. Nuevamente, conocer la distribución de F cuando la hipótesis nula es verdadera nos permite encontrar el valor p.
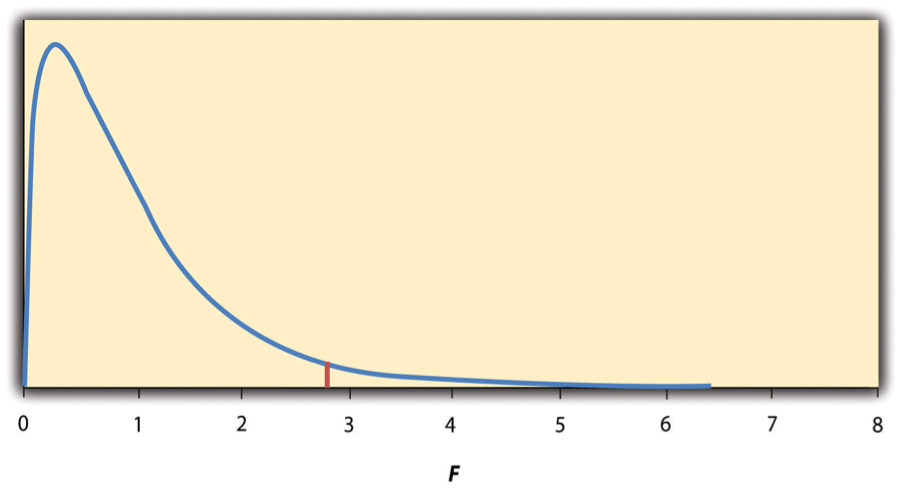
Las herramientas en línea del Capítulo 12 y el software estadístico como Excel y SPSS computarán F y encontrarán el valor p. Si p es igual o menor que .05, entonces rechazamos la hipótesis nula y concluimos que existen diferencias entre las medias grupales en la población. Si p es mayor que .05, entonces conservamos la hipótesis nula y concluimos que no hay evidencia suficiente para decir que hay diferencias. En el improbable caso de que calculáramos F a mano, podemos usar una tabla de valores críticos como Table\(\PageIndex{2}\) para tomar la decisión. La idea es que cualquier relación F mayor que el valor crítico tenga un valor p inferior a .05. Así, si la relación F que calculamos está más allá del valor crítico, entonces rechazamos la hipótesis nula. Si la relación F que calculamos es menor que el valor crítico, entonces conservamos la hipótesis nula.
| df B | |||
| df W | 2 | 3 | 4 |
| 8 | 4.459 | 4.066 | 3.838 |
| 9 | 4.256 | 3.863 | 3.633 |
| 10 | 4.103 | 3.708 | 3.478 |
| 11 | 3.982 | 3.587 | 3.357 |
| 12 | 3.885 | 3.490 | 3.259 |
| 13 | 3.806 | 3.411 | 3.179 |
| 14 | 3.739 | 3.344 | 3.112 |
| 15 | 3.682 | 3.287 | 3.056 |
| 16 | 3.634 | 3.239 | 3.007 |
| 17 | 3.592 | 3.197 | 2.965 |
| 18 | 3.555 | 3.160 | 2.928 |
| 19 | 3.522 | 3.127 | 2.895 |
| 20 | 3.493 | 3.098 | 2.866 |
| 21 | 3.467 | 3.072 | 2.840 |
| 22 | 3.443 | 3.049 | 2.817 |
| 23 | 3.422 | 3.028 | 2.796 |
| 24 | 3.403 | 3.009 | 2.776 |
| 25 | 3.385 | 2.991 | 2.759 |
| 30 | 3.316 | 2.922 | 2.690 |
| 35 | 3.267 | 2.874 | 2.641 |
| 40 | 3.232 | 2.839 | 2.606 |
| 45 | 3.204 | 2.812 | 2.579 |
| 50 | 3.183 | 2.790 | 2.557 |
| 55 | 3.165 | 2.773 | 2.540 |
| 60 | 3.150 | 2.758 | 2.525 |
| 65 | 3.138 | 2.746 | 2.513 |
| 70 | 3.128 | 2.736 | 2.503 |
| 75 | 3.119 | 2.727 | 2.494 |
| 80 | 3.111 | 2.719 | 2.486 |
| 85 | 3.104 | 2.712 | 2.479 |
| 90 | 3.098 | 2.706 | 2.473 |
| 95 | 3.092 | 2.700 | 2.467 |
| 100 | 3.087 | 2.696 | 2.463 |
Elaboraciones de ANOVA
Comparaciones Post Hoc
Cuando rechazamos la hipótesis nula en un ANOVA unidireccional, concluimos que las medias grupales no son todas iguales en la población. Pero esto puede indicar cosas diferentes. Con tres grupos, puede indicar que las tres medias son significativamente diferentes entre sí. O puede indicar que uno de los medios es significativamente diferente de los otros dos, pero los otros dos no son significativamente diferentes entre sí. Podría ser, por ejemplo, que las estimaciones calóricas medias de las carreras de psicología, las carreras de nutrición y los dietistas sean significativamente diferentes entre sí. O podría ser que la media para los dietistas sea significativamente diferente de los medios para las carreras de psicología y nutrición, pero los medios para las carreras de psicología y nutrición no son significativamente diferentes entre sí. Por esta razón, los resultados de ANOVA unidireccional estadísticamente significativos suelen ser seguidos con una serie de comparaciones post hoc de pares seleccionados de medias grupales para determinar cuáles son diferentes de cuáles otros.
Un enfoque para las comparaciones post hoc sería realizar una serie de pruebas t- de muestras independientes comparando la media de cada grupo con cada una de las medias del otro grupo. Pero hay un problema con este enfoque. En general, si realizamos una prueba t cuando la hipótesis nula es verdadera, tenemos un 5% de probabilidad de rechazar erróneamente la hipótesis nula (ver Sección 13.3 “Consideraciones adicionales” para más información sobre dichos errores de Tipo I). Si realizamos varias pruebas t- cuando la hipótesis nula es verdadera, la posibilidad de rechazar erróneamente al menos una hipótesis nula aumenta con cada prueba que realizamos. Por lo tanto, los investigadores no suelen hacer comparaciones post hoc utilizando pruebas t estándar porque existe una posibilidad demasiado grande de que rechacen erróneamente al menos una hipótesis nula. En cambio, utilizan uno de varios procedimientos de prueba t modificados, entre ellos el procedimiento de Bonferonni, la prueba de diferencia menos significativa de Fisher (LSD) y la prueba de diferencia honestamente significativa de Tukey (HSD). Los detalles de estos enfoques están más allá del alcance de este libro, pero es importante entender su propósito. Es para mantener el riesgo de rechazar erróneamente una verdadera hipótesis nula a un nivel aceptable (cercano al 5%).
ANOVA de medidas repetidas
Recordemos que el ANOVA unidireccional es apropiado para diseños entre sujetos en los que las medias que se comparan provienen de grupos separados de participantes. No es apropiado para diseños dentro de sujetos en los que las medias que se comparan provienen de los mismos participantes probados en diferentes condiciones o en diferentes momentos. Esto requiere un enfoque ligeramente diferente, llamado ANOVA de medidas repetidas. Los fundamentos del ANOVA de medidas repetidas son los mismos que para el ANOVA unidireccional. La principal diferencia es que medir la variable dependiente varias veces para cada participante permite una medida más refinada de MS W. Imagínese, por ejemplo, que la variable dependiente en un estudio es una medida del tiempo de reacción. Algunos participantes serán más rápidos o lentos que otros debido a diferencias individuales estables en sus sistemas nerviosos, músculos y otros factores. En un diseño entre sujetos, estas diferencias individuales estables simplemente se sumarían a la variabilidad dentro de los grupos y aumentarían el valor de MS W (lo que, a su vez, disminuiría el valor de F). Sin embargo, en un diseño dentro de los sujetos, estas diferencias individuales estables pueden medirse y restarse del valor de MS W. Este menor valor de MS W significa un mayor valor de F y una prueba más sensible.
ANOVA factorial
Cuando se incluye más de una variable independiente en un diseño factorial, el enfoque apropiado es el ANOVA factorial. Nuevamente, los fundamentos del ANOVA factorial son los mismos que para los ANOVA unidireccionales y de medidas repetidas. La principal diferencia es que produce una relación F y un valor p para cada efecto principal y para cada interacción. Volviendo a nuestro ejemplo de estimación calórica, imagínese que el psicólogo de la salud prueba el efecto del participante mayor (psicología vs. nutrición) y tipo de alimento (galleta vs. hamburguesa) en un diseño factorial. Un ANOVA factorial produciría relaciones F separadas y valores p para el efecto principal de mayor, el efecto principal del tipo de alimento y la interacción entre mayor y alimento. Se deben realizar modificaciones apropiadas dependiendo de si el diseño es entre sujetos, dentro de los sujetos o mixto.
Prueba de coeficientes de correlación
Para las relaciones entre variables cuantitativas, donde se usa r de Pearson (el coeficiente de correlación) para describir la fuerza de esas relaciones, la prueba de hipótesis nula apropiada es una prueba del coeficiente de correlación. La lógica básica es exactamente la misma que para otras pruebas de hipótesis nulas. En este caso, la hipótesis nula es que no hay relación en la población. Podemos usar el griego rho minúscula (ρ) para representar el parámetro relevante: ρ = 0. La hipótesis alternativa es que existe una relación en la población: ρ ≠ 0. Al igual que con la prueba t, esta prueba puede ser de dos colas si el investigador no tiene expectativas sobre la dirección de la relación o de una cola si el investigador espera que la relación vaya en una dirección particular.
Es posible utilizar el coeficiente de correlación para la muestra para calcular una puntuación t con N − 2 grados de libertad y luego proceder como para una prueba t-. Sin embargo, por la forma en que se calcula, el coeficiente de correlación también puede tratarse como su propio estadístico de prueba. Las herramientas estadísticas en línea y el software estadístico como Excel y SPSS generalmente calculan el coeficiente de correlación y proporcionan el valor p asociado a ese valor. Como siempre, si el valor p es igual o menor que .05, rechazamos la hipótesis nula y concluimos que existe una relación entre las variables en la población. Si el valor de p es mayor que .05, conservamos la hipótesis nula y concluimos que no hay evidencia suficiente para decir que hay una relación en la población. Si calculamos el coeficiente de correlación a mano, podemos usar una tabla como Table\(\PageIndex{4}\), que muestra los valores críticos de r para varios tamaños de muestras cuando α es .05. Un valor muestral del coeficiente de correlación que es más extremo que el valor crítico es estadísticamente significativo.
| Valor crítico de r | ||
|---|---|---|
| N | De una cola | Dos colas |
| 5 | .805 | .878 |
| 10 | .549 | .632 |
| 15 | .441 | .514 |
| 20 | .378 | .444 |
| 25 | .337 | .396 |
| 30 | .306 | .361 |
| 35 | .283 | .334 |
| 40 | .264 | .312 |
| 45 | .248 | .294 |
| 50 | .235 | .279 |
| 55 | .224 | .266 |
| 60 | .214 | .254 |
| 65 | .206 | .244 |
| 70 | .198 | .235 |
| 75 | .191 | .227 |
| 80 | .185 | .220 |
| 85 | .180 | .213 |
| 90 | .174 | .207 |
| 95 | .170 | .202 |
| 100 | .165 | .197 |


