6.3: Derivadas de Funciones Exponenciales

Las funciones exponenciales y la tasa de cambio se utilizan para modelar muchas situaciones del mundo real, como el crecimiento de la población, la desintegración de la vida media radiactiva, la atenuación de las señales electromagnéticas en los medios y las transacciones financieras. ¿Sabes escribir ecuaciones exponenciales generales para el crecimiento de una población que se duplica cada 5 años, y su tasa de cambio?

---

Derivadas de Funciones Exponenciales

Una función exponencial$f(x) \nonumber$ tiene la forma:

$$f(x) = b^x \nonumber$$

donde b se llama la base y es un número positivo, real.

La siguiente figura muestra algunas gráficas de función exponencial para 0<b≤10. Es muy claro que el signo de la derivada de un exponencial depende del valor de b. Si 0<b<1, el valor de la derivada de la función (pendiente de la línea tangente) será negativo porque la función siempre va disminuyendo a medida que x aumenta. Para b>1, la derivada de la función siempre será positiva porque la función aumenta a medida que aumenta x.

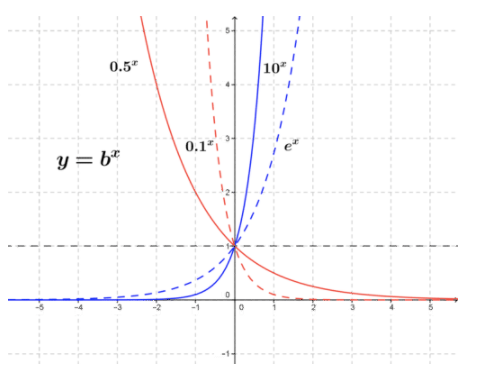
CC BY-NC-SA

Pero, ¿cuál es la derivada de una función exponencial? Podemos tomar los siguientes pasos para encontrar una expresión para$\frac{d}{dx}[bx] \nonumber$ usando la definición de la derivada:

$\displaystyle \frac{d}{dx}[bx]= \lim_{h \to 0} \frac{b^{x+h}−b^x}{h} \nonumber$... Definición límite de la derivada

$= \lim_{h \to 0} \frac{b^xb^h−b^x}{h} \nonumber$... Propiedad exponente

$= \lim_{h \to 0} \frac{b^h−1}{h}⋅b^x \nonumber$... Factoring

$= ( \lim_{h→0} \frac{b^h−1}{h})⋅bx \nonumber$... Límite de propiedad de un producto

El resultado anterior muestra$\frac{d}{dx}[bx] \nonumber$ depende del producto$\lim_{h→0} \frac{b^h−1}{h} \nonumber$ y de la función original. Pero ¿qué es$\lim_{h→0} \frac{b^h−1}{h} \nonumber$? Hay varias formas de evaluar este límite, pero por ahora echemos un vistazo rápido al comportamiento de$\frac{b^h−1}{h} \nonumber$. Esta función se representa a continuación para un número de valores de b , y el límite a$h=0 \nonumber$ se indica por los puntos A-E.

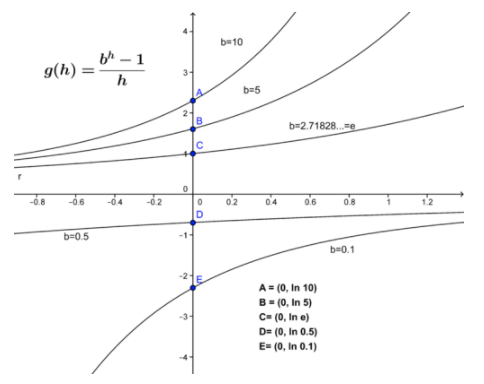
CC BY-NC-SA

Si bien no es del todo obvio:$\lim_{h→0} \frac{b^h−1}{h} = ln(b) \nonumber$. ¿Recuerdas la función de logaritmo natural$y=lnx \nonumber$ en tu calculadora? El logaritmo natural es la función logaritmo general con base$b=e=2.71828 \nonumber$...

Dada la función exponencial$f(x)=b^x \nonumber$, donde la base b es un número positivo, real, entonces la representación general de la derivada de una función exponencial es:

$$\frac{d}{dx}[bx]=lnb⋅b^x \nonumber$$

Añadiendo la Regla de Cadena a la definición, dada la función exponencial f (x) =bu, donde u=g (x) y g (x) es una función diferenciable, entonces:

$$\frac{d}{dx}[bu]=(lnb⋅b^u) \frac{du}{dx} \nonumber$$

---

Ejemplos

Ejemplo 1

Anteriormente, se le preguntó cuál es la ecuación exponencial general para el crecimiento de una población que se duplica cada 5 años es.

Una población$P(t) \nonumber$ que se duplica cada 5 años podría modelarse como$P(t)=P_02^{\frac{t}{5}} \nonumber$, donde la variable t representa número de años desde que la población estaba en un nivel de$P_0 \nonumber] \nonumber$. ¿Pudiste determinar que la tasa de cambio de$P(t) \nonumber$ es$P′(t) = \frac{P_0 ln2}{5}⋅2^{\frac{t}{5}} \nonumber$?

Ejemplo 2

Dado$y=500⋅0.7^x \nonumber$, ¿qué es$\frac{dy}{dx} \nonumber$?

$$\frac{dy}{dx}=\frac{d}{dx}[500⋅0.7^x] \nonumber$$

$$= 500 \frac{d}{dx}[0.7^x] \nonumber$$

$= 500[ln(0.7)⋅0.7^x] \nonumber$... Usa tu calculadora para encontrar ln (0.7)

$$=−178.3⋅0.7^x \nonumber$$

De ahí que$\frac{dy}{dx} =−178.3⋅0.7^x \nonumber$, y como se esperaba, las pendientes de todas las líneas tangentes sean negativas.

Hay un caso especial importante que debes conocer

Ejemplo 3

Dado$y=500⋅e^x \nonumber$, ¿qué es$\frac{dy}{dx} \nonumber$?

$$\frac{dy}{dx}= \frac{d}{dx}[500⋅ex] \nonumber$$

$$= 500 \frac{d}{dx}[ex] \nonumber$$

$\frac{dy}{dx}=500[ln(e)⋅ex] \nonumber$... Usa tu calculadora para encontrar ln (e)

$$= \frac{d}{dx}[500⋅ex] \nonumber$$

$$=500[1⋅ex] \nonumber$$

$$=500⋅ex \nonumber$$

De ahí$\frac{dy}{dx}=500⋅ex \nonumber$,, y esta es solo la función original. Esta función exponencial, con base e, es especial: la tasa de cambio (o pendiente de la línea tangeta) en cualquier punto es igual al valor de la función en ese punto.

Ejemplo 4

Dado$y=10⋅2.5−3x^2 \nonumber$, ¿qué es$\frac{dy}{dx} \nonumber$?

$$\frac{dy}{dx} = \frac{d}{dx}[10⋅2.5−3x2] \nonumber$$

$$=10 \frac{d}{dx}[2.5−3x2] \nonumber$$

$$=10⋅ln(2.5)⋅2.5−3x2⋅ddx[−3x^2] \nonumber$$

$$=10⋅(0.9162)⋅2.5−3x^2⋅[−6x] \nonumber$$

$$=−55x⋅2.5−3x^2 \nonumber$$

Por lo tanto,$\frac{dy}{dx} =−55x⋅2.5−3x^2 \nonumber$

Ejemplo 5

Dado$y=500⋅e−2x⋅cos(5πx) \nonumber$, ¿qué es$\frac{dy}{dx} \nonumber$?

$$\frac{dy}{dx}= \frac{d}{dx}[500⋅e−2x⋅cos(5πx)] \nonumber$$

$=500⋅[ \frac{d}{dx}(e−2x)⋅cos(5πx)+e−2x⋅ \frac{d}{dx}(cos(5πx))] \nonumber$... Regla del producto

$=500⋅[ln(e)⋅e−2x \frac{d}{dx}(−2x)⋅cos(5πx)+e−2x⋅(−sin(5πx)⋅ \frac{d}{dx}(5πx))] \nonumber$... Usar regla de cadena

$=500⋅[(1)⋅e−2x⋅(−2)⋅cos(5πx)+e−2x⋅(−sin(5πx)⋅5π)] \nonumber$... Simplificar.

$=−500⋅e−2x[2⋅cos(5πx)+5πsin(5πx)] \nonumber$... Simplificar

Por lo tanto,$\frac{dy}{dx} =−500⋅e−2x[2⋅cos(5πx)+5πsin(5πx)] \nonumber$.

---

Revisar

Para #1 -14, encuentra la derivada.

1. $y=7^x \nonumber$
2. $y=3^{2x} \nonumber$
3. $y=5^x−3x^2 \nonumber$
4. $y=2^{x^2} \nonumber$
5. $y=e^{x^2} \nonumber$
6. $f(x)= \frac{1}{ \sqrt{πσ}}e^{−αk(x−x0)^2} \nonumber$donde σ, α, x0 y k son constantes y σ≠ 0.
7. $y=e^{6x} \nonumber$
8. $y=e^{3x^3}−2x^2+6 \nonumber$
9. $y=\frac{e^x−e−x}{e^x+e−x} \nonumber$
10. $y=cos(e^x) \nonumber$
11. $y=e^{−x}3^x \nonumber$
12. $y=3^{−x^2+2x+1} \nonumber$
13. $y=2^x3^x \nonumber$
14. $y=e^{−x}sinx \nonumber$
15. Encuentra una ecuación de la línea tangente a$f(x)=x^3+2e^x \nonumber$ en el punto (0, 2).

---

Reseña (Respuestas)

Para ver las respuestas de Revisar, abra este archivo PDF y busque la sección 3.9.

---

El vocabulario

Término	Definición
derivado	La derivada de una función es la pendiente de la línea tangente a la función en un punto dado de la gráfica. Las notaciones para derivadas incluyen f′ (x), dydx, y′, dfdx y\ frac {df (x)} {dx}.
Función exponencial	Una función exponencial es una función cuya variable está en el exponente. La forma general es$y=a⋅b^{x−h}+k \nonumber$.

---

Recursos adicionales