7.4: Segunda Prueba Derivada
- Page ID
- 105813
La derivada de una curva de función en un punto es la analogía matemática a nuestra determinación visual si la función está aumentando o disminuyendo en el punto. Pero si miras una curva de función, también puedes determinar visualmente si las líneas tangentes se están volviendo más verticales o más horizontales a lo largo de un intervalo. El reconocimiento visual de esta tasa de cambio de la pendiente es una medida de curvatura (o concavidad), que a su vez puede indicarle específicamente qué tipo de extremos están presentes. La representación matemática de la tasa de cambio de la pendiente es la segunda derivada, la cual se utiliza para identificar tipos de curvatura. ¿Cuál es la relación entre la segunda derivada y la concavidad?
Prueba de Concavidad y Segunda Derivada
Existe una propiedad sobre la forma, o curvatura, de una gráfica llamada concavidad, que ayudará a identificar con precisión los intervalos donde una función está aumentando o disminuyendo, donde se ubican los máximos y mínimos, y también ayudará a bosquejar la gráfica. La concavidad es la dirección en la que se abre la curva.
El tipo de concavidad en una curva se define de la siguiente manera:
Se dice que una función f es cóncava hacia arriba en [a, b] contenida en el dominio de f si f′ es una función creciente en [a, b] y cóncava hacia abajo en [a, b] si f′ es una función decreciente en [a, b].
Aquí hay una función que ilustra estas propiedades.
Considera la función\( f(x)=x^3−x \nonumber\):
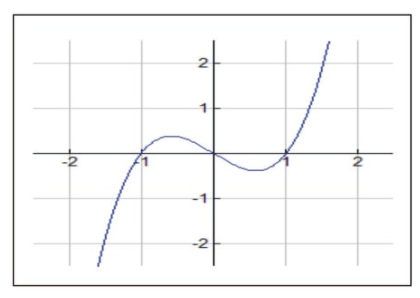
CC BY-NC-SA
Ya que\( f(x)=x^3−x=x(x^2−1) \nonumber\), la función tiene ceros en x=±1,0.
También,\( f′(x)=0=3x^2−1 \nonumber\), nos dice la ubicación de los extremos: un máximo relativo a\( x=− \frac{ \sqrt{3}}{3} \nonumber\) y un mínimo relativo a\( x= \frac{ \sqrt{3}}{3} \nonumber\).
Tenga en cuenta que la gráfica parece ser cóncava hacia abajo para todos los intervalos en (−∞ ,0) y cóncava hacia arriba para todos los intervalos en (0, +∞). ¿Dónde crees que la concavidad de la gráfica cambió de cóncava hacia abajo a cóncava hacia arriba? Si respondiste a x=0 estarías en lo correcto.
En general, deseamos identificar no sólo los extremos de una función sino también los puntos donde la gráfica cambia de concavidad. Un punto en una gráfica de una función f donde cambia la concavidad se denomina punto de inflexión.
El problema anterior solo tenía un punto de inflexión. Pero fácilmente podemos llegar a ejemplos de funciones donde hay más de un punto de inflexión.
Considera la función\( f(x)=x^4−3x^3+x−2 \nonumber\) que se muestra en la figura.
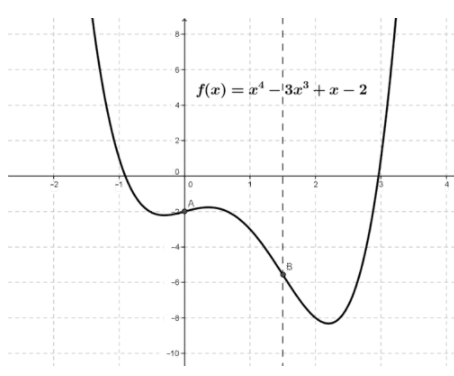
CC BY-NC-SA
Podemos ver que la gráfica tiene dos mínimos relativos, un máximo relativo y dos puntos de inflexión (a A y B).
En general podemos utilizar la siguiente prueba para la concavidad:
Supongamos que f es continuo en [a, b] y que I es algún intervalo abierto en el dominio de f.
- Si f′′ (x) >0 para todos los xi, entonces la gráfica de f es cóncava hacia arriba en I
- Si f′′ (x) <0 para todos los xi, entonces la gráfica de f es cóncava hacia abajo en I
Apliquemos la prueba de concavidad a la función\( f(x)=x^4−3x^3+x−2 \nonumber\):
La segunda derivada es,\( f′′(x)=12x^2−18x=6x(2x−3) \nonumber\), y la concavidad se da en la tabla.
|
Intervalo o punto |
f′′ (x) |
Concavidad |
|
[-1,0) |
>0 |
Al alza |
|
0 |
=0 |
Cambio=Inflexión |
|
(0, 1.5) |
<0 |
A la baja |
|
1.5 |
=0 |
Cambio=Inflexión |
|
(1.5, 3] |
>0 |
Al alza |
¿Se ve cómo la concavidad da una pista sobre la presencia de un punto relativo máximo, o mínimo, o de inflexión? Una consecuencia de la prueba de concavidad es la siguiente prueba para identificar dónde tenemos extremos y puntos de inflexión de f.
La Prueba de Segunda Derivada para Extrema es la siguiente:
Supongamos que f es una función continua cerca de c y que c es un valor crítico de f Entonces
- Si f′′ (c) <0, entonces f tiene un máximo relativo en x=c.
- Si f′′ (c) >0, entonces f tiene un mínimo relativo en x=c.
- Si f′′ (c) =0, entonces la prueba no es concluyente y x=c puede ser un punto de inflexión.
¿Funciona la prueba para nuestro ejemplo anterior de\( f(x)=x^4−3x^3+x−2 \nonumber\)?
Podemos encontrar los valores críticos donde\( f′(x)=4x^3−9x^2+1=0 \nonumber\), y utilizarlos para evaluar f′′ (c). A continuación se muestran los resultados.
|
Punto Crítico |
f′′ (c) |
Conclusión |
|
x=−0.312 |
>0 |
Mínimo Relativo |
|
x=0.364 |
<0 |
Máximo Relativo |
|
x=2.198 |
>0 |
Mínimo Relativo |
Las pruebas funcionan sobre esta función.
Recuerde, sin embargo, que la Prueba de Segunda Derivada nos advierte que si f′′ (c) =0, la prueba no es concluyente, porque c puede ser un punto de inflexión. Recordemos que así fue el caso\( f(x)=x^3 \nonumber\).
Ejemplos
Ejemplo 1
Anteriormente, se le preguntó qué relación existe entre la curvatura de una función y la segunda derivada. La curvatura de una gráfica de funciones se puede describir por su concavidad (arriba o abajo), que a su vez puede ser determinada en cada punto por la segunda derivada (si se define). Porque los puntos críticos pueden determinar las ubicaciones de máximos o mínimos relativos sin identificar cuáles, conocer el tipo de curvatura de la segunda derivada puede identificar específicamente si tenemos un mínimo o un máximo, o ninguno.
Ejemplo 2
Considera la función\( f(x)=x+ \frac{4}{x} \nonumber\). Encuentre los puntos críticos y determine si son máximos relativos o mínimos relativos usando la Prueba de Segunda Derivada.
Lo primero que hay que notar es que la función no está definida en x=0.
Para encontrar los puntos críticos buscamos puntos c donde f′ (c) =0.
\) f′ (x) =1−\ frac {4} {x^2} =0\ nonumber\) significa que hay puntos críticos en x=−2, y x=2.
Dado que\( f′′(x)= \frac{8}{x^3} :f′′(−2)=−1 \nonumber\) y la curva es cóncava hacia abajo con un máximo relativo; f′′ (2) =1, y la curva es cóncava hacia arriba con un mínimo relativo.
El gráfico de funciones es como se muestra.
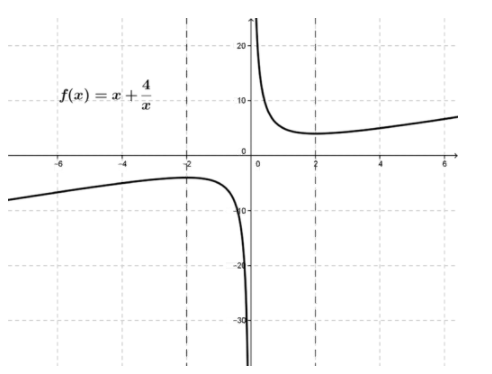
CC BY-NC-SA
Revisar
- Encuentra todos los extremos usando la Prueba de Segunda Derivada:\( f(x)= \frac{x^2}{4}+ \frac{4}{x} \nonumber\).
- Considerar\( f(x)= x^2+ax+b \nonumber\), con f (1) =3.
- Determinar a y b para que x=1 sea un valor crítico de la función f.
- ¿El punto (1, 3) es un máximo, un mínimo o ninguno?
Para #3 -6, encuentra todos los extremos y puntos de inflexión. Esbozar la gráfica.
- \( f(x)=x^3+x^2 \nonumber\)
- \( f(x)= \frac{x^2+3}{x} \nonumber\)
- \( f(x)=x^3−12x \nonumber\)
- \( f(x)=− \frac{1}{4}x^4+2x^2 \nonumber\)
- Use su calculadora gráfica para examinar la gráfica de\( f(x)=x(x−1)^3 \nonumber\) (Pista: necesitará cambiar el rango y en la ventana de visualización)
- Discutir la concavidad de la gráfica en el intervalo\( (0, \frac{1}{2}) \nonumber\).
- Usa tu calculadora para encontrar el valor mínimo de la función en el intervalo.
- Verdadero o Falso: ¿\( f(x)=x^4+4x^3 \nonumber\)tiene un mínimo relativo en x=−2 y un máximo relativo en x=0?
- Si es posible, proporcione un ejemplo de una función no polinómica que tenga exactamente un mínimo relativo.
- Si es posible, proporcione un ejemplo de una función no polinómica que sea cóncava hacia abajo en todas partes en su dominio.
- Sea f (x) una función continua y que [a, b] sea un intervalo cerrado sobre el cual se define f (x). Si sabemos que f (x) es positivo en el intervalo [a, b], ¿nos dice esto algo sobre la concavidad de f (x) sobre [a, b]?
- ¿La función f (x) =x4 es cóncava hacia arriba o hacia abajo en el intervalo [10, 11]?
- ¿La función f (x) =−cos (x) es cóncava hacia arriba o hacia abajo en el intervalo\( [ \frac{π}{2}, \frac{3π}{2}] \nonumber\)?
- Si la primera derivada de f (x) es\( f′(x)=20^xsin(π^x) \nonumber\), ¿f (x) es cóncava hacia arriba o hacia abajo en el intervalo\( [0, \frac{1}{2}] \nonumber\)?
- ¿Qué es un punto de inflexión de la función\( f(x)=4x^3+3x^2+2x+1 \nonumber\)?
- Utilice la prueba de la segunda derivada para clasificar los extremos de la función\( f(x)=x^3+x^2−5ln(x) \nonumber\) a lo largo del intervalo\( (\frac{1}{2},2) \nonumber\).
- Utilice la prueba de la segunda derivada para clasificar los extremos de la función\( f(x)=5^{sin(x)} \nonumber\) a lo largo del intervalo\( (\frac{π}{4}, \frac{3π}{4}) \nonumber\).
- Utilice la prueba de la segunda derivada para clasificar los extremos de la función\( f(x)=ln(2x+x^2) \nonumber\) a lo largo del intervalo\( (−\frac{5}{2},− \frac{1}{2}) \nonumber\).
- Utilice la prueba de la segunda derivada para clasificar los extremos de la función a\( f(x)=x^4 \nonumber\) lo largo del intervalo (1, 5).
- ¿Podemos usar la segunda prueba derivada para verificar si x=0 es un máximo o un mínimo de la función\( f(x)=x^{10}+25 \nonumber\)?
Reseña (Respuestas)
Para ver las respuestas de Revisar, abra este archivo PDF y busque la sección 4.5.
El vocabulario
| Término | Definición |
|---|---|
| cóncavo hacia abajo | Se dice que una función f es cóncava hacia abajo en [a, b] si f′ es una función decreciente en [a, b]. |
| cóncavo hacia arriba | Se dice que una función f es cóncava hacia arriba en [a, b] contenida en el dominio de f si f′ es una función creciente en [a, b]. |
| concavidad | La concavidad describe el comportamiento de la pendiente de la línea tangente de una función de tal manera que la concavidad es positiva si la pendiente está aumentando, negativa si la pendiente es decreciente, y cero si la pendiente es constante. |
| punto de inflexión | Un punto de inflexión es un punto en el dominio donde la concavidad cambia de positiva a negativa o negativa a positiva. |
| prueba de segunda derivada | La segunda prueba derivada dice que si f es una función continua cerca de c y c es un valor crítico de f, entonces si f′′ (c) = 0 <0 then f has a relative maximum at x=c, if f′′ (c) > entonces f tiene un mínimo relativo a x=c, y si f′′ (c) =0 entonces la prueba no es concluyente y x=c puede ser un punto de inflexión. |

