1.9: Medición de ángulos
- Page ID
- 107653
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Medición de ángulos con los protractores y el Postulado de Adición de Ángulo.
Ángulos
Se forma un ángulo cuando dos rayos tienen el mismo punto final. El vértice es el punto final común de los dos rayos que forman un ángulo. Los lados son los dos rayos que forman un ángulo.
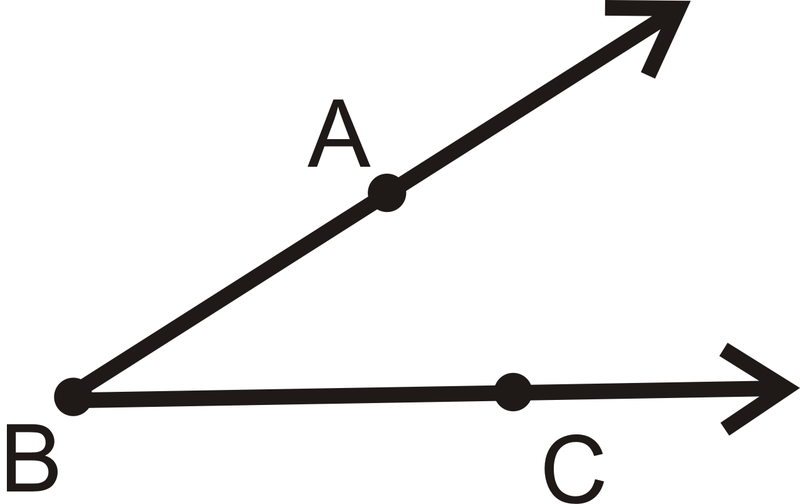Figura\(\PageIndex{1}\)| Etiquetarlo | Dilo |
|---|---|
| \(\angle ABC\) | Ángulo\(ABC\) |
| \(\angle CBA\) | Ángulo\(CBA\) |
El vértice es\(B\) y los lados son\(\overrightarrow{BA}\) y\(\overrightarrow{BC}\). Siempre use tres letras para nombrar un ángulo,\(\angle\) LADO-VERTEX-LADO.
Los ángulos se miden con algo llamado un transportador. Un transportador es un dispositivo de medición que mide qué tan “abierto” es un ángulo. Los ángulos se miden en grados y se etiquetan con un\( ^{\circ}\) símbolo. Por ahora, los ángulos son siempre positivos.
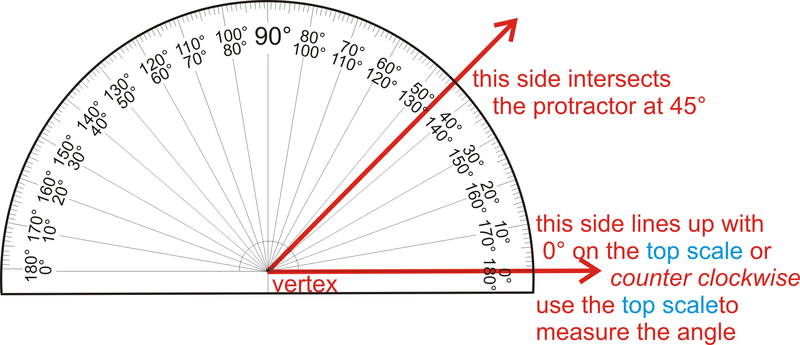Figura\(\PageIndex{2}\)Hay dos conjuntos de medidas, uno que comienza a la izquierda y el otro en el lado derecho del transportador. Ambos van de\( 0 ^{\circ}\) a\(180 ^{\circ}\). Al medir ángulos, puede alinear un lado con\( 0 ^{\circ}\), y ver donde el otro lado golpea el transportador. El vértice se alinea en el medio de la línea de fondo.
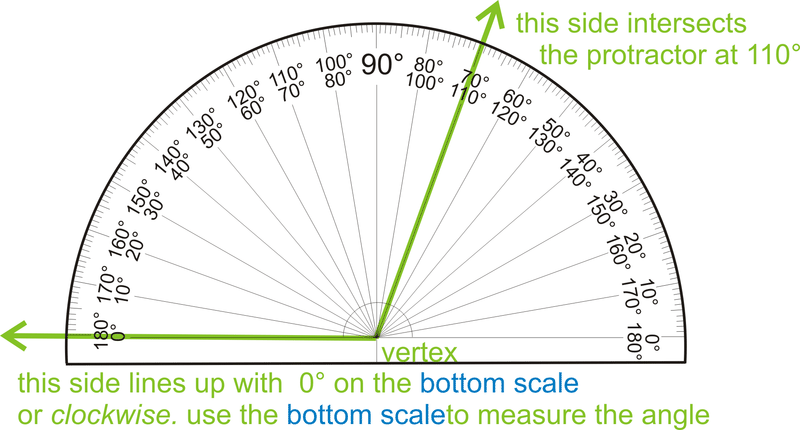Figura\(\PageIndex{3}\)Tenga en cuenta que si no alinea un lado con\( 0 ^{\circ}\), la medida del ángulo será la diferencia de los grados donde los lados del ángulo se cruzan con el transportador.
A veces querrás dibujar un ángulo que sea un número específico de grados. Siga los pasos a continuación para dibujar un\( 50 ^{\circ}\) ángulo con un transportador:
- Comienza dibujando una línea horizontal a través de la página, 2 de largo.
Figura\(\PageIndex{4}\)- Coloca un punto final en el lado izquierdo de tu línea.
- Coloque el transportador en este punto, de tal manera que la línea pase por la\( 0 ^{\circ}\) marca en el transportador y el punto final esté en el centro. Marcar\( 50 ^{\circ}\) en la escala apropiada.
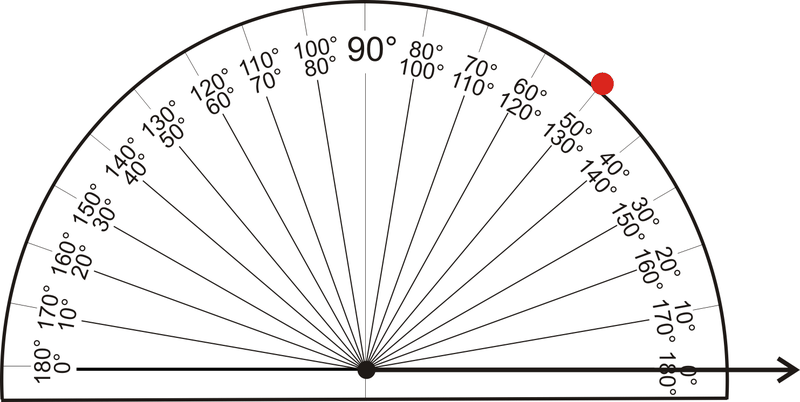Figura\(\ PageIndex {5}\)- Retire el transportador y conecte el vértice y el\(50 ^{\circ}\) mark.
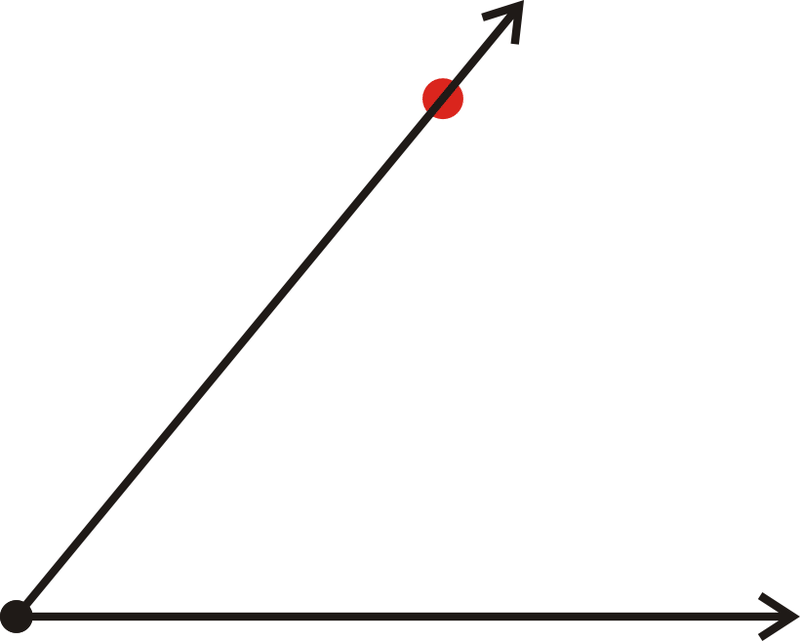Figure \(\PageIndex{6}\)This process can be used to draw any angle between \(0 ^{\circ}\) and \(180 ^{\circ}\).
When two smaller angles form to make a larger angle, the sum of the measures of the smaller angles will equal the measure of the larger angle. This is called the Angle Addition Postulate. So, if B is on the interior of \(\angle ADC\), then
\(\angle ADC = m \angle ADB + \angle BDC\)
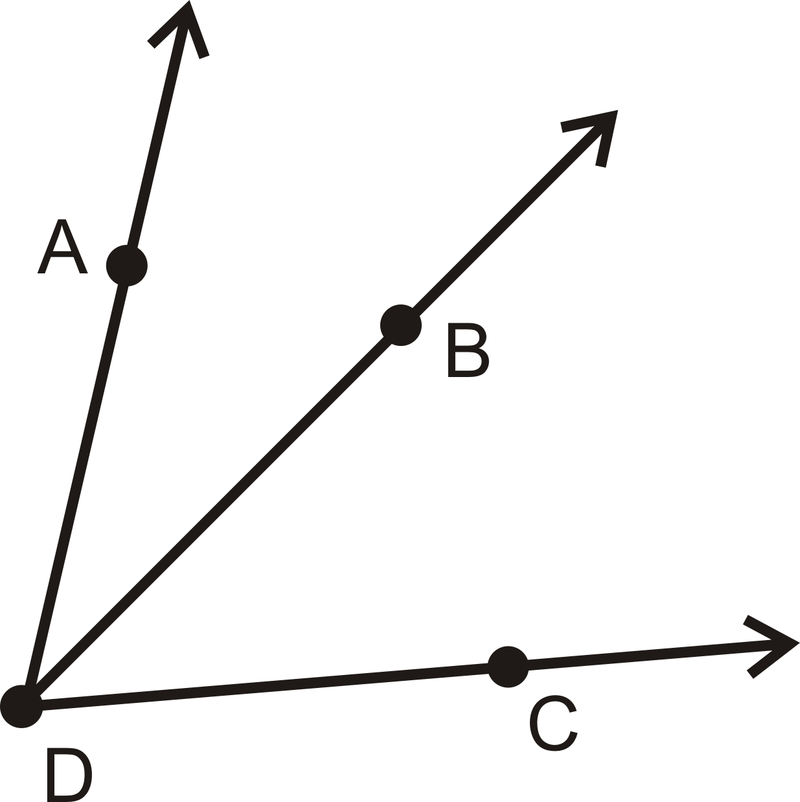Figure \(\PageIndex{7}\)Example \(\PageIndex{1}\)
How many angles are in the picture below? Label each one.
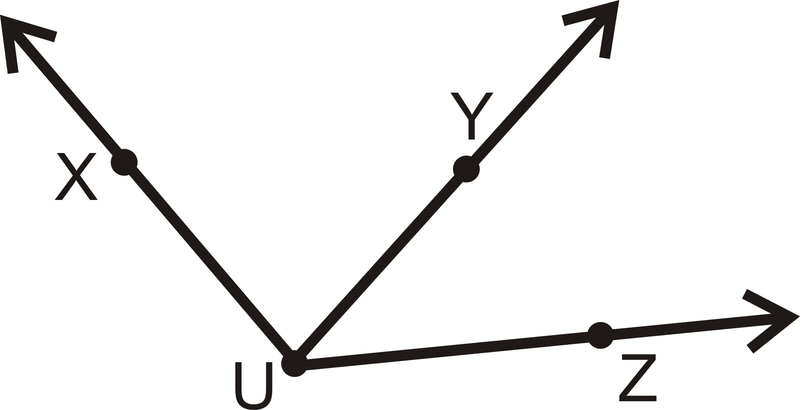Figure \(\PageIndex{8}\)Solution
There are three angles with vertex \(U\). It might be easier to see them all if we separate them.
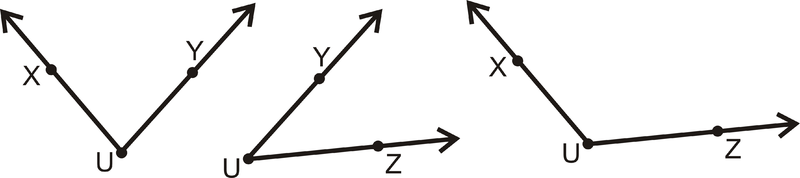Figure \(\PageIndex{9}\)So, the three angles can be labeled, ( \(\angle XUY\) or \(\angle YUX\)), \(\angle YUZ\) (or \(\angle ZUY\)), and \(\angle XUZ\) (or \(\angle ZUX\)).
Example \(\PageIndex{2}\)
Measure the three angles from Example 1, using a protractor.
Figure \(\PageIndex{10}\)Solution
Just like in Example 1, it might be easier to measure these three angles if we separate them.
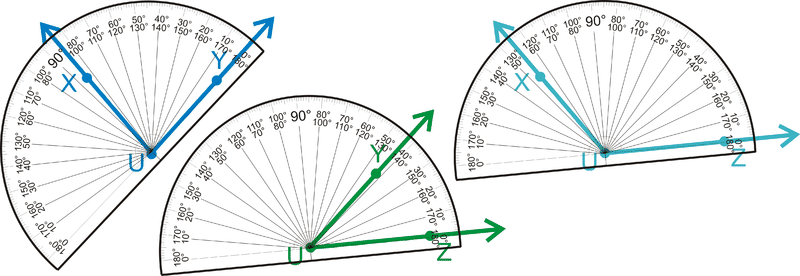Figure \(\PageIndex{11}\)With measurement, we put an m in front of the \(\angle\) sign to indicate measure. So, \(m \angle XUY = 84^{\circ}\), \(m \angle YUZ = 42^{\circ}\) and \(m \angle XUZ = 126^{\circ}\).
Example \(\PageIndex{3}\)
What is the measure of the angle shown below?
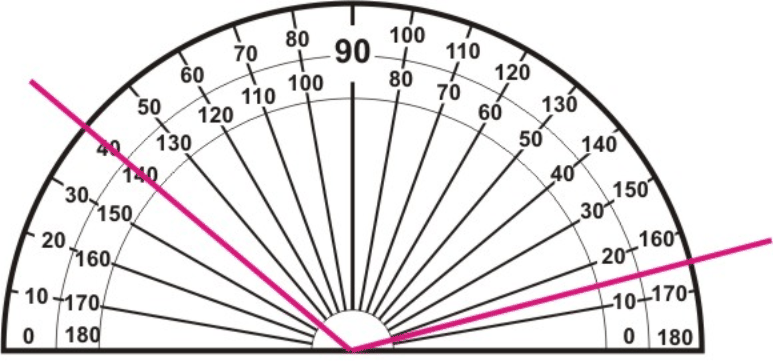Figure \(\PageIndex{12}\)Solution
This angle is not lined up with 0∘, so use subtraction to find its measure. It does not matter which scale you use, as long as you are consistent.
Inner scale: \(140^{\circ} - 15 ^{\circ} = 125 ^{\circ}\)
Outer scale: \(165^{\circ} - 40 ^{\circ} = 125 ^{\circ}\)
Example \(\PageIndex{4}\)
Use a protractor to measure \(\angle RST\) below.
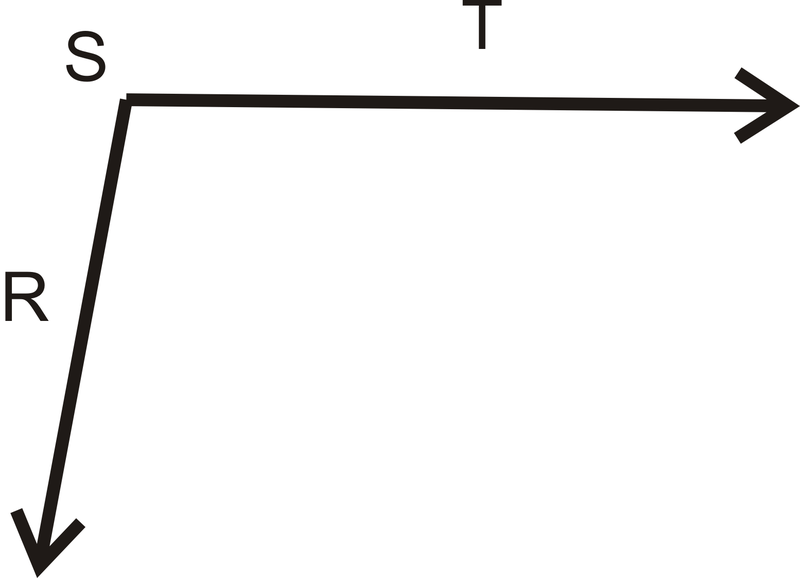Figure \(\PageIndex{13}\)Solution
Lining up one side with \(0 ^{\circ}\) on the protractor, the other side hits \(100 ^{\circ}\).
Example \(\PageIndex{5}\)
What is \(m \angle QRT\) in the diagram below?
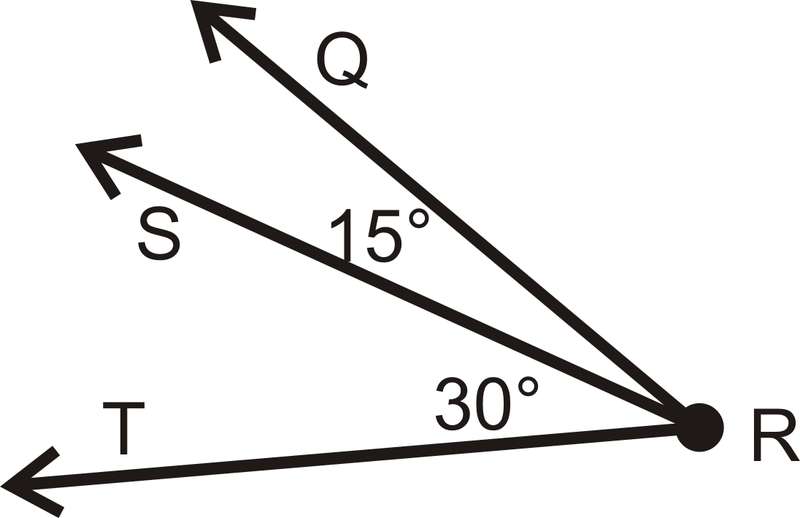Figure \(\PageIndex{14}\)Solution
Using the Angle Addition Postulate, \(m\angle QRT = 15^{\circ}+30^{\circ}=45^{\circ}\).
Review
1. What is \(m \angle LMN\) if \(m \angle LMO = 85^{\circ}\) and \(m \angle NMO = 53^{\circ}\)?
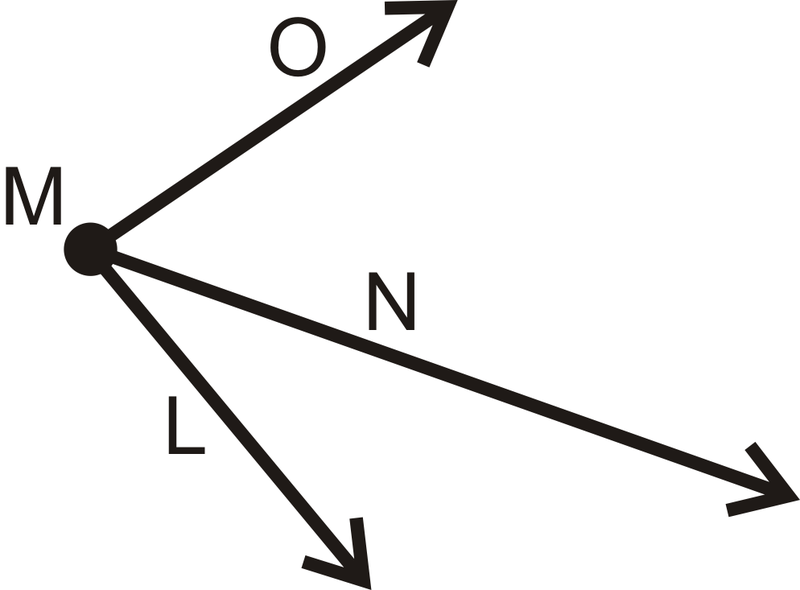Figure \(\PageIndex{15}\)2. If \(m \angle ABD = 100^{\circ}\), find \(x\).
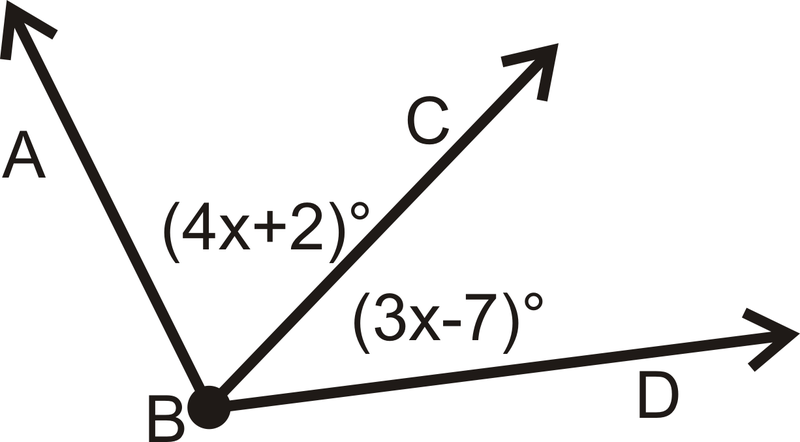Figure \(\PageIndex{16}\)For questions 3-6, determine if the statement is true or false.
- For an angle \(\angle ABC\),\(C\) is the vertex.
- For an angle \(\angle ABC\), \(\overline{AB}\) and \(\overline{BC}\) are the sides.
- The \(m\) in front of \(m \angle ABC\) means measure.
- The Angle Addition Postulate says that an angle is equal to the sum of the smaller angles around it.
For 7-12, draw the angle with the given degree, using a protractor and a ruler.
- \(55 ^{\circ}\)
- \(92 ^{\circ}\)
- \(178 ^{\circ}\)
- \(5 ^{\circ}\)
- \(120 ^{\circ}\)
- \(73 ^{\circ}\)
For 13-16, use a protractor to determine the measure of each angle.
-
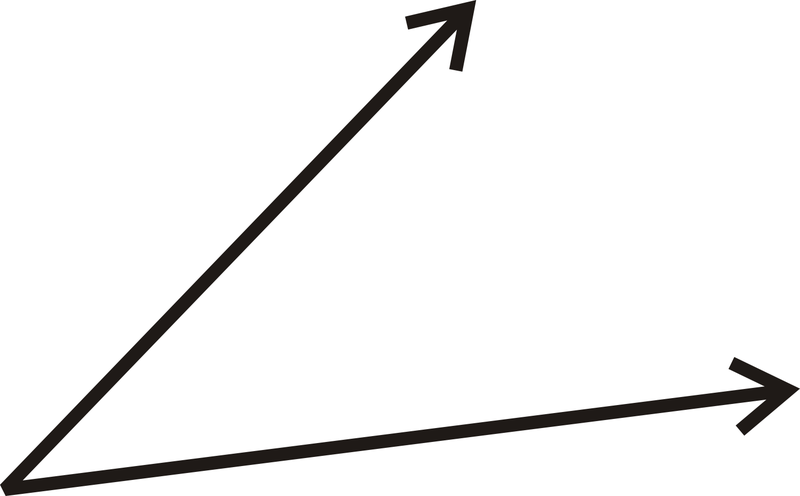Figure \(\PageIndex{17}\) -
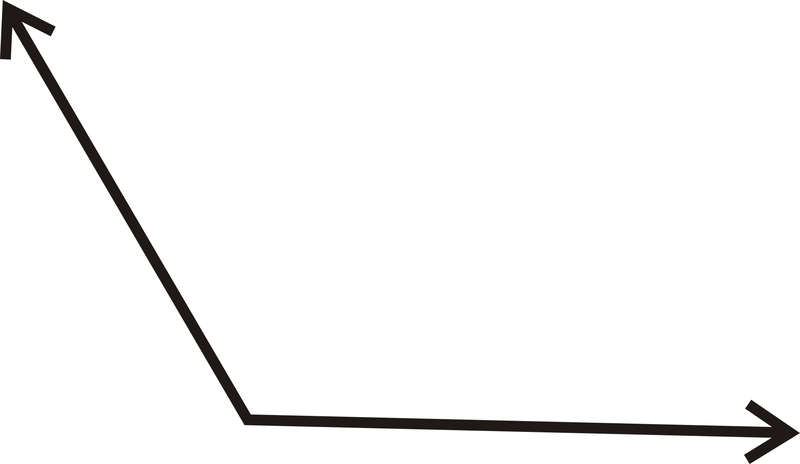Figure \(\PageIndex{18}\) -
Figure \(\PageIndex{19}\) -
Figure \(\PageIndex{20}\)
Solve for \(x\).
- \(m \angle ADC = 56^{\circ}\)
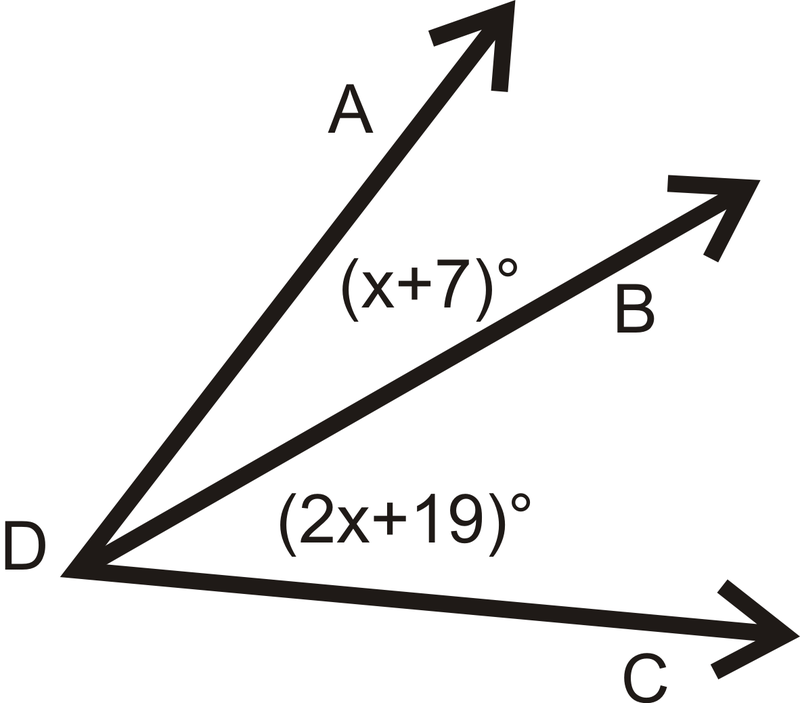Figure \(\PageIndex{21}\)Review (Answers)
To see the Review answers, open this PDF file and look for section 1.5.
Vocabulary
| Term | Definition |
|---|---|
| Angle | A geometric figure formed by two rays that connect at a single point or vertex. |
| Protractor | A protractor is a tool used to measure an angle in terms of degrees. |
| Vertex | A vertex is a point of intersection of the lines or rays that form an angle. |
Additional Resource
Interactive Element
Video: Angle Basics
Activities: Angle Measurement Discussion Questions
Study Aids: Angles Study Guide
Practice: Measuring Angles
Real World: Angle Measurement