1.8: Identificación de ángulos por vértice y rayo
- Page ID
- 107578
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Aprende a nombrar ángulos usando letras.
Figura\(\PageIndex{1}\)Donyell camina de su casa a su escuela. Después, después de la escuela camina a la casa de su amigo. Se da cuenta de que su viaje forma un ángulo. Decide nombrar el ángulo. Donyell califica su casa como punto\(H\), su escuela como punto S y la casa de su amigo como punto\(F\). ¿Se pueden utilizar los puntos para nombrar el ángulo formado por su viaje?
En este concepto, aprenderás sobre las partes de un ángulo.
Identificación de ángulos por vértice y rayo
Un ángulo es una de las figuras geométricas clave con las que trabajarás en geometría. Se crea un ángulo cuando dos rayos se conectan en un punto común.
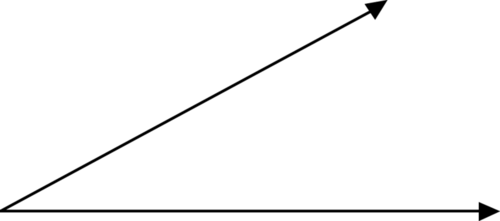Figura\(\PageIndex{2}\)Se puede ver que los dos rayos están conectados en un punto final común, llamado vértice. Esto forma el ángulo. Un ángulo es nombrado por puntos en los rayos.
Veamos un ejemplo de un ángulo.
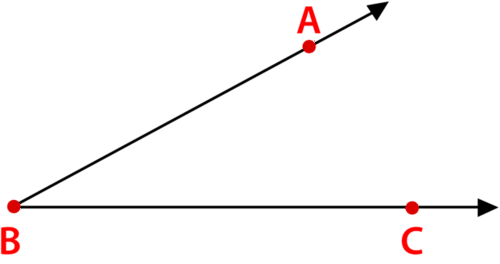Figura\(\PageIndex{3}\)Esto es ángulo\(ABC\). El vértice\(B\) está siempre en el medio. El símbolo para ángulo parece un ángulo pequeño.
\(\angle ABC\)
Ángulo\(ABC\) se nombra con este símbolo.
Ejemplo\(\PageIndex{1}\)
Antes, te dieron un problema sobre Donyell y su caminata a la escuela y luego a la casa de su amigo.
Nombra el ángulo si su casa es punto\(H\), su escuela es punto\(S\) y la casa de su amigo es punto\(F\).
Solución
Primero, determinar el punto final común.
\(S\)
Entonces, nombra el ángulo.
\(\angle HSF\)
La respuesta es\(\angle HSF\).
Ejemplo\(\PageIndex{2}\)
¿Cuál es el punto final común de los rayos que se forman\(\angle HIJ\)?
Solución
Primero, determinar el nombre del punto final común.
El vértice
A continuación, identifique la ubicación del vértice en el nombre del ángulo.
El punto medio
Entonces, escribe el punto.
\(I\)
La respuesta es\(I\). El punto final común de los rayos que\(\angle HIJ\) se forman es\(I\).
Ejemplo\(\PageIndex{3}\)
Nombra este ángulo. Asegúrate de que el vértice esté en el medio.
Figura\(\PageIndex{4}\)Solución
Primero, localice el punto final común.
\(E\)
Entonces, nombra el ángulo.
\(\angle DEF\)
La respuesta es \(\angle DEF\).
Ejemplo\(\PageIndex{4}\)
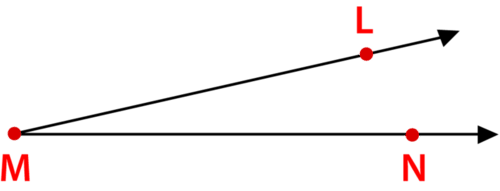Figura\(\PageIndex{5}\)Solución
Primero, localice el punto final común.
\(M\)
Entonces, nombra el ángulo.
\(\angle LMN\)
La respuesta es\(\angle LMN\)
Ejemplo\(\PageIndex{5}\)
¿Cuál es el punto final común de los rayos que se forman\(\angle QRS\)?
Solución
Primero, determinar el nombre del punto final común.
El vértice
A continuación, identifique la ubicación del vértice en el nombre del ángulo.
El punto medio
Entonces, escribe el punto.
\(R\)
La respuesta es\(R\). El punto final común de los rayos que\(\angle QRS\) se forman es\(R\).
Revisar
Dibuja un cuadro para ilustrar cada una de las figuras geométricas nombradas.
- \(\overrightarrow{AB}\)
- \(\overleftrightarrow{CD}\)
- \(\overleftrightarrow{DE}\)
- \(\angle ABC\)
- \(\angle LMN\)
- \(\overline{XY}\)
- \(\overrightarrow{PQ}\)
- \(\overleftrightarrow{GH}\)
- \(\overleftrightarrow{AB} \parallel \overleftrightarrow{DE}\)
- \(\overleftrightarrow{LM} \parallel \overleftrightarrow{DE}\)
- \(\overleftrightarrow{RS} \parallel \overleftrightarrow{TU}\)
- \(\overline{DF} \parallel \overline{XY}\)
Defina los siguientes términos.
- Ray
- Línea
- Vértice
- Segmento de Línea
Reseña (Respuestas)
Para ver las respuestas de Revisar, abra este archivo PDF y busque la sección 9.3.
El vocabulario
| Término | Definición |
|---|---|
| Ángulo | Una figura geométrica formada por dos rayos que conectan en un solo punto o vértice. |
| Líneas de intersección | Las líneas que se cruzan son líneas que se cruzan o se encuentran en algún momento. |
| línea | Una línea es una figura recta unidimensional que se extiende para siempre en direcciones opuestas. |
| segmento de línea | Un segmento de línea es una parte de una línea que tiene dos puntos finales. |
| Paralelo | Dos o más líneas son paralelas cuando se encuentran en el mismo plano y nunca se cruzan. Estas líneas siempre tendrán la misma pendiente. |
| Punto | Un punto es una ubicación en el espacio que no tiene tamaño ni forma. |
| Punto de intersección | Un punto de intersección es el punto en el que se encuentran dos líneas que se cruzan. |
| Ray | Un rayo es una parte de una línea que tiene un punto final y continúa indefinidamente en una dirección. |
| Vértice | Un vértice es un punto de intersección de las líneas o rayos que forman un ángulo. |
Recurso Adicional
Elemento Interactivo
Video: Introducción a los ángulos
Práctica: Identificación de ángulos por vértice y rayo