4.17: Teorema de la suma del ángulo del triángulo
- Page ID
- 107497
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Los ángulos interiores de un triángulo se suman a 180 grados Usa ecuaciones para encontrar medidas de ángulo faltantes dada la suma de 180 grados.
Teorema de suma de triángulo
El Teorema de la Suma del Triángulo dice que los tres ángulos interiores de cualquier triángulo suman\(180^{\circ}\).
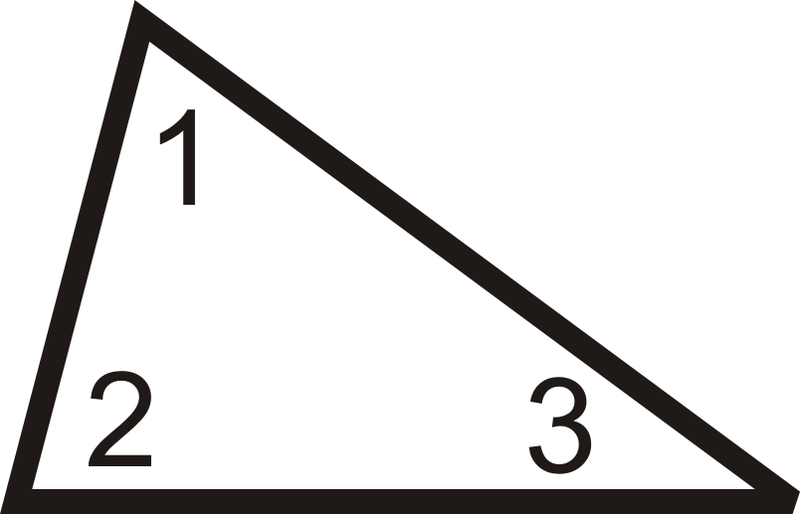
\(m\angle 1+m\angle 2+m\angle 3=180^{\circ}\).
Aquí hay una prueba del Teorema de la Suma del Triángulo.
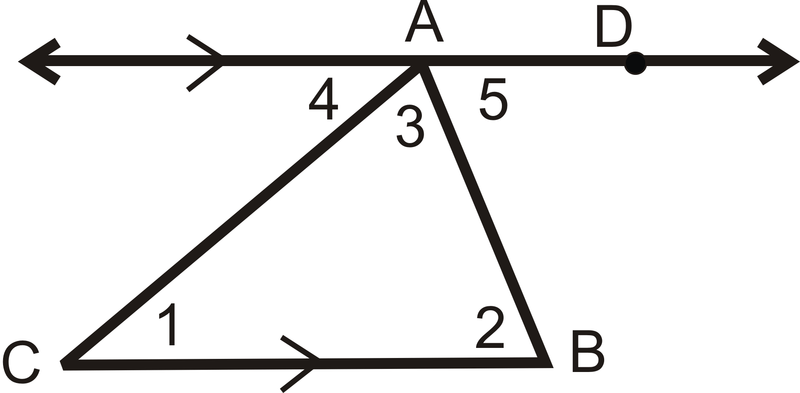
Dado:\(\Delta ABC\) con\(\overleftrightarrow{AD} \parallel \overline{BC}\)
Demostrar:\(m\angle 1+m\angle 2+m\angle 3=180^{\circ}\)
| Comunicado | Razón |
|---|---|
| 1. \(\Delta ABC with \overleftrightarrow{AD} \parallel \overline{BC}\) | Dado |
| 2. \\(angle 1\cong \angle 4,\: \angle 2\cong \angle 5\) | Teorema de ángulos interiores alternos |
| 3. \(m\angle 1=m\angle 4,\: m\angle 2=m\angle 5\) | \ cong ángulos tienen = medidas |
| 4. \(m\angle 4+m\angle CAD=180^{\circ}\) | Postulado de Par Lineal |
| 5. \(m\angle 3+m\angle 5=m\angle CAD\) | Postulado de Adición de Ángulo |
| 6. \(m\angle 4+m\angle 3+m\angle 5=180^{\circ}\) | Sustitución PoE |
| 7. \(m\angle 1+m\angle 3+m\angle 2=180^{\circ}\) | Sustitución PoE |
Puedes usar el Teorema de la suma de triángulos para encontrar los ángulos faltantes en los triángulos.
¿Y si supieras que dos de los ángulos en un triángulo medían\(55^{\circ}\)? ¿Cómo se pudo encontrar la medida del tercer ángulo?
Ejemplo\(\PageIndex{1}\)
Dos ángulos interiores de un triángulo miden\(50^{\circ}\) y\(70^{\circ}\). ¿Cuál es el tercer ángulo interior del triángulo?
Solución
\(50^{\circ}+70^{\circ}+x=180^{\circ}\).
Resuelve esta ecuación y encuentras que el tercer ángulo es\(60^{\circ}\).
Ejemplo\(\PageIndex{2}\)
Encuentra el valor de\(x\) y la medida de cada ángulo.
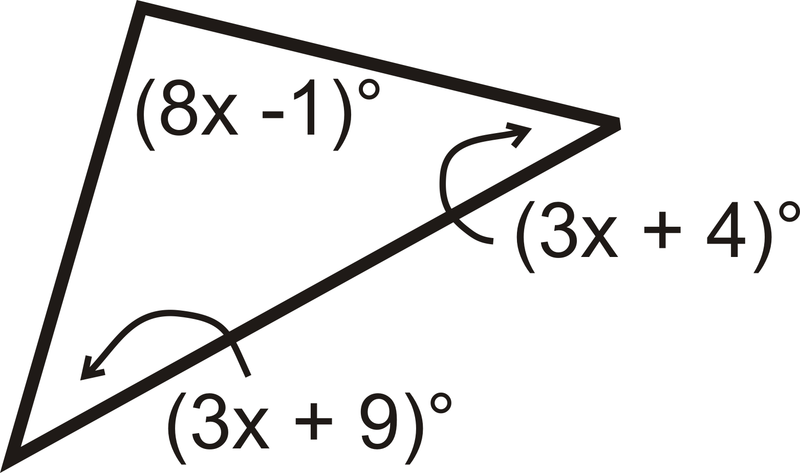
Solución
Todos los ángulos se suman a\(180^{\circ}\).
\(\begin{align*} (8x−1)^{\circ}+(3x+9)^{\circ}+(3x+4)^{\circ}&=180^{\circ} \\ (14x+12)^{\circ}&=180^{\circ} \\ 14x&=168 \\ x&=12\end{align*} \)
Sustituye en 12\(x\) para encontrar cada ángulo.
\([3(12)+9]^{\circ}=45^{\circ} \qquad [3(12)+4]^{\circ}=40^{\circ} \qquad [8(12)−1]^{\circ}=95^{\circ}\)
Ejemplo\(\PageIndex{3}\)
¿Qué es m\ ángulo T?
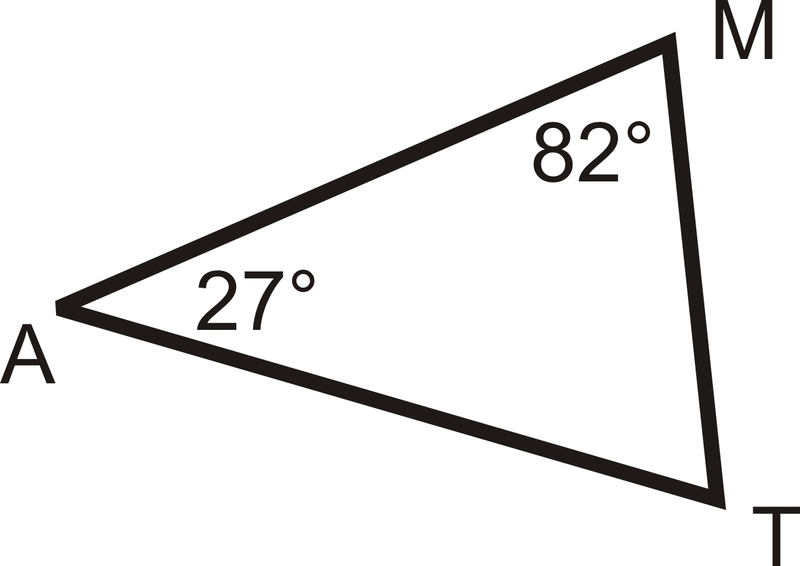
Solución
Sabemos que los tres ángulos en el triángulo deben sumar\(180^{\circ}\). Para resolver este problema, establezca una ecuación y sustituya en la información que conozca.
\(\begin{align*} m\angle M+m\angle A+m\angle T&=180^{\circ} \\ 82^{\circ}+27^{\circ}+m\angle T&=180^{\circ} \\ 109^{\circ}+m\angle T&=180^{\circ} \\ m\angle T &=71^{\circ}\end{align*}\)
Ejemplo\(\PageIndex{4}\)
¿Cuál es la medida de cada ángulo en un triángulo equiangular?
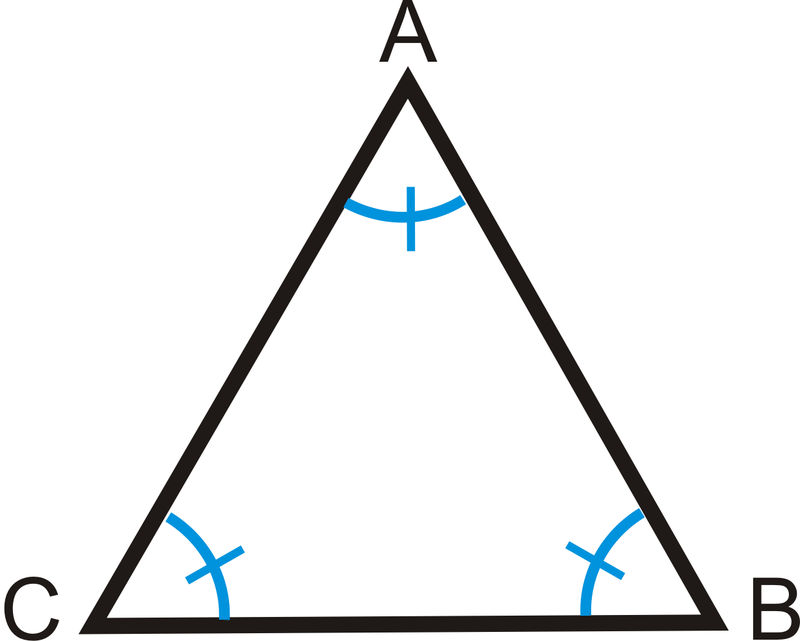
Solución
Para resolver, recuerda que\(\Delta ABC\) es un triángulo equiangular, por lo que los tres ángulos son iguales. Escribe una ecuación.
\(\begin{align*} m\angle A+m\angle B+m\angle C &=180^{\circ} \\ m\angle A+m\angle A+m\angle A&=180^{\circ} \qquad &Substitute,\: all\: angles\: are \: equal. \\ 3m\angle A&=180^{\circ} \qquad &Combine\:like \:terms. \\ m\angle A&=60^{\circ}\end{align*}\)
Si\(m\angle A=60^{\circ}\), entonces\(m\angle B=60^{\circ}\) y\(m\angle C=60^{\circ}\).
Cada ángulo en un triángulo equiangular es\(60^{\circ}\).
Ejemplo\(\PageIndex{5}\)
Encuentra la medida del ángulo faltante.
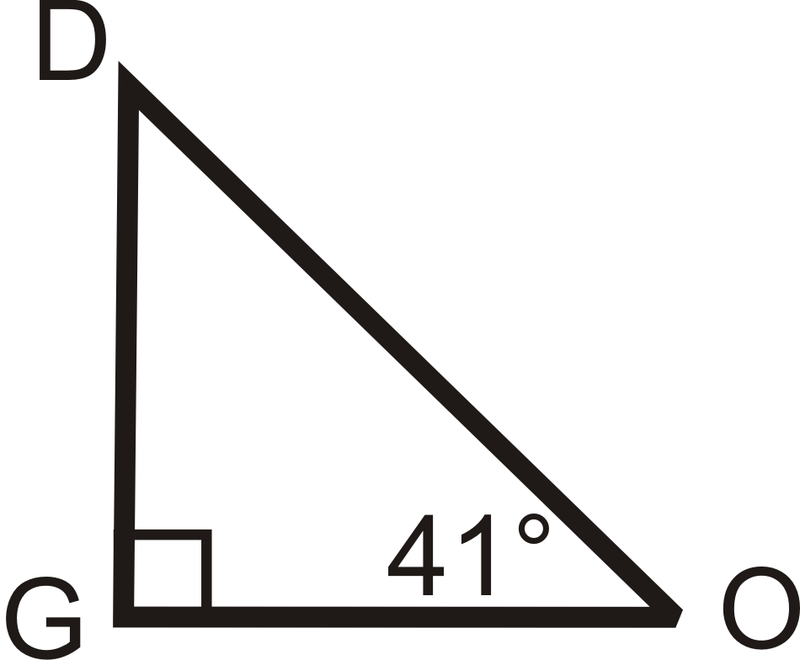
Solución
Eso lo sabemos\(m\angle O=41^{\circ}\) y\(m\angle G=90^{\circ}\) porque es un ángulo recto. Establezca una ecuación como en el Ejemplo 3.
\(\begin{align*} m\angle D+m\angle O+m\angle G&=180^{\circ} \\ m\angle D+41^{\circ}+90^{\circ}&=180^{\circ} \\ m\angle D+41^{\circ}&=90^{\circ}\\ m\angle D=49^{\circ}\end{align*}\)
Revisar
Determinar\(m\angle 1\) en cada triángulo.
1.
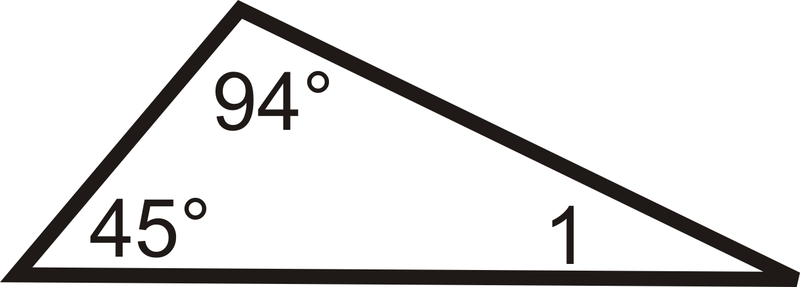
2.
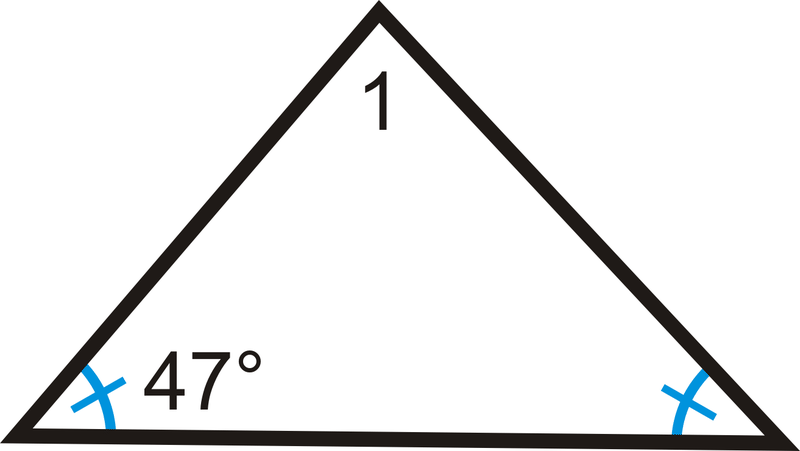
3.
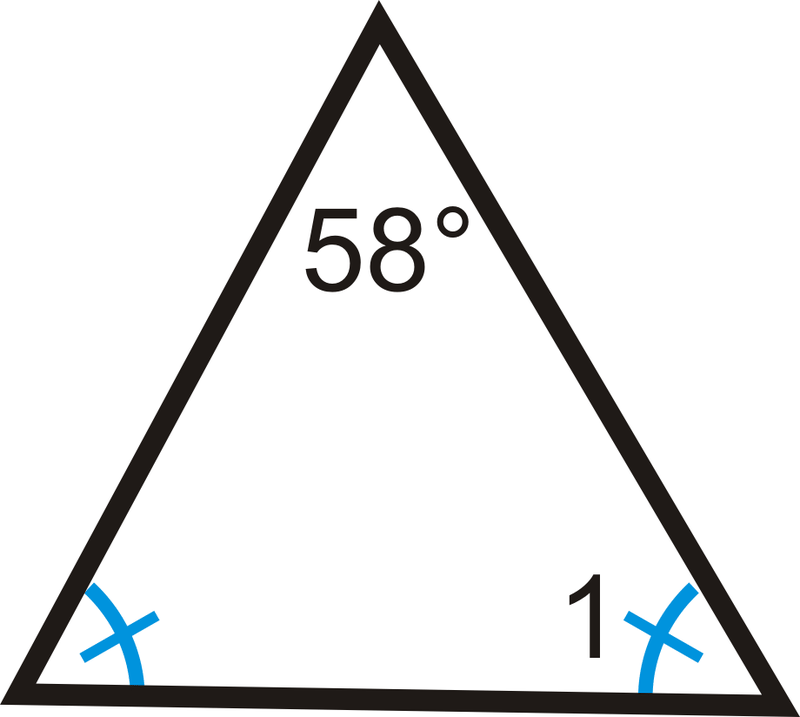
4.
5.
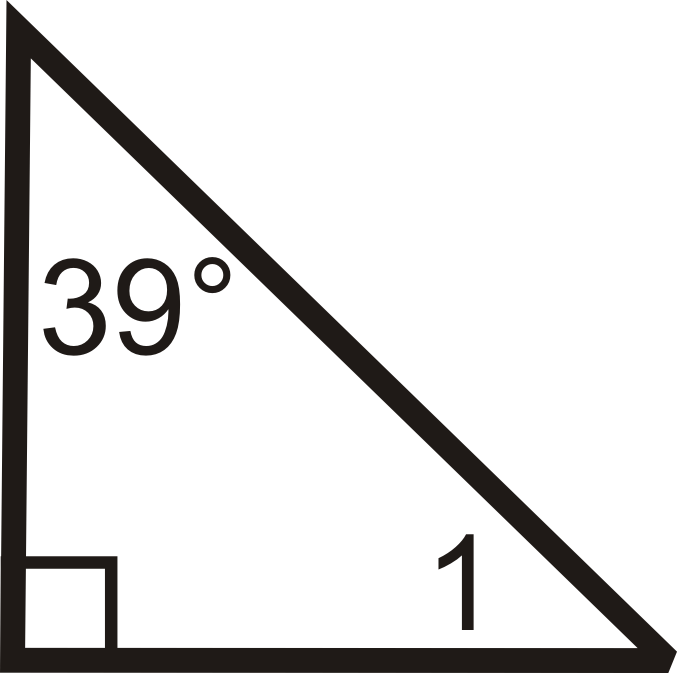
6.
7.
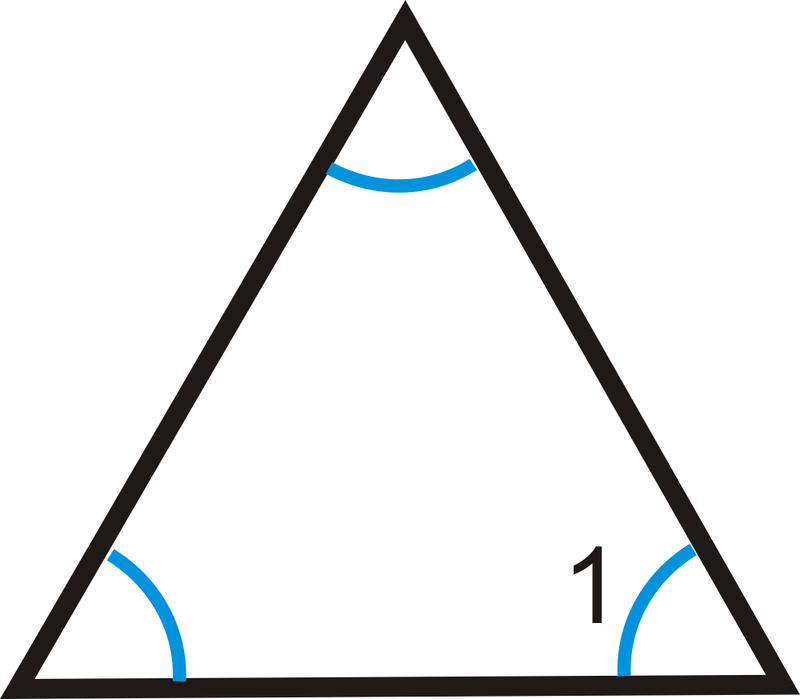
8. Dos ángulos interiores de un triángulo miden\(32^{\circ}\) y\(64^{\circ}\). ¿Cuál es el tercer ángulo interior del triángulo?
9. Dos ángulos interiores de un triángulo miden\(111^{\circ}\) y\(12^{\circ}\). ¿Cuál es el tercer ángulo interior del triángulo?
10. Dos ángulos interiores de un triángulo miden\(2^{\circ}\) y\(157^{\circ}\). ¿Cuál es el tercer ángulo interior del triángulo?
Encuentra el valor de\(x\) y la medida de cada ángulo.
11.
12.
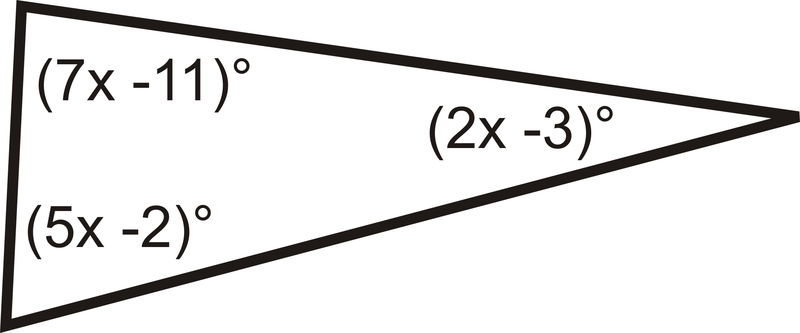
13.
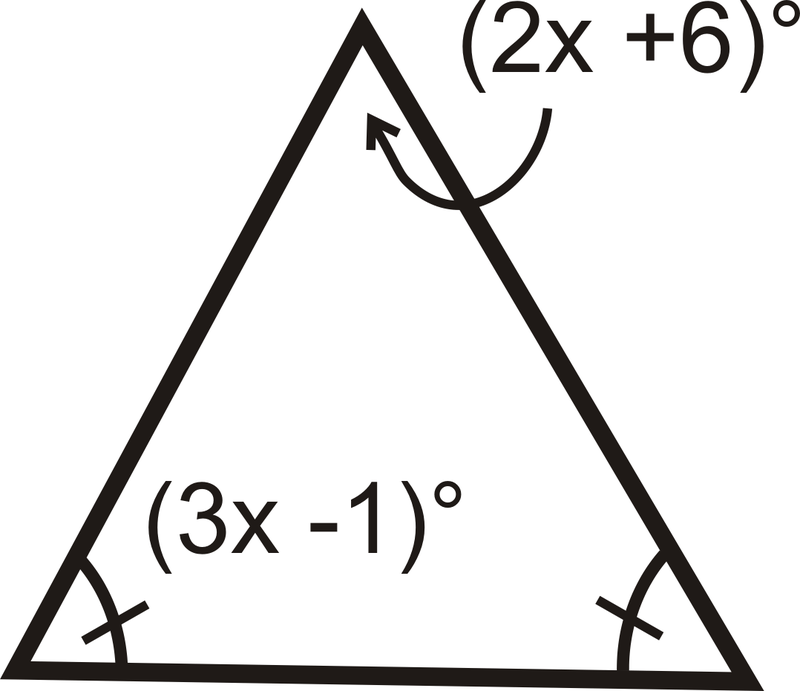
14.
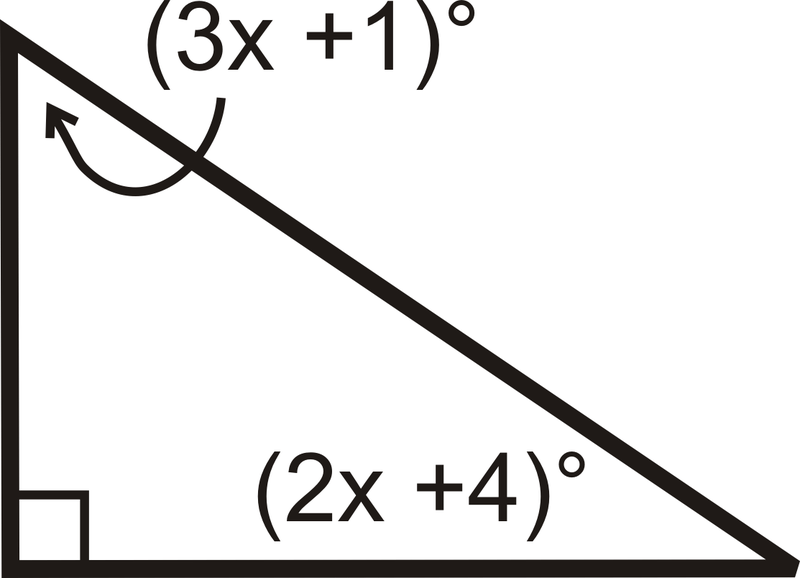
15.
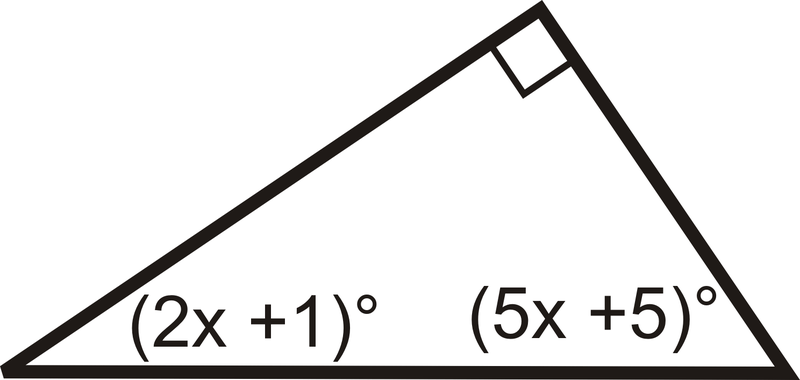
Reseña (Respuestas)
Para ver las respuestas de Revisar, abra este archivo PDF y busque la sección 4.1.
Recursos
El vocabulario
| Término | Definición |
|---|---|
| Teorema de suma de triángulo | El Teorema de la Suma del Triángulo establece que los tres ángulos interiores de cualquier triángulo suman 180 grados. |
Recursos adicionales
Elemento Interactivo
Video: Principios del teorema de la suma del triángulo - Básico
Actividades: Teorema de la suma del triángulo Preguntas de discusión
Ayudas de estudio: Guía de estudio de las relaciones
Práctica: Teorema de suma de ángulos triangulares
Mundo real: Teorema de la suma del triángulo