4.18: Ángulos y teoremas exteriores
- Page ID
- 107494
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Los ángulos exteriores son iguales a la suma de los interiores remotos.
Ángulos exteriores
Un Ángulo Exterior es el ángulo formado por un lado de un polígono y la extensión del lado adyacente.
En todos los polígonos, hay dos conjuntos de ángulos exteriores, uno que gira alrededor de las agujas del reloj y el otro va en sentido antihorario.
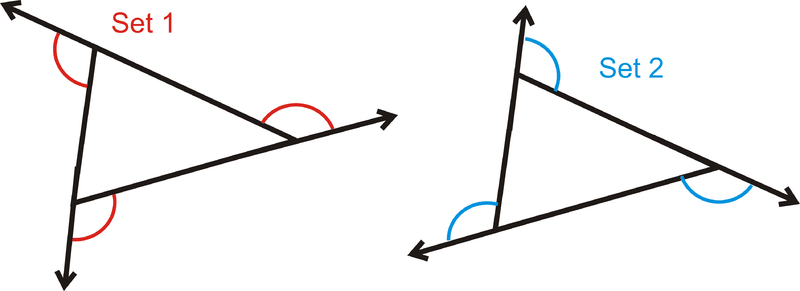
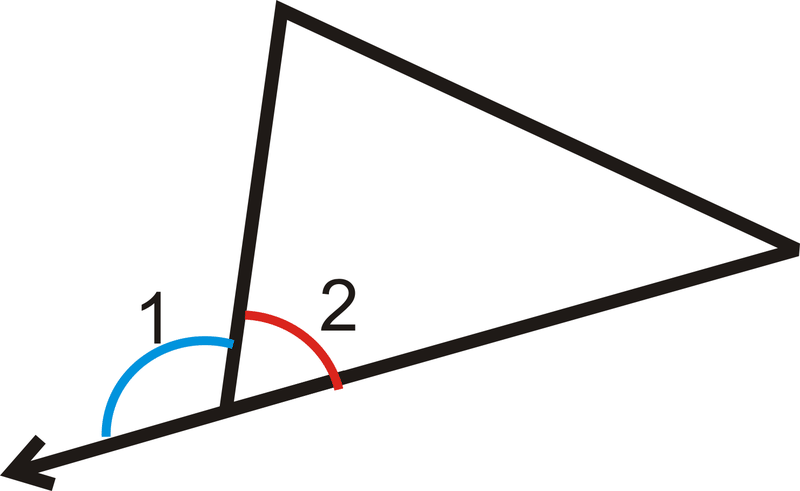
Observe que el ángulo interior y su ángulo exterior adyacente forman un par lineal y se suman a\(180^{\circ}\).
\(m\angle 1+m\angle 2=180^{\circ} \)
Hay dos teoremas importantes a conocer que involucran ángulos exteriores: el Teorema de la Suma de Ángulo Exterior y el Teorema de Ángulo Exterior.
El teorema de la suma de ángulos exteriores establece que los ángulos exteriores de cualquier polígono siempre se sumarán\(360^{\circ}\).
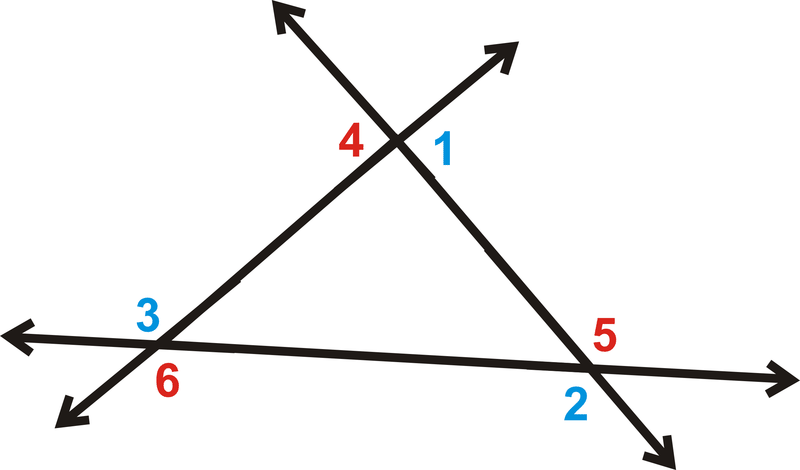
\(m\angle 1+m\angle 2+m\angle 3=360^{\circ}\)
\(m\angle 4+m\angle 5+m\angle 6=360^{\circ}\).
El Teorema del Ángulo Exterior establece que un ángulo exterior de un triángulo es igual a la suma de sus ángulos interiores remotos. (Los ángulos interiores remotos son los dos ángulos interiores en un triángulo que no son adyacentes al ángulo exterior indicado).
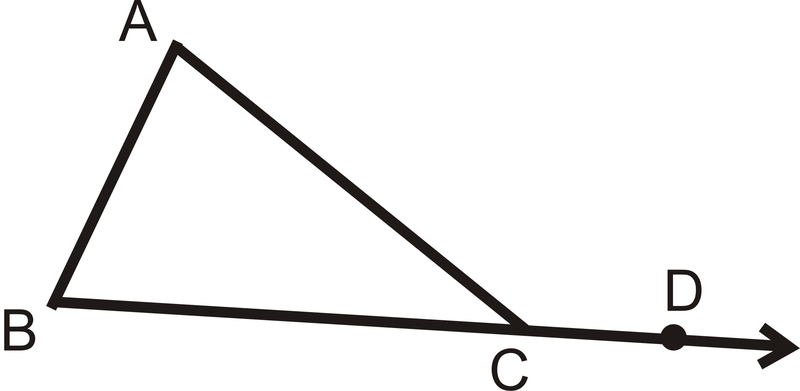Figura\(\PageIndex{4}\)\(m\angle A+m\angle B=m\angle ACD\)
¿Y si supieras que dos de los ángulos exteriores de un triángulo medían\(130^{\circ}\)? ¿Cómo pudo encontrar la medida del tercer ángulo exterior?
Ejemplo\(\PageIndex{1}\)
Dos ángulos interiores de un triángulo son\(40^{\circ}\) y\(73^{\circ}\). ¿Cuáles son las medidas de los tres ángulos exteriores del triángulo?
Solución
Recuerde que cada ángulo interior forma un par lineal (suma\(180^{\circ}\)) con un ángulo exterior. Entonces, ya que uno de los ángulos interiores es\(40^{\circ}\) eso significa que uno de los ángulos exteriores es\(140^{\circ}\) (porque\(40+140=180\)). De igual manera, dado que otro de los ángulos interiores es\(73^{\circ}\), uno de los ángulos exteriores debe serlo\(107^{\circ}\). El tercer ángulo interior no se nos da, pero podríamos averiguarlo usando el Teorema de la Suma del Triángulo. También podemos utilizar el Teorema de la Suma de Ángulo Exterior. Si dos de los ángulos exteriores son\(140^{\circ}\) y\(107^{\circ}\), entonces el tercer Ángulo Exterior debe ser\(113^{\circ}\) desde\(140+107+113=360\).
Entonces, las medidas de los tres ángulos exteriores son 140, 107 y 113.
Ejemplo\(\PageIndex{2}\)
Encuentra el valor\(x\) y la medida de cada ángulo.
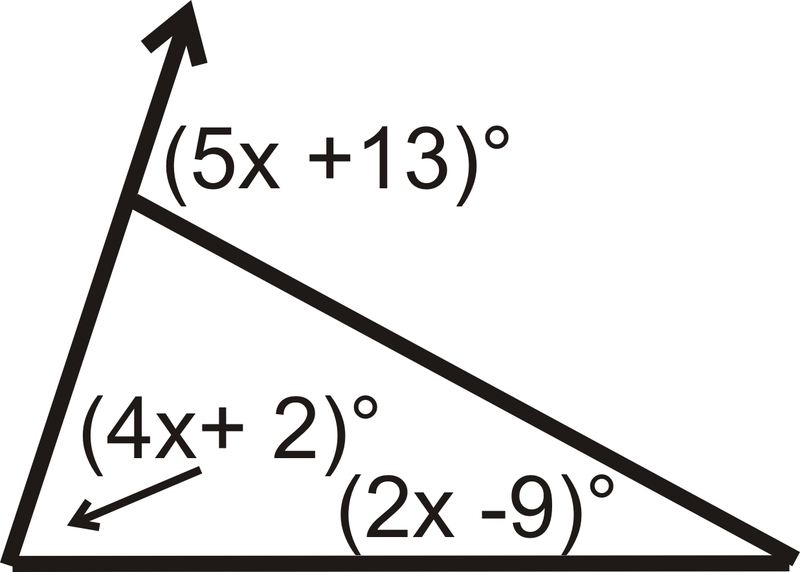
Solución
Configura una ecuación usando el Teorema del Ángulo Exterior.
\(\begin{align*} \underbrace{(4x+2)^{\circ}+(2x−9)^{\circ}}_\text{remote interior angles}&=\underbrace{(5x+13)^{\circ}}_\text{exterior angle} \\ (6x−7)^{\circ}&=(5x+13)^{\circ} \\ x&=20 \end{align*}\)
Sustituye en 20\(x\) para encontrar cada ángulo.
\([4(20)+2]^{\circ}=82^{\circ}[2(20)−9]^{\circ}=31^{\circ} \qquad Exterior \:angle:\: [5(20)+13]^{\circ}=113^{\circ}\)
Ejemplo\(\PageIndex{3}\)
Encuentra la medida de\(\angle RQS\).
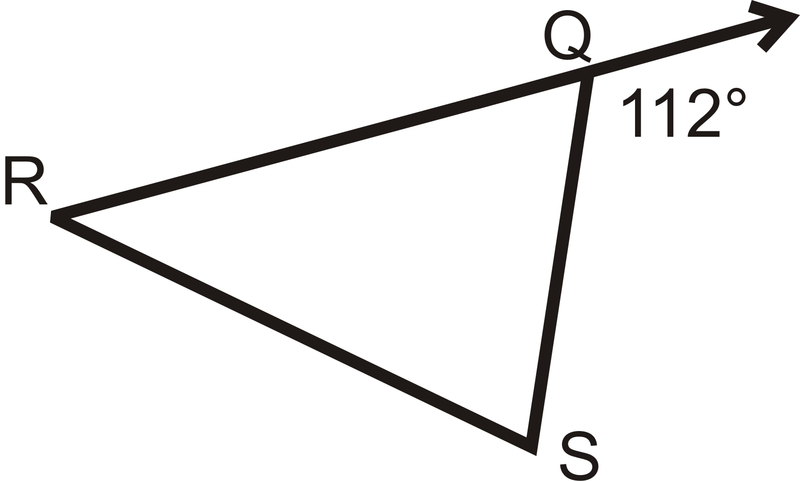Figura\(\PageIndex{5}\)Solución
Observe que\(112^{\circ}\) es un ángulo exterior de\(\Delta RQS\) y es complementario a\(\angle RQS\).
Configure una ecuación para resolver el ángulo faltante.
\(\begin{align*}112^{\circ}+m\angle RQS &=180^{\circ} \\ m\angle RQS&=68^{\circ}\end{align*}\)
Ejemplo\(\PageIndex{4}\)
Encuentra las medidas de los ángulos numerados interior y exterior en el triángulo.
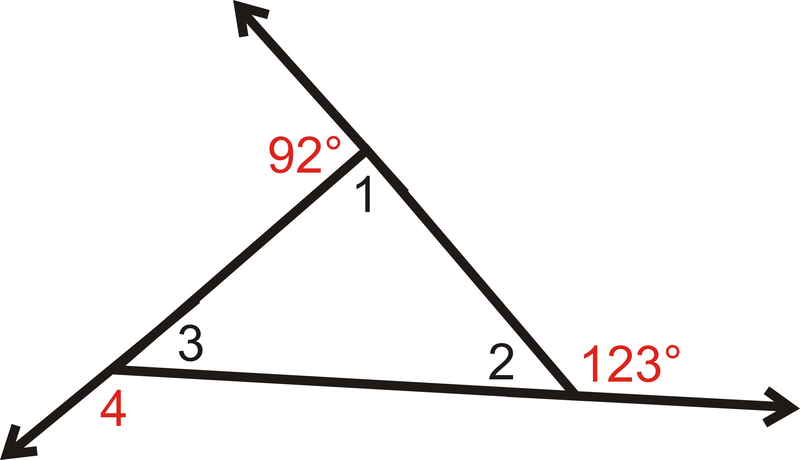Figura\(\PageIndex{6}\)Solución
Eso lo sabemos\(m\angle 1+92^{\circ}=180^{\circ}\) porque forman un par lineal. Entonces, m\ ángulo 1=88^ {\ circ}\).
Del mismo modo,\(m\angle 2+123^{\circ}=180^{\circ}\) porque forman un par lineal. Entonces, m\ ángulo 2=57^ {\ circ}\).
También sabemos que los tres ángulos interiores deben sumar 180^ {\ circ}\) por el Teorema de la Suma del Triángulo.
\(\begin{align*} m\angle 1+m\angle 2+m\angle 3&=180^{\circ} \qquad by\: the \:Triangle \:Sum \:Theorem. \\ 88^{\circ}+57^{\circ}+m\angle 3&=180 \\ m\angle 3&=35^{\circ}\end{align*}\)
Por último,\(m\angle 3+m\angle 4=180^{\circ} \qquad because\: they\: form \:a \:linear \:pair.\)
\(\begin{align*} 35^{\circ}+m\angle 4&=180^{\circ} \\ m\angle 4&=145^{\circ}\end{align*}\)
Ejemplo\(\PageIndex{5}\)
¿Cuál es el valor de\(p\) en el triángulo de abajo?
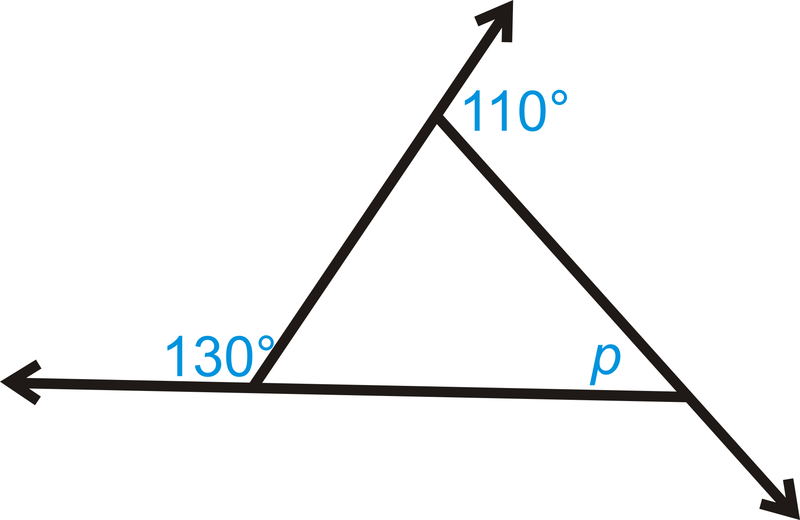
Solución
Primero, necesitamos encontrar el ángulo exterior faltante, al que llamaremos\(x\). Configure una ecuación usando el Teorema de la Suma de Ángulo Exterior.
\(\begin{align*} 130^{\circ}+110^{\circ}+x&=360^{\circ} \\ x&=360^{\circ}−130^{\circ}−110^{\circ} \\ x&=120^{\circ}\end{align*} \)
\(x\)y\(p\) sumar\(180^{\circ}\) porque son un par lineal.
\(\begin{align*} x+p&=180^{\circ} \\ 120^{\circ}+p&=180^{\circ} \\ p&=60^{\circ}\end{align*}\)
Revisar
Determinar\(m\angle 1\).
-
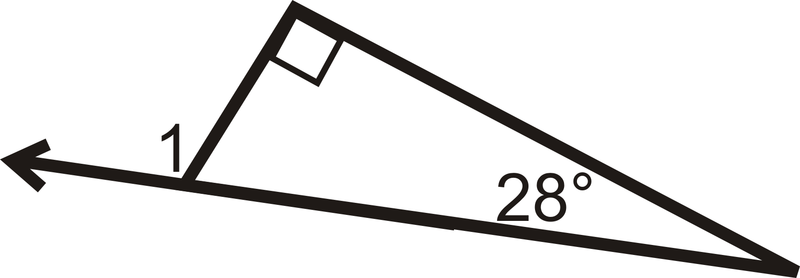
Figura\(\PageIndex{8}\) -
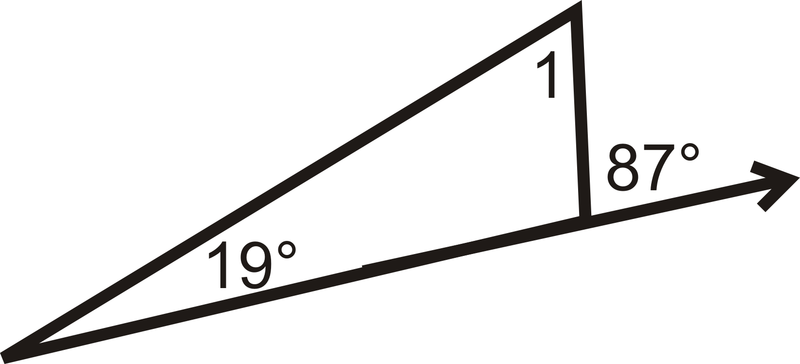
Figura\(\PageIndex{9}\) -
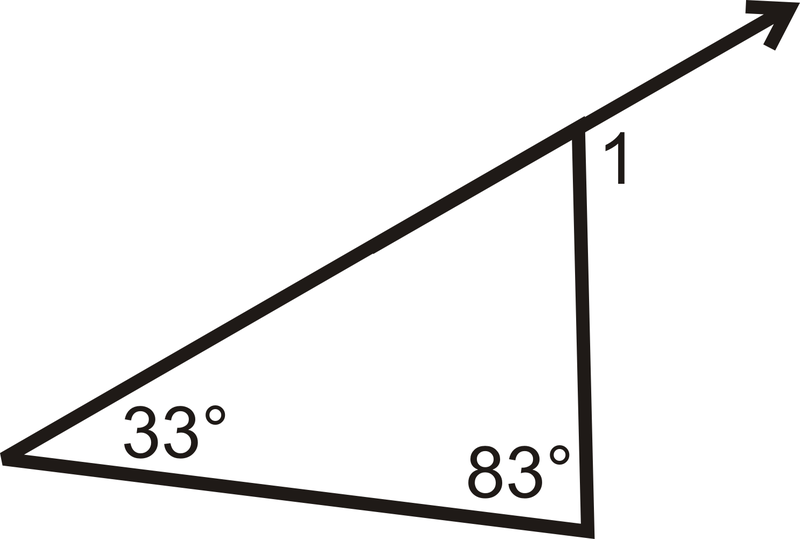
Figura\(\PageIndex{10}\) -
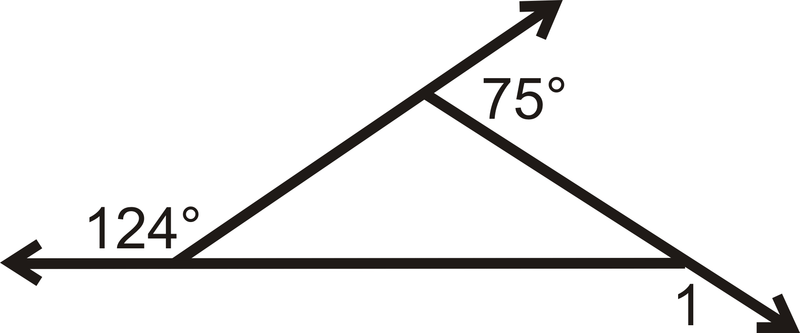
Figura\(\PageIndex{11}\) -
Figura\(\PageIndex{12}\) -
Figura\(\PageIndex{13}\)
Utilice la siguiente imagen para los siguientes tres problemas:
- ¿Qué es\(m\angle 1+m\angle 2+m\angle 3\)?
- ¿Qué es\(m\angle 4+m\angle 5+m\angle 6\)?
- ¿Qué es\(m\angle 7+m\angle 8+m\angle 9\)?
Resolver para\(x\).
-
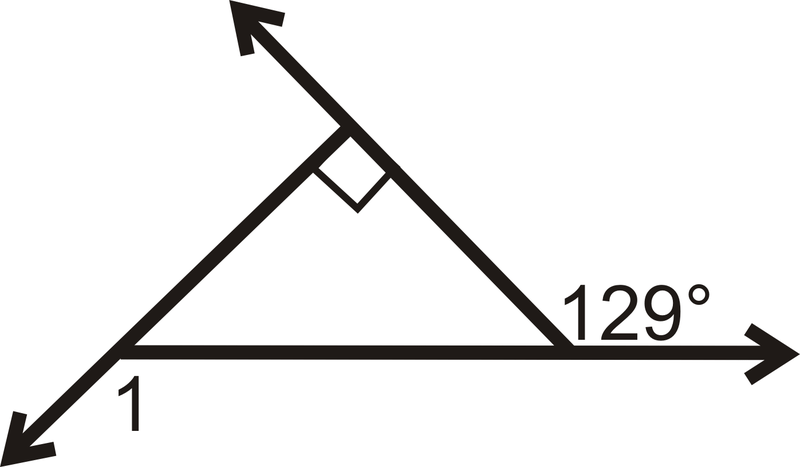
Figura\(\PageIndex{14}\) -
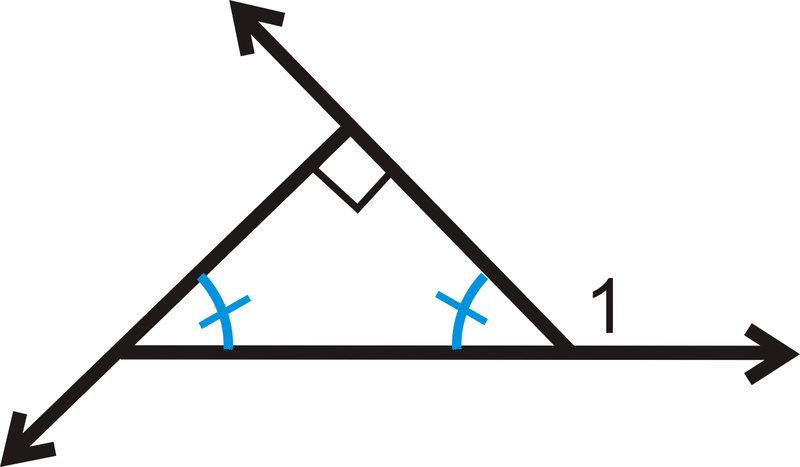
Figura\(\PageIndex{15}\) -
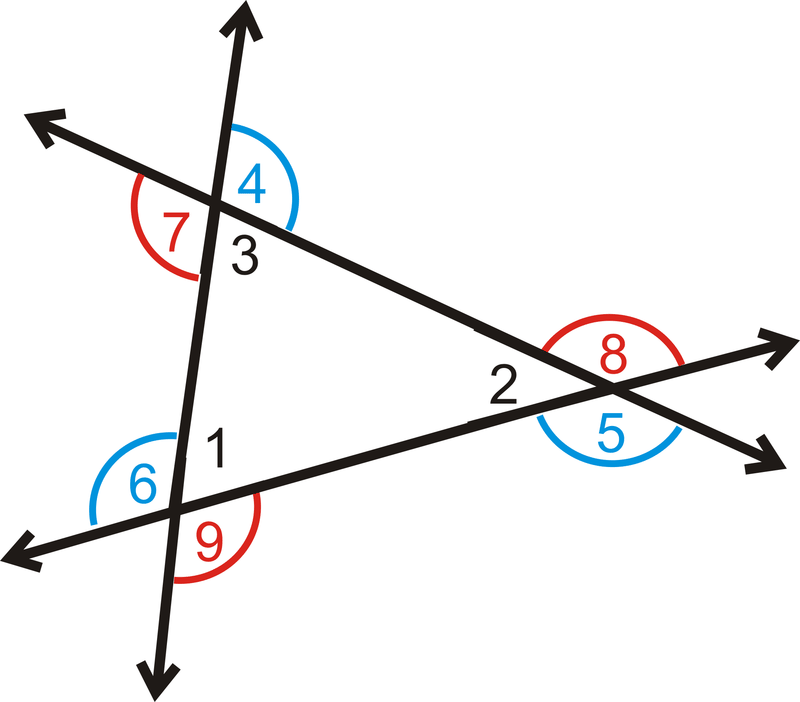
Figura\(\PageIndex{16}\)
Recursos
vocabulario
| Término | Definición |
|---|---|
| Ángulos exteriores | Un ángulo exterior es el ángulo formado por un lado de un polígono y la extensión del lado adyacente. |
| ángulos interiores | Los ángulos en el interior de un polígono. |
| ángulos interiores remotos | Los ángulos interiores remotos (de un triángulo) son los dos ángulos interiores que no son adyacentes al ángulo exterior indicado. |
| Teorema de suma de triángulo | El Teorema de la Suma del Triángulo establece que los tres ángulos interiores de cualquier triángulo siempre se sumarán\(180^{\circ}\). |
| Teorema de la suma de ángulos exteriores | El teorema de la suma de ángulos exteriores establece que los ángulos exteriores de cualquier polígono siempre sumarán 360 grados. |
Recursos adicionales
Elemento interactivo
Video: Ejemplos de Teoremas de Ángulos Exteriores - Básico
Actividades: Teoremas de ángulos exteriores Preguntas de discusión
Ayudas de estudio: Guía de estudio de las relaciones
Práctica: Ángulos y teoremas exteriores
Mundo real: Teorema de ángulos exteriores