4.16: HL
- Page ID
- 107476
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\(\newcommand{\longvect}{\overrightarrow}\)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Congruencia Triángulo HL
Teorema de congruencia de hipotenuso-pierna
Si la hipotenusa y la pierna en un triángulo rectángulo son congruentes con la hipotenusa y la pierna en otro triángulo rectángulo, entonces los dos triángulos son congruentes. Esto se llama Teorema de Congruencia Hipotenusa-Pierna (HL). Tenga en cuenta que solo funcionará para triángulos rectos.
Si\(\Delta ABC\) y\(\Delta XYZ\) son ambos triángulos rectos y\(\overline{AB}\cong \overline{XY}\) y\(\overline{BC}\cong \overline{YZ}\) entonces\(\Delta ABC\cong \Delta XYZ\).
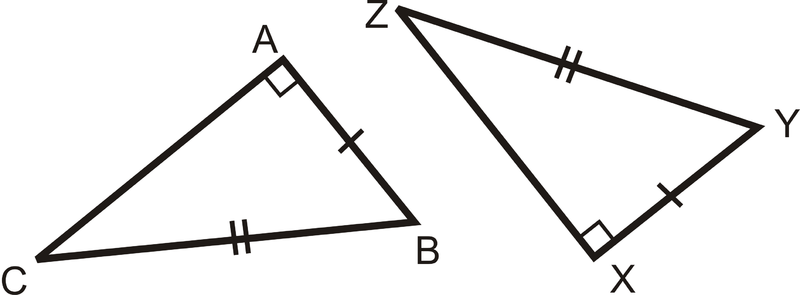
¿Y si te dieran dos triángulos rectos y te proporcionaran solo la medida de sus hipotenusas y una de sus piernas? ¿Cómo podrías determinar si los dos triángulos rectos eran congruentes?
Ejemplo\(\PageIndex{1}\)
Rellene los espacios en blanco en el comprobante a continuación.
Dado:
\(\overline{SV}\perp \overline{WU}\)
\(T\)es el punto medio de\(\overline{SV}\) y\(\overline{WU}\)
Demostrar:\(\overline{WS}\cong \overline{UV}\)
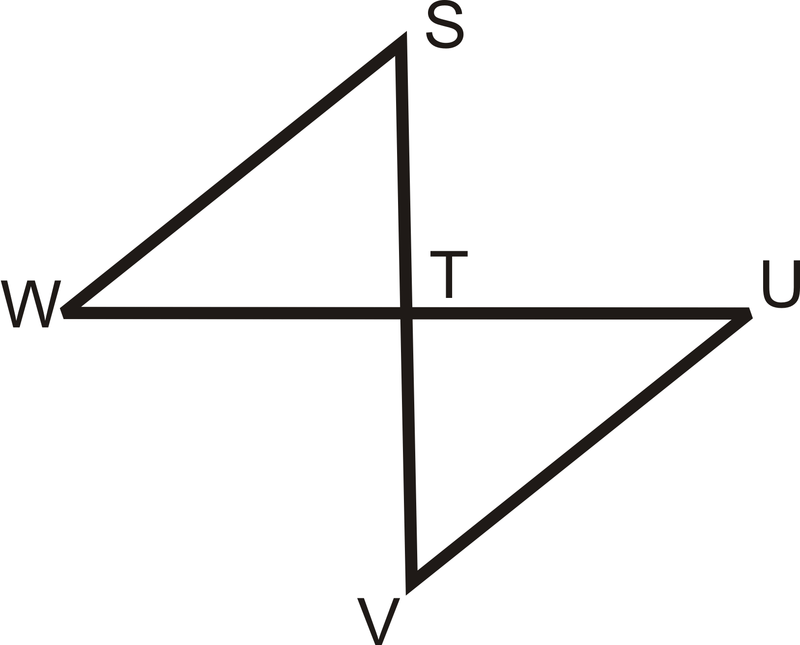
Solución
| Declaración | Razón |
|---|---|
| 1. | 1. |
| 2. \(\angle STW\)y\(\angle UTV\) son ángulos rectos | 2. |
| 3. | 3. |
| 4. \(\overline{ST}\cong \overline{TV}\),\(\overline{WT}\cong \overline{TU}\) | 4. |
| 5. \(\Delta STW\cong \Delta UTV\) | 5. |
| 6. \(\overline{WS}\cong \overline{UV}\) | 6. |
| Declaración | Razón |
|---|---|
| 1. \(\overline{SV}\perp \overline{WU}\) | 1. Dado |
| 2. \(\angle STW\)y\(\angle UTV\) son ángulos rectos | 2. Definición de líneas perpendiculares. |
| 3. \(T\)es el punto medio de\(\overline{SV}\) y\(\overline{WU}\) | 3. Dado |
| 4. \(\overline{ST}\cong \overline{TV}\),\(\overline{WT}\cong \overline{TU}\) | 4. Definición de punto medio |
| 5. \(\Delta STW\cong \Delta UTV\) | 5. SAS |
| 6. \(\overline{WS}\cong \overline{UV}\) | 6. CPCTC |
Tenga en cuenta que a pesar de que estos eran triángulos rectos, no usamos el atajo de congruencia HL porque originalmente no se nos dio que las dos hipotenusas fueran congruentes. El atajo de congruencia SAS fue más rápido en este caso.
Ejemplo\(\PageIndex{2}\)
Explique por qué funciona el atajo Congruencia HL.
El Teorema de Pitágoras, que dice, para cualquier triángulo rectángulo, esta ecuación es cierta:
\((leg)^2+(leg)^2=(hypotenuse)^2\)
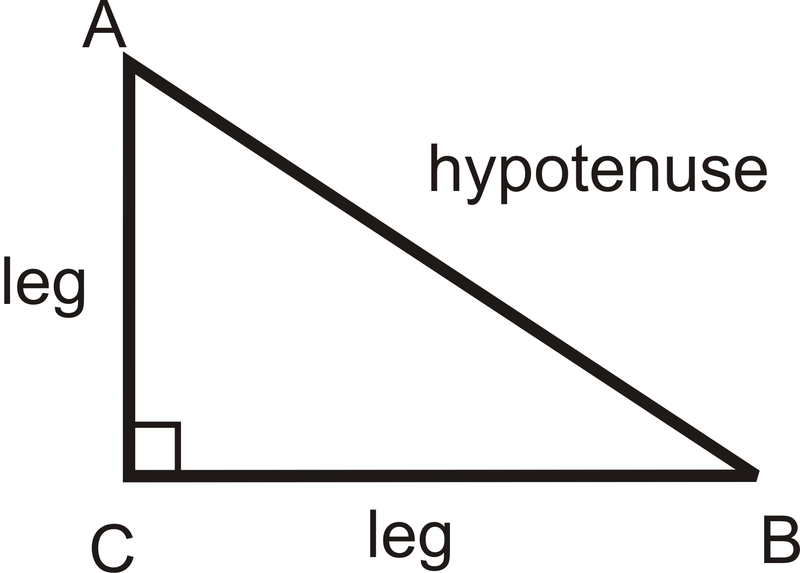
Solución
Lo que esto significa es que si te dan dos lados de un triángulo rectángulo, siempre puedes encontrar el tercero. Por lo tanto, si sabes que dos lados de un triángulo rectángulo son congruentes con dos lados de otro triángulo rectángulo, entonces puedes concluir que los terceros lados también son congruentes. Si tres pares de lados son congruentes, entonces sabemos que los triángulos son congruentes por SSS.
Ejemplo\(\PageIndex{3}\)
¿Qué información adicional necesitarías para probar que estos dos triángulos eran congruentes usando el Teorema de HL?
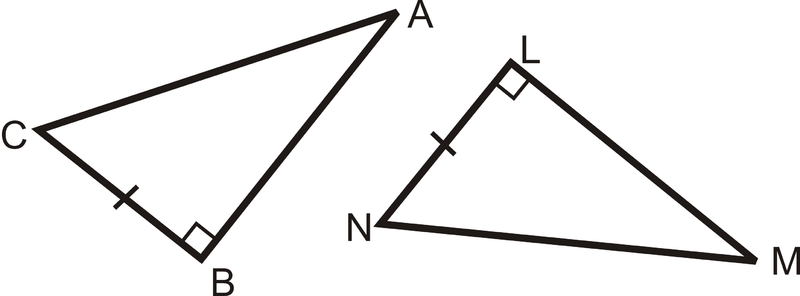
Solución
Para el HL, se necesita que las hipotenusas sean congruentes. \(\overline{AC}\cong MN\overline{AB}\).
Ejemplo\(\PageIndex{4}\)
Determinar si los triángulos son congruentes. Si lo son, escribe la declaración de congruencia y qué congruencia postula o teorema utilizaste.
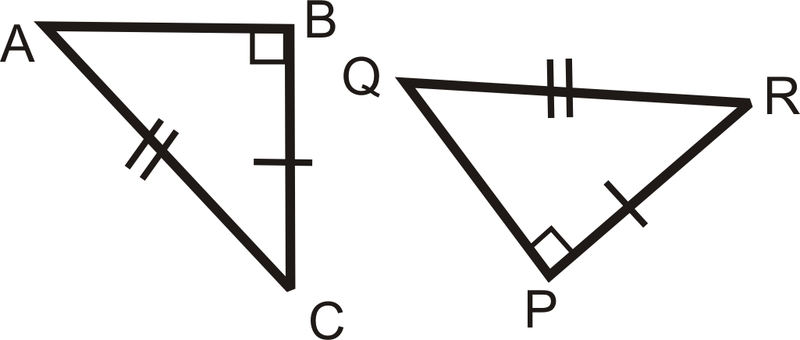
Solución
Sabemos que los dos triángulos son triángulos rectos. Los tienen un par de piernas que es congruente y sus hipotenusas son congruentes. Esto quiere decir que\(\Delta ABC\cong \Delta RQP\) por HL.
Ejemplo\(\PageIndex{5}\)
Determinar la información adicional necesaria para mostrar que los dos triángulos son congruentes por HL.
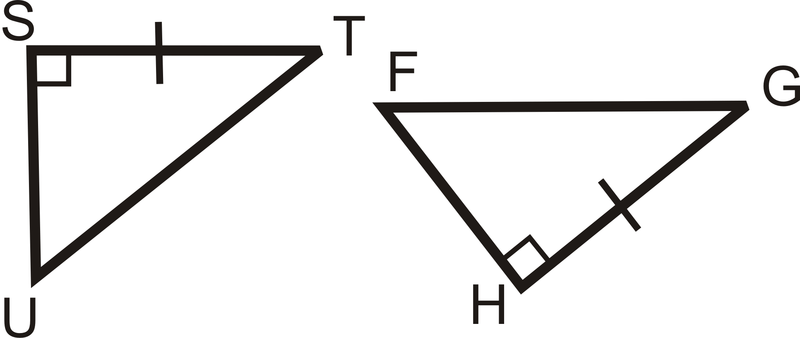
Solución
Ya sabemos que un par de patas es congruente y que son triángulos rectos. El dato adicional que necesitamos es que las dos hipotenusas son congruentes,\(\overline{UT}\cong \overline{FG}\).
Revisar
Utilizando el Teorema HL, ¿qué información adicional necesitas para probar que los dos triángulos son congruentes?
-
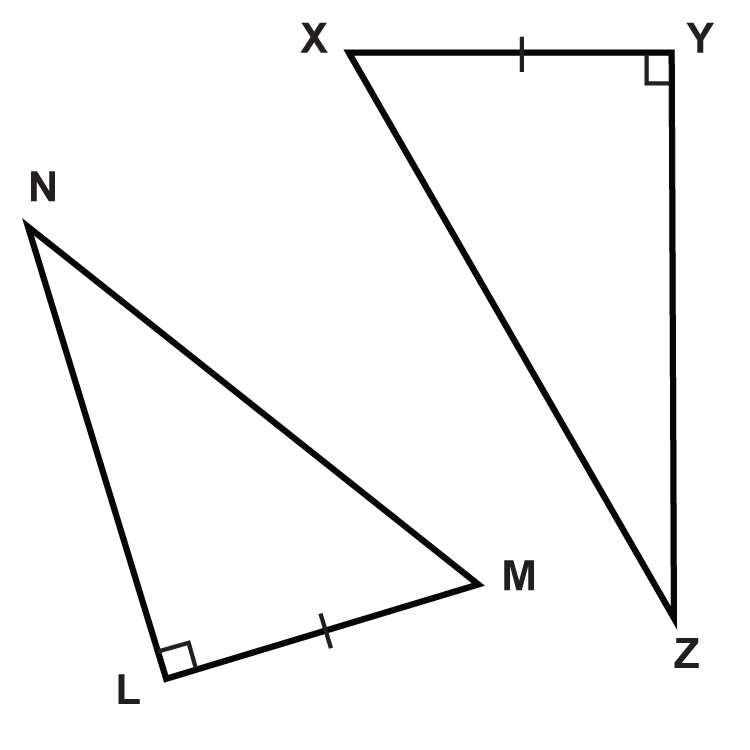
Figura\(\PageIndex{7}\) -
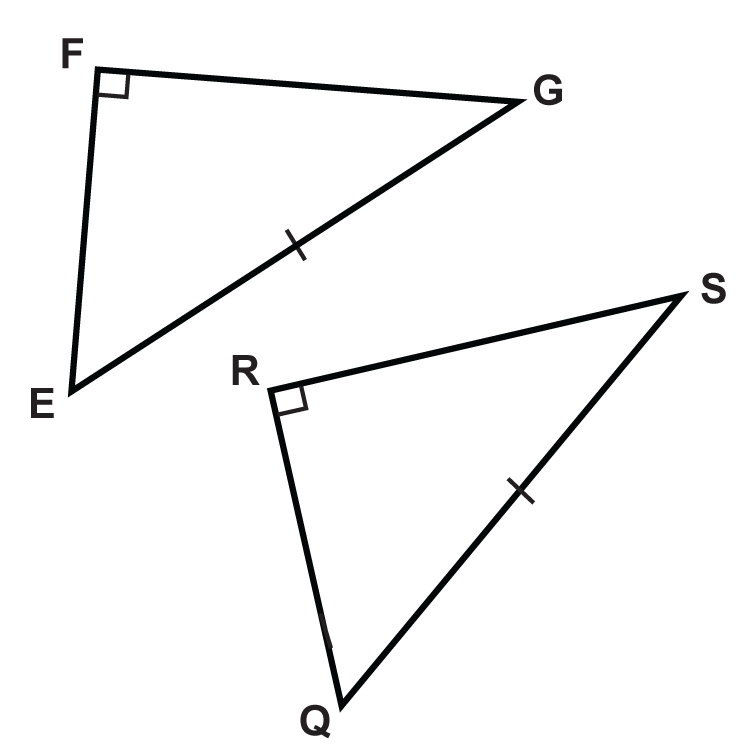
Figura\(\PageIndex{8}\) -
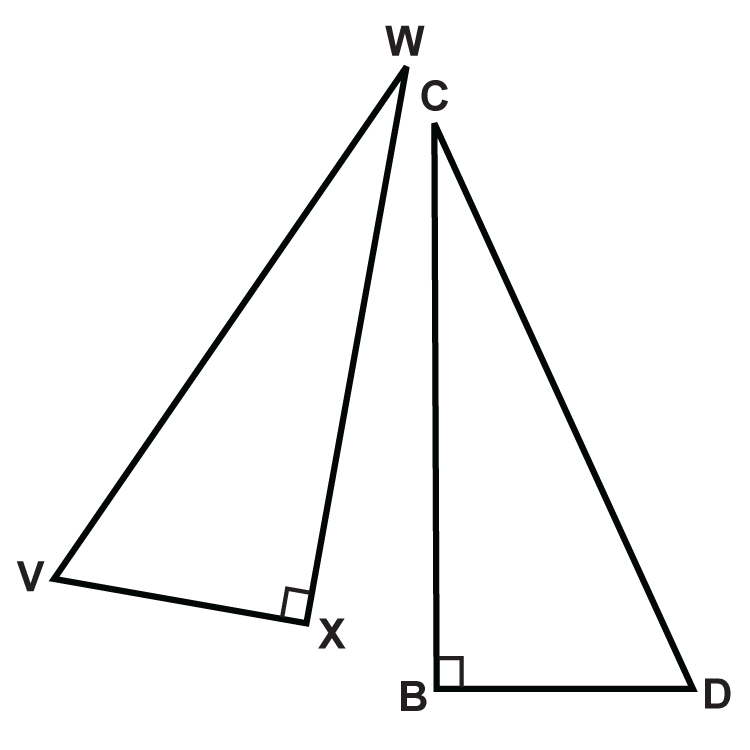
Figura\(\PageIndex{9}\)
Los triángulos están formados por dos líneas paralelas cortadas por una transversal perpendicular. \(C\)es el punto medio de\(\overline{AD}\). Completa la prueba para mostrar que los dos triángulos son congruentes. Las preguntas 4-7 están dentro de la prueba.
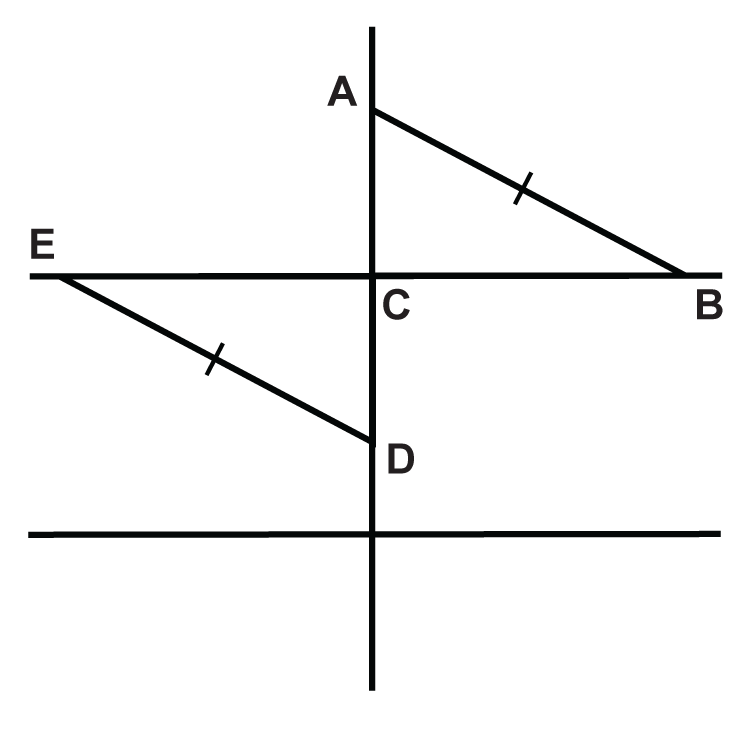
| Declaración | Razón |
|---|---|
| 1. \(\angle ACB\)y\(\angle DCE\) son ángulos rectos. | (4.) |
| 2. (5.) | Definición de punto medio |
| 3. (6.) | Dado |
| 4. \(\Delta ACD\cong \Delta DCE\) | (7.) |
Con base en los siguientes detalles, ¿los dos triángulos rectos son definitivamente congruentes? Las declaraciones no se construyen unas de otras.
- Las hipotenusas de dos triángulos rectos son congruentes.
- Ambos conjuntos de patas en los dos triángulos rectos son congruentes.
- Un juego de patas son congruentes en los dos triángulos rectos.
- Las hipotenusas y un par de patas son congruentes en los dos triángulos rectos.
- Uno de los ángulos no rectos de los dos triángulos rectos es congruente.
- Todos los ángulos de los dos triángulos rectos son congruentes.
- Todos los lados de los dos triángulos rectos son congruentes.
- Ambos triángulos tienen una pierna que es el doble de longitud que la otra.
Recursos
El vocabulario
| Término | Definición |
|---|---|
| hipotenusa | El lado opuesto al ángulo recto en un triángulo rectángulo. |
| piernas | Los dos lados adyacentes al ángulo recto. |
| triángulo rectángulo | Un triángulo con exactamente un ángulo recto (\(90^{\circ}\)). Los dos lados adyacentes al ángulo recto se llaman patas y el lado opuesto al ángulo recto se llama hipotenusa. |
| Teorema de Congruencia H-L (Hipotenusa-Pierna) | Si la hipotenusa y la pierna en un triángulo rectángulo son congruentes con la hipotenusa y la pierna en otro triángulo rectángulo, entonces los dos triángulos son congruentes. |
Recursos adicionales
Elemento Interactivo
Video: Principios de Congruencia del Triángulo HL - Básico
Actividades: HL Triángulo Congruencia Discusión Preguntas
Ayudas de estudio: Guía de estudio de congruencia triangular
Práctica: HL
Mundo real: Borradores finales

