5.5: Área de Cuadrados y Rectángulos
- Page ID
- 107528
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\(\newcommand{\longvect}{\overrightarrow}\)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Encuentra el área de cuadrados y rectángulos usando fórmulas: tiempos base altura y lado cuadrado.

Allen compró una casa nueva y planea reemplazar la alfombra en dos de las recámaras. Un dormitorio tiene forma de cuadrado y el otro es rectangular. Necesita averiguar cuánta alfombra se necesita para cubrir ambos pisos de recámara.
El dormitorio cuadrado tiene longitudes laterales de 9 pies.

El dormitorio rectangular tiene una longitud de 12 pies y un ancho de 8 pies.

Para que Allen pueda averiguar cuánta alfombra necesita comprar para estas dos recámaras, necesita encontrar el área de cada recámara.
En este concepto, aprenderás a encontrar el área de cuadrados y rectángulos.
Área
El espacio interior de una figura se conoce como el área de la figura. Mojar un piso, pasto en el suelo o cualquier otra cosa que cubra el espacio dentro de una figura son ejemplos de área.
Existe una fórmula para encontrar el área de diferentes formas. En este concepto, este concepto te mostrará cómo encontrar el área tanto de cuadrados como de rectángulos.
Esta es la fórmula utilizada para encontrar el área de un cuadrado:
\(A=s\cdot s\)
Recuerda, el punto es otro símbolo para la multiplicación. Para averiguar el área de la plaza, multiplique un lado por el otro lado. Dado que todos los lados en un cuadrado son iguales, los dos números serán los mismos. La unidad de medida se mantiene en la ecuación para ayudarte a recordar cuál debe ser la etiqueta correcta.
Aquí se explica cómo usar la fórmula para encontrar el área de un cuadrado:
\(A=6\text{ ft }\cdot 6\text{ ft }\)
Ahora bien, piense en la ecuación como multiplicar dos cosas distintas; los números y las unidades de medida.
\(A=6\cdot 6\)
\(A=ft\cdot\text{ ft }\)
Resuelve ambas ecuaciones.
\(A=6\times 6=36\)
\(A=ft\times\text{ ft }=ft^2\)
Piensa en lo que sabes de los exponentes. Cuando multiplicas dos de la misma cosa juntos, puedes escribirlo en forma exponencial. Otra forma de etiquetar el área es escribir pies cuadrados (pies cuadrados).
La respuesta es\(36\: sq.\:\text{ ft }.\) o\(36\:\text{ ft }^2\)
Esta es la fórmula utilizada para encontrar el área de un rectángulo:
\(A=lw\)
Para encontrar el área de un rectángulo, use las medidas de largo y ancho en lugar de largo lateral. Estos números pueden ser diferentes entre sí porque no todos los rectángulos tienen las mismas longitudes de lado como lo hacen los cuadrados.

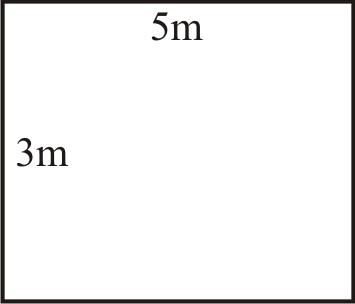
Este rectángulo mide una longitud de 5 metros y una anchura de 3 metros. Al igual que la fórmula de área para un cuadrado, multiplica esos dos números para encontrar el área del rectángulo. Recuerde, dos variables una al lado de la otra en una ecuación indican multiplicación, al igual que el símbolo de punto o símbolo de multiplicación tradicional. Los símbolos se utilizarán indistintamente.
Para encontrar el área de un rectángulo, multiplique la longitud por la anchura.
\(A=5\text{ m }\cdot 3\text{ m }\)
\(A=5\times 3\)
\(A=meters\times meters\)
La fórmula muestra 5 metros por 3 metros. Multiplique la parte de medición (\(5 \times 3\)), luego multiplique las unidades de medida.
La respuesta es\(15\text{ sq. m }\) o\(15 \text{ m}^2\).
La etiqueta para el área de un rectángulo es similar a la etiqueta para el área de un cuadrado desde arriba. La etiqueta puede ser escrita en forma exponencial o escrita en abreviatura.
Ejemplo\(\PageIndex{1}\)
Antes, te dieron un problema sobre Allen y su nueva casa que quiere volver a tapar.
Las dimensiones de las dos habitaciones de Allen se dan en el inicio del concepto. Su habitación cuadrada tiene longitudes laterales de 9 pies. La otra habitación es un rectángulo con dimensiones de 12 pies por 8 pies. Para comenzar a resolver este problema, encuentra el área de cada una de las recámaras.
Solución
El dormitorio cuadrado tiene una longitud lateral de 9 pies.
\(A=s\cdot s\)
\(A=9\times 9=81\text{ sq. feet }\)
El dormitorio cuadrado tiene una superficie de 81 pies cuadrados.
El dormitorio rectangular tiene una longitud de 12 pies y un ancho de 8 pies.
\(A=12\:\text{ ft }\cdot 8\:\text{ ft }\)
\(A=12\times 8\)
\(A=feet\times feet\)
El dormitorio rectangular tiene una superficie de 96 pies cuadrados.
Allen quiere que el área total de sus dos recámaras sepa cuánta alfombra comprar, así que suma las dos áreas juntas.
\(81+96=177\text{ square feet }\)
La respuesta es de 177 pies cuadrados.
Ejemplo\(\PageIndex{2}\)
Encuentra el área de un rectángulo con una longitud de 7\ texto {ft}. y un ancho de 4\ texto {ft}.
Solución
Primero, escribe la ecuación
\(A=lw\)
\(A=7\:\text{ ft }\cdot 4\:\text{ ft }\)
A continuación, multiplique los dos números.
\(A=7\cdot 4=28\)
Después, multiplique las unidades de medida.
\(A=\text{ ft }\cdot\text{ ft }=\text{ ft}^2 \)
Ahora, junta tu respuesta para mostrar la solución final.
\(A=28\text{ ft }^2\)
La respuesta es\(28\: sq.\:\text{ ft }\).
Una vez que hagas más ejemplos puedes encontrarte omitiendo el paso de multiplicar las unidades de medida. Esto puede llegar a ser natural para cuadrar la unidad de medida para cualquier problema de área.
Ejemplo\(\PageIndex{3}\)
Encuentra el área de un cuadrado con longitudes laterales de 10 pulgadas.
Solución
Primero, escribe tu ecuación.
\(A=s\cdot s\)
\(A=10 \text{ in }\cdot 10 \text{ in}\)
A continuación, resuelve la ecuación multiplicando las dos longitudes laterales.
\( A=10\cdot 10=100\)
Entonces, escribe tu solución final. Recuerde escribir la unidad de medida cuadrada después de la respuesta numérica.
\(A=100\text{ in}^2\)
La respuesta es de 100 sq. in.
Ejemplo\(\PageIndex{4}\)
Encuentra el área de un rectángulo con una longitud de 6 pies y un ancho de 5 pies.
Solución
Primero, escribe tu ecuación.
\(A=lw\)
\(A=6\:\text{ ft }\cdot 5\:\text{ ft }\)
A continuación, resuelve la ecuación multiplicando la longitud por la anchura.
\(A=6\cdot 5=30\)
Entonces, escribe tu solución final. Recuerde escribir la unidad de medida cuadrada después de la respuesta numérica.
\( A=30\:\text{ ft }^2\)
La respuesta es de 30 sq. \ text {ft}.
Ejemplo\(\PageIndex{5}\)
Encuentra el área de un rectángulo con una longitud de 9 metros y un ancho de 8 metros.
Solución
Primero, escribe tu ecuación.
\(A=lw\)
\(A=9\text{ m }\cdot 8\text{ m }\)
A continuación, resuelve la ecuación multiplicando la longitud por la anchura.
\(A=9\cdot 8=72\)
Entonces, escribe tu solución final. Recuerde escribir la unidad de medida cuadrada después de la respuesta numérica.
\(A=72\text{ m }^2\)
La respuesta es de 72 metros cuadrados
Revisar
Encuentra el área de cada una de las siguientes figuras. Asegúrate de etiquetar tu respuesta correctamente.
- Un cuadrado con una longitud lateral de 6 pulgadas.
- Un cuadrado con una longitud lateral de 4 pulgadas.
- Un cuadrado con una longitud lateral de 8 centímetros.
- Un cuadrado con una longitud lateral de 12 centímetros.
- Un cuadrado con una longitud lateral de 9 metros.
- Un rectángulo con una longitud de 6 pulgadas y un ancho de 4 pulgadas.
- Un rectángulo con una longitud de 9 metros y un ancho de 3 metros.
- Un rectángulo con una longitud de 4 metros y un ancho de 2 metros.
- Un rectángulo con una longitud de 17 pies y un ancho de 12 pies.
- Un rectángulo con una longitud de 22 pies y un ancho de 18 pies.
- Un cuadrado con una longitud lateral de 13 pies.
- Un cuadrado con una longitud lateral de 18 pies.
- Un cuadrado con una longitud lateral de 21 pies.
- Un rectángulo con una longitud de 18 pies y un ancho de 13 pies.
- Un rectángulo con una longitud de 60 pies y un ancho de 27 pies.
- Un rectángulo con una longitud de 57 pies y un ancho de 22 pies.
Recursos
Recurso Adicional
Video: Determinar el área de un rectángulo que involucra números enteros
Práctica: Área de Cuadrados y Rectángulos

