5.4: Perímetro de Cuadrados y Rectángulos
- Page ID
- 107484
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\(\newcommand{\longvect}{\overrightarrow}\)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Utilice fórmulas básicas de cuadrilátero para encontrar medidas de borde totales de cuadriláteros rectilíneos.
Buscar perímetro y área de cuadrados y rectángulos usando fórmulas

Raj tiene una pequeña porción de tierra que quiere convertir en un huerto. No obstante, quiere construir una pequeña barda a su alrededor antes de sembrar algo. Sabe que el área del terreno es de 240 pies cuadrados y que la longitud de un lado es de 15 pies. Para poder construir una barda, también necesita conocer el ancho del terreno. ¿Cómo puede Raj escribir y resolver una ecuación para determinar el ancho de su futuro jardín?
En este concepto, aprenderás a encontrar el perímetro y área de cuadrados y rectángulos usando fórmulas.
Perímetro y Área de Cuadrados y Rectángulos
Una fórmula es un método que se ha demostrado que funciona a la hora de resolver tipos específicos de problemas.
Exploremos algunas de esas fórmulas familiares observando rectángulos, cuadrados, área y perímetro.
El perímetro de una figura es la distancia alrededor de la figura. Perímetro es la suma de todos los lados en un cuadrado o rectángulo. Dado que un rectángulo tiene dos conjuntos de lados paralelos, la fórmula para determinar el perímetro (\(P\)) de un rectángulo es:
\(P=2L+2W\)
\(L=length\: and\: W=width\)
Veamos un ejemplo.
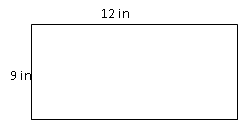
El rectángulo de arriba muestra sus dimensiones. Encuentra el perímetro.
Primero, sustituya los valores de width (\(W\)) y length (\(L\)) en la fórmula perimetral.
\(P=2(12)+2(9)\)
A continuación, completar la multiplicación y suma para encontrar el perímetro.
\(\begin{aligned} P&=2(12)+2(9) \\ P&=24+18 \\ P&=42\end{aligned}\)
La respuesta es 42.
El perímetro del rectángulo es de 42 pulgadas.
Área es la cantidad de unidades cuadradas dentro de la figura. El área se encuentra multiplicando el largo\ por ancho. La fórmula para encontrar el área de un rectángulo es:
\(A=L\times W\)
Puedes usar las dimensiones del rectángulo de arriba para encontrar el área de este rectángulo.
Primero, rellene los valores para\(L\) y\(W\) en la fórmula para área.
\(\begin{aligned} A&=L\times W \\ A&=12\times 9\end{aligned}\)
A continuación, resolver para el área multiplicando.
\(\begin{aligned} A&=12\times 9 \\ A&=108\end{aligned}\)
La respuesta es 108.
El área del rectángulo es\(108\: in^2\).
Observe que la unidad de medida para el área es cuadrada. Eso es porque multiplicaste una unidad de medida por sí misma:\(in\times in=in^2\). El área siempre está escrita en unidades cuadradas.
También se puede encontrar el perímetro y área de una plaza. Recuerde que un cuadrado tiene cuatro lados iguales dado el símbolo s. puede usar la siguiente fórmula para encontrar el perímetro de un cuadrado:
\(P=4s\)
Veamos un ejemplo.
Un rectángulo tiene una longitud de 12 pies y un perímetro de 72 pies. Escribe y resuelve una ecuación para determinar el ancho del rectángulo.
Primero, sustituya los valores para el perímetro (\(P\)) y la longitud (\(L\)) en la fórmula perimetral.
\(72=2(12)+2W\)
A continuación, completa la multiplicación.
\(72=24+2W\)
Después, resta 24 de ambos lados para obtener tu variable sola en el lado derecho.
\(\begin{aligned} 72−24&=24−24+2W \\ 48 &=2W \end{aligned}\)
Después, multiplica ambos lados por el recíproco de 2 para aislar tu variable.
\(\begin{aligned} \dfrac{1}{2}\times \dfrac{48}{1} &=\dfrac{1}{2}\times \dfrac{2W}{1} \\ \dfrac{48}{2}&=W \\ W&=24\end{aligned}\)
La respuesta es 24.
El ancho del rectángulo es de 24 pies.
Ejemplo\(\PageIndex{1}\)
Antes, te dieron un problema sobre Raj y su barda de jardín.
Sabe que el área del terreno es de 240 pies cuadrados, la longitud de un lado es de 15 pies, y necesita saber el ancho del terreno.
Solución
Primero, sustituya los valores para el área y la longitud lateral en la fórmula de área.
\(\begin{aligned} A&=L\times W \\ 240\text{ ft}^2 &=15\text{ ft } \times W\end{aligned}\)
A continuación, multiplique ambos lados por el recíproco de 15 para aislar la variable W.
\(\begin{aligned} \dfrac{1}{15}\times \dfrac{240}{1}&=\dfrac{1}{15}\times \dfrac{15}{1} \times W \\ W&=16 \end{aligned}\)
La respuesta es 16.
El ancho del jardín de Raj es de 16 pies. Por lo tanto, las dimensiones del jardín son 16 ft por 15 ft.
Ejemplo\(\PageIndex{2}\)
Un cuadrado tiene un perímetro de 196 pulgadas. Determinar la longitud de un lado del cuadrado.
Solución
Primero, sustituya el valor del perímetro (\(P\)) en la fórmula perimetral.
\(196=4s\)
A continuación, multiplica ambos lados por el recíproco de 4 para aislar tu variable.
\(\begin{aligned} \dfrac{1}{4}\times \dfrac{196}{1}&=\dfrac{1}{4}\times \dfrac{4s}{1} \\ \dfrac{196}{4}&=s \\ s&=49 \end{aligned}\)
La respuesta es 49.
Ejemplo\(\PageIndex{3}\)
Encuentra el perímetro del siguiente cuadrado si la longitud lateral es\(4.5\: inches\).
Solución
Primero, sustituya el valor de la longitud lateral en la fórmula perimetral.
\(\begin{aligned} P&=4s \\ P&=4(4.5) \end{aligned}\)
A continuación, multiplicar por 4 para resolver para el perímetro.
\(\begin{aligned} P&=4(4.5) \\ P&=18 \end{aligned}\)
La respuesta es 18.
Ejemplo\(\PageIndex{4}\)
¿Puedes encontrar el área de la plaza en el Ejemplo 1?
Solución
Primero, sustituya el valor de la longitud lateral en la fórmula de área.
\(\begin{aligned} A&=s\times s \\ A&=4.5\times 4.5 \end{aligned}\)
A continuación, multiplicar para resolver por el área.
\(\begin{aligned} A&=4.5\times 4.5 \\ A&=20.25\end{aligned}\)
La respuesta es 20.25.
El área de la plaza es\(20.25\text{ in}^2\).
Ejemplo\(\PageIndex{5}\)
Una plaza tiene una superficie de 144 metros cuadrados. ¿Cuál es la longitud lateral?
Solución
Primero, sustituya el valor del área en la fórmula de área.
\(\begin{aligned} A&=s\times s \\ 144\text{ m}^2 &=s\times s \end{aligned}\)
A continuación, tomar la raíz cuadrada de la zona para aislar\(s\). Recuerda que lo opuesto al cuadrado es la raíz cuadrada.
\(\begin{aligned} 144&=s\times s \\ 144&=s^2 \\ s&=\sqrt{144} \\ s&=12 \end{aligned}\)
La respuesta es 12.
Revisar
Encuentra el área y perímetro de cada cuadrado o rectángulo usando fórmulas y las dimensiones dadas. Cada problema tendrá dos respuestas.
- Un cuadrado con una longitud lateral de 5 pulgadas.
- Un rectángulo con una longitud de 5 pulgadas y un ancho de 3 pulgadas.
- Un rectángulo con una longitud de 8 cm y un ancho de 6 cm.
- Un cuadrado con una longitud lateral de 11 pies.
- Un rectángulo con una longitud de 9 pulgadas y un ancho de 4.5 pulgadas.
- Un cuadrado con una longitud lateral de 7 pies.
- Un rectángulo con una longitud de 12 metros y un ancho de 11 metros.
- Un cuadrado con una longitud lateral de 13 metros.
- Un rectángulo con una longitud de 15 pies y un ancho de 8 pies.
- Un cuadrado con una longitud lateral de 12.5 pies.
Encuentra la longitud lateral faltante dada el área de cada cuadrado.
- \(A=64\text{ in}^2\)
- \(A=36\text{ in}^2\)
- \(A=81\text{ m}^2\)
- \(A=100\text{ in}^2\)
- \(A=144\text{ ft}^2\)
- \(A=121\text{ cm}^2\)
- \(A=4\text{ mm}^2\)
Reseña (Respuestas)
Para ver las respuestas de Revisar, abra este archivo PDF y busque la sección 1.13.
vocabulario
| Término | Definición |
|---|---|
| Área | Área es el espacio dentro del perímetro de una figura bidimensional. |
| Fórmula | Una fórmula es un tipo de ecuación que muestra la relación entre diferentes variables. |
| Perimetral | El perímetro es la distancia alrededor de una figura bidimensional. |
| Unidad Cuadrada | Una Unidad Cuadrada es un cuadrado con cuatro lados que cada uno mide 1 unidad. |
Recursos adicionales
Elemento interactivo
Video: Determinar el área de un rectángulo que involucra números enteros
Práctica: Perímetro de Cuadrados y Rectángulos
Mundo real: Una puntada en el tiempo

