5.6: Dimensiones desconocidas de cuadrados y rectángulos
- Page ID
- 107524
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\(\newcommand{\longvect}{\overrightarrow}\)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Calcular medidas lineales, medidas de borde o superficie dadas de cuadriláteros rectilíneos.

Andrea sale de compras navideñas con su mamá y ve una venta en luces navideñas. Ella le pregunta a su mamá si puede conseguir que algunos se encorden alrededor del perímetro de su habitación. Su mamá está de acuerdo, así que miran los paquetes para tratar de averiguar cuántos van a necesitar. La mamá de Andrea no puede recordar las dimensiones exactas de la habitación de Andrea, pero recuerda que es de 81 pies cuadrados y es un cuadrado. ¿Cómo puede Andrea averiguar cuántos pies de luces navideñas necesita?
En este concepto, aprenderás a usar fórmulas para resolver dimensiones desconocidas cuando se le da perímetro o área.
Búsqueda de cotas desconocidas mediante fórmulas
El perímetro es la distancia alrededor de una figura. Área es el número de unidades cuadradas contenidas dentro de una figura. Los perímetros y áreas de rectángulos y cuadrados se pueden encontrar usando las fórmulas a continuación.
- Perímetro Rectangular:\(P=2l+2w\)
- Perímetro Cuadrado:\(P=4s\)
- Área del rectángulo:\(A=lw\)
- Área Cuadrada:\(A=s^2\)
Una ecuación es una oración matemática que dice que dos expresiones matemáticas son iguales. Las fórmulas de perímetro y área anteriores son ejemplos de ecuaciones. Las variables en estas ecuaciones son\(P\)\(A\),\(l\),\(w\), y\(s\).
En ocasiones conocerás el área o perímetro de un rectángulo o un cuadrado, pero no conocerás información sobre todos sus lados. En este caso, puedes sustituir la información que conoces en la fórmula relevante y resolver por el valor desconocido. Recuerda que cuando resuelves una ecuación estás buscando el valor de la variable que iguale a ambos lados de la ecuación.
Aquí hay un ejemplo.
El ancho de un rectángulo es de 10 pies y el perímetro es de 50 pies. ¿Cuál es la longitud del rectángulo?
Primero, averiguar qué fórmula es relevante. Esta pregunta es sobre el perímetro de un rectángulo, por lo que estarás usando la fórmula del perímetro del rectángulo.
\(P=2l+2w\)
A continuación, averigua para qué variables tienes valores y para qué variable estás resolviendo. El problema dice que el ancho es de 10 pies, por lo que w=10. El problema también dice que el perímetro es de 50 pies, entonces\(P=50\). Estás resolviendo para la longitud.
\( \begin{aligned} P&=50 \\ l&=?\\ w&=10\end{aligned}\)
Ahora, sustituya los valores por\(P\) y\(w\) en la fórmula y simplifique.
A continuación, resolver la ecuación. Recuerda que estás buscando el valor de l que haga iguales ambos lados de la ecuación. Primero, averiguar el valor de la\(2l\) en la ecuación. Hazte una pregunta.
“¿50 es igual a qué número más 20?”
Entonces, contesta tu pregunta. 30 más 20 es igual a 50, por lo que\(2l\) debe ser igual a 30.
Ahora, tienes una ecuación más simple que resolver.
\(2l=30\)
A continuación, hágase otra pregunta.
“2 veces ¿qué número es igual a 30?”
Por último, contesta tu pregunta. 2 veces 15 es igual a 30, entonces l debe ser igual a 15.
La respuesta es que la longitud del rectángulo es de 15 pies.
Puede verificar su respuesta sustituyendo los tres valores en la fórmula del perímetro del rectángulo, evaluando y asegurándose de que ambos lados de la ecuación terminen iguales entre sí.
La respuesta es correcta.
Aquí hay otro ejemplo.
Si el área de una plaza es de 144 millas cuadradas, ¿cuál es la longitud de uno de los lados de la plaza?
Primero, averiguar qué fórmula es relevante. Esta pregunta es sobre el área de un cuadrado, por lo que estará usando la fórmula de área cuadrada.
\(A=s^2\)
A continuación, averigüe para qué variable tiene un valor y para qué variable está resolviendo. El problema dice que el área es de 144 millas cuadradas, por lo que A=144. Estás resolviendo para la longitud del lado.
Ahora, sustituya el valor de A en la fórmula.
A continuación, resolver la ecuación. Recuerda que estás buscando el valor de s que haga iguales ambos lados de la ecuación. Hazte una pregunta.
“¿144 es igual a qué número veces sí mismo?”
Entonces, contesta tu pregunta. 12 veces 12 es igual a 144, por lo que s debe ser igual a 12.
La respuesta es que la longitud lateral de la plaza es de 12 millas.
Ahora, verifique su respuesta sustituyendo ambos valores en la fórmula de área cuadrada, evaluando y asegurándose de que ambos lados de la ecuación terminen iguales entre sí.
La respuesta es correcta.
Ejemplo\(\PageIndex{1}\)
Antes, te dieron un problema sobre Andrea y las luces navideñas.
Ella está comprando algunos para encordar alrededor del perímetro de su habitación y necesita saber cuántos pies de luces comprar. Ella sabe que su habitación cuadrada tiene una superficie de 81 pies cuadrados.
Solución
Primero, averiguar la longitud de cada lado de su habitación. Su habitación es una plaza y conoces su área, por lo que estarás usando la fórmula de área cuadrada.
\(A=s^2\)
Ahora bien, ya sabes que el área de la plaza es de 81 pies cuadrados, entonces\(A=81\). Sustituya este valor por A en la fórmula.
A continuación, hágase una pregunta para ayudar a resolver la ecuación.
“¿81 es igual a qué número veces sí mismo?”
Entonces, contesta tu pregunta. 9 veces 9 es igual a 81, por lo que s debe ser igual a 9. Cada lado de la habitación de Andrea mide 9 pies.
Ahora, necesitas averiguar el perímetro de la habitación de Andrea para que Andrea sepa cuántos pies de luces necesita. Sabes que la habitación es una plaza con una longitud lateral de 9 pies. Sustituye s=9 en la fórmula perimetral cuadrada.
La respuesta es que el perímetro de su habitación es de 36 pies, por lo que necesita 36 pies de luces.
Ejemplo\(\PageIndex{2}\)
La familia Hegazzi está diseñando un jardín de verano basado en el modelo que se muestra a continuación. La parte inferior de la parcela es un cuadrado y la parte superior de la parcela es un rectángulo. Si el área total de ambas parcelas en el jardín es de 139 pies cuadrados, ¿cuál es la longitud de un lado de la parcela cuadrada (indicado con un signo de interrogación a continuación)?
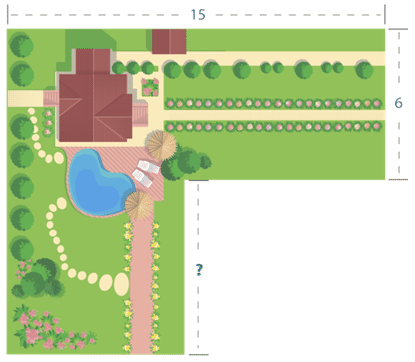
Solución
Primero, use la información dada para encontrar el área de la parcela rectangular. Luego utilizará esta información para ayudarle a encontrar el área de la parcela cuadrada, lo que le permitirá encontrar la longitud lateral de la parcela cuadrada.
El rectángulo tiene una longitud de 15 pies y un ancho de 6 pies. La fórmula para encontrar el área de un rectángulo es\(A=lw\). Sustituir los valores de la longitud y el ancho del rectángulo en la fórmula y evaluar para encontrar el área.
A continuación, encuentra el área de la parcela cuadrada. Sabes que el área total es de 139 pies cuadrados y el área del rectángulo es de 90 pies cuadrados. También sabes que el área total es igual al área del rectángulo más el área cuadrada. Sustituir los valores que conozcas en esta relación.
Ahora, resuelve la ecuación haciéndote una pregunta.
“139 es igual a 90 más ¿qué número?”
A continuación, responde la pregunta. 90 más 10 es igual a 100. 100 más 39 es igual a 139. Por lo que 90 más 49 deben ser iguales a 139. El área de la parcela cuadrada es de 49 pies cuadrados.
Ahora, usa el área de la parcela cuadrada para ayudarte a encontrar la longitud lateral de la parcela cuadrada. Sustituya el valor por\(A\) en la fórmula de área cuadrada.
A continuación, resolver la ecuación.
“¿49 es igual a qué número veces sí mismo?”
Entonces, contesta tu pregunta. 7 veces 7 es igual a 49, por lo que s debe ser igual a 7.
La respuesta es que la longitud lateral de la parcela cuadrada es de 7 pies.
Ejemplo\(\PageIndex{3}\)
Si el perímetro de un rectángulo es de 30 pies, con una longitud de 9 pies, ¿cuál es el ancho del rectángulo?
Solución
Primero, averiguar qué fórmula es relevante. Esta pregunta es sobre el perímetro de un rectángulo, por lo que estarás usando la fórmula del perímetro del rectángulo.
\(P=2l+2w\)
A continuación, averigua para qué variables tienes valores y para qué variable estás resolviendo. El problema dice que el perímetro es de 30 pies, así que P=30\). El problema también dice que la longitud es de 9 pies, así que l=9\). Estás resolviendo para el ancho.
\(\begin{aligned} P&=30 \\ l&=9 \\ w&=? \end{aligned}\)
Ahora, sustituya los valores por P y l en la fórmula y simplifique.
A continuación, resolver la ecuación. Primero, averiguar el valor de la\(2w\) en la ecuación. Hazte una pregunta.
“30 es igual a 18 más ¿qué número?”
Entonces, contesta tu pregunta. 18 más 12 es igual a 30, por lo que\(2w\) debe ser igual a 12.
Ahora, tienes una ecuación más simple que resolver.
\(2w=12\)
A continuación, hágase otra pregunta.
“2 veces ¿qué número es igual a 12?”
Por último, contesta tu pregunta. 2 veces 6 es igual a 12, por lo que w debe ser igual a 6.
La respuesta es que el ancho del rectángulo es de 6 pies.
Ahora, verifique su respuesta sustituyendo los tres valores en la fórmula del perímetro del rectángulo, evaluando y asegurándose de que ambos lados de la ecuación terminen iguales entre sí.
La respuesta es correcta.
Ejemplo\(\PageIndex{4}\)
Si el área de un cuadrado es de 225 pies cuadrados, ¿cuál es la longitud de uno de sus lados?
Solución
Primero, averiguar qué fórmula es relevante. Esta pregunta es sobre el área de un cuadrado, por lo que estará usando la fórmula de área cuadrada.
\(A=s^2\)
A continuación, averigüe para qué variable tiene un valor y para qué variable está resolviendo. El problema dice que el área es de 225 pies cuadrados, entonces\(A=225\). Estás resolviendo para la longitud del lado.
Ahora, sustituya el valor de A en la fórmula.
A continuación, resuelve la ecuación haciéndote una pregunta.
“¿225 es igual a qué número veces sí mismo?”
Entonces, contesta tu pregunta. 15 veces 15 es igual a 225, por lo que s debe ser igual a 15.
La respuesta es que la longitud lateral del cuadrado es de 15 pies.
Ahora, verifique su respuesta sustituyendo ambos valores en la fórmula de área cuadrada, evaluando y asegurándose de que ambos lados de la ecuación terminen iguales entre sí.
La respuesta es correcta.
Ejemplo\(\PageIndex{5}\)
Si el perímetro de una plaza es de 24 metros, ¿cuál es la longitud de uno de los lados?
Solución
Primero, averiguar qué fórmula es relevante. Esta pregunta es sobre el perímetro de un cuadrado, por lo que estarás usando la fórmula del perímetro cuadrado.
\(P=4s\)
A continuación, averigüe para qué variable tiene un valor y para qué variable está resolviendo. El problema dice que el perímetro es de 24 metros, entonces\(P=24\). Estás resolviendo para la longitud del lado.
Ahora, sustituya el valor por\(P\) en la fórmula.
A continuación, resuelve la ecuación haciéndote una pregunta.
“¿24 es igual a 4 veces qué número?”
Entonces, contesta tu pregunta. 4 veces 6 es igual a 24, por lo que s debe ser igual a 6.
La respuesta es que la longitud lateral del cuadrado es de 6 metros.
Ahora, verifique su respuesta sustituyendo ambos valores en la fórmula del perímetro cuadrado, evaluando y asegurándose de que ambos lados de la ecuación terminen iguales entre sí.
La respuesta es correcta.
Revisar
Dada la zona, encuentra la longitud lateral para cada cuadrado.
- \(A=16\text{ sq. ft. } \)
- \(A=64\text{ sq. m. } \)
- \(A=100\text{ sq. miles }\)
- \(A=121\text{ sq. inches } \)
- \(A=144\text{ sq. ft. } \)
Dada la superficie y longitud, encuentra el ancho de cada rectángulo.
- \(A=24\text{ sq. feet },\text{ length }=8\text{ feet } \)
- \(A=48 \text{ sq. feet },\text{ length }=12\text{ feet } \)
- \(A=64\text{ sq. feet },\text{ length }=10\text{ feet } \)
- \(A=120\text{ sq. meters },\text{ length }=40\text{ meters } \)
- \(A=130\text{ sq. feet },\text{ length }=13\text{ feet } \)
- \(A=90\text{ sq. inches },\text{ length }=45\text{ inches } \)
Dado el perímetro, encuentra la longitud lateral de cada cuadrado.
- \(P=48\text{ inches } \)
- \(P=64\text{ inches } \)
- \(P=90\text{ inches } \)
- \(P=35\text{ feet } \)
Reseña (Respuestas)
Para ver las respuestas de Revisar, abra este archivo PDF y busque la sección 1.15.
El vocabulario
| Término | Definición |
|---|---|
| Área | Área es el espacio dentro del perímetro de una figura bidimensional. |
| Medición | Una medida es el peso, la altura, la longitud o el tamaño de algo. |
Recursos adicionales
Video: Determinar el área de un rectángulo que involucra números enteros
Práctica: Dimensiones desconocidas de cuadrados y rectángulos
Mundo real: Residuos de patio

