5.12: Estimación del área de paralelogramo en planos a escala
- Page ID
- 107496
Utilice una fórmula y una escala para determinar las dimensiones reales a partir de las cotas de escala.
El pueblo planeaba poner en una fila de canchas de tejo a lo largo de una propiedad en forma de paralelogramo cerca de la casa de Jaxon. Si el dibujo muestra un paralelogramo con una\(15′′\) base y una\(1′′\) altura, y la escala es\(1\text{ inch }=12\text{ feet }\), ¿qué tan grande es toda el área?
En este concepto, aprenderás a estimar el área de un paralelogramo en un dibujo a escala.
Estimación del área de un paralelogramo
Un dibujo a escala es un dibujo que utiliza una pequeña medida para representar la medida real.
Si se le da la escala, puede utilizarla para estimar las áreas reales de un paralelogramo.
Por ejemplo:
Estimar la superficie de este jardín.
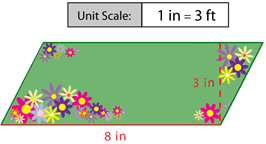
La fórmula para el área de un paralelogramo es\(A=bh\).
Si multiplicas las dimensiones dadas para la base y la altura en el dibujo a escala, obtendrás las pulgadas cuadradas del dibujo, no el área del jardín real. Deberá usar la escala para convertir las dimensiones a sus tamaños reales.
Primero, la escala lee\(1\text{ in }=3\text{ ft }\). Esto significa que cada pulgada en el dibujo representa 3 pies de tierra real. Hay 3 pies por pulgada, así que multiplica la base y la altura dadas por 3.
\(8\text{ in }\times \dfrac{3\text{ ft }}{\text{ in }}\)
Escribiendo la ecuación con dos fracciones, puedes ver que las pulgadas se cancelan, y te quedas con los pies.
\(\dfrac{8 \text{ in }}{1}\times \dfrac{3\text{ ft }}{\text{ in }}=24\text{ ft }\)
Esto significa que la base real es 24\ text {ft}.
\(\dfrac{3 \text{ in }}{1}\times \dfrac{3\text{ ft }}{\text{ in }}=9\text{ ft }\)
Esto significa que la altura real es de 9 pies.
A continuación, redondea esos valores al 10 más cercano.
\(24\approx 20\)
La base aproximada es de 20.
\(9\approx 10\)
La altura aproximada es de 10.
Después, inserta tus aproximaciones en la fórmula.
\(\begin{aligned} A&=bh \\ A&=20′\times 10′ \\ A&=200 \text{ sq ft } \end{aligned}\)
La respuesta es que la estimación es de 200 pies cuadrados.
Puede verificar su estimación insertando las dimensiones reales en la fórmula.
\(\begin{aligned} A&=bh \\ A&=24′\times 9′ \\ A&=216 \text{ sq ft } \end{aligned} \)
El área real es de 216 pies cuadrados.
\(216\approx 200\)
La estimación es razonable.
La estimación puede ayudarte a visualizar el tamaño real de algo y determinar si tu respuesta es correcta o no.
Recuerda que al redondear 4, 5 o 6, es posible que obtengas un área significativamente mayor o menor que la real.
Ejemplo\(\PageIndex{1}\)
Antes, te dieron un problema sobre Jaxon y el plano del área de la cancha de tejo.
Jaxon quiere estimar el tamaño del área real y sabe que la escala es de 1 pulgada = 12 pies. ¿Cuántos pies cuadrados habrá para las canchas si el dibujo tiene una base de 15 pulgadas y una altura de 1 pulgada?
Solución
Primero, determinar las dimensiones reales.
\(\begin{aligned} 15\text{ in }\times \dfrac{12\text{ ft }}{\text{ in }}&=180\text{ ft } \\ b&=180′ \\ 1\text{ in }\times \dfrac{12\text{ ft }}{\text{ in }}&=12\text{ ft } \\ h=12′ \end{aligned}\)
A continuación, redondear los valores y sustituirlos en la fórmula.
\(\begin{aligned} A&=bh \\ A&=180′\times 10′ \\ A=1,800 \text{ sq ft } \end{aligned}\)
La estimación de Jaxon es de 1,800 pies cuadrados.
Luego, encuentra los pies cuadrados reales usando las dimensiones reales.
\(\begin{aligned} A&=180′\times 12′ \\ A&=2,160 \text{ sq ft }\end{aligned}\)
El área real es de 2,160 pies cuadrados.
Ejemplo\(\PageIndex{2}\)
Mirando el mismo dibujo, use una escala de\(1′′=2\text{ feet }\).
Solución
Primero, la escala lee\(1\text{ in }=2\text{ ft }\), o 2 pies por pulgada, así que multiplica la base y la altura dadas por 2.
\(8\text{ in }\times \dfrac{2\text{ ft }}{\text{ in }}=16 \text{ ft }\)
La base real es 16\ text {ft}.
\(3\text{ in }\times \dfrac{2\text{ ft }}{\text{ in }}=6 \text{ ft }\)
Esto significa que la altura real es de 6 pies.
A continuación, redondea esos valores al 10 más cercano.
16 rondas a 20
La base aproximada es de 20.
6 rondas a 10
La altura aproximada es de 10.
Después, inserta tus aproximaciones en la fórmula.
\(\begin{aligned} A&=bh \\ A&=20′\times 10′ \\ A &=200 \text{ sq ft }\end{aligned}\)
La respuesta es que la estimación es de 200 pies cuadrados.
Puede verificar su estimación insertando las dimensiones reales en la fórmula.
\(\begin{aligned} A&=bh \\ A&=16′\times 6′ \\ A&=96 \text{ sq ft } \end{aligned}\)
El área real es de 96 pies cuadrados.
La estimación es alta.
Ejemplo\(\PageIndex{3}\)
Usa una escala de 1′′=4\ text {ft} para estimar el área que tiene una base de 6 pulgadas y una altura de 4 pulgadas.
Solución
Primero, determinar las dimensiones reales.
\(\begin{aligned}6\text{ in }\times \dfrac{4\:\text{ ft }}{\text{ in }}&=24\:\text{ ft } \\ b&=24′ \\ 4\text{ in }\times \dfrac{4\text{ ft }}{\text{ in }}&=16\:\text{ ft } \\ h&=16′ \end{aligned}\)
A continuación, redondear los valores y sustituirlos en la fórmula.
\(\begin{aligned} A&=20′\times 20′ \\ A&=400\text{ sq ft } \end{aligned}\)
La respuesta es que la estimación es de 400 pies cuadrados.
Luego, encuentra los pies cuadrados reales usando las dimensiones reales.
\(\begin{aligned}A&=24′\times 16′ \\ A&=384\text{ sq ft }\end{aligned}\)
El área real es de 384 pies cuadrados.
La estimación es razonable.
Ejemplo\(\PageIndex{4}\)
Estimar el área de un paralelogramo con una base de 59 pulgadas y una altura de 67 pulgadas. Entonces resuelve para el área real.
Solución
Primero, redondear los valores y sustituirlos en la fórmula.
\(\begin{aligned} A&=60′′\times 70′′ \\ A&=420 \text{ sq in }\end{aligned}\)
A continuación, utilice las dimensiones reales en la fórmula.
\(\begin{aligned} A&=59′′\times 67′′ \\ A&=3,953 \text{ sq in }\end{aligned} \)
La respuesta es que el área es de 3,953 pulgadas cuadradas.
Ejemplo\(\PageIndex{5}\)
Un paralelogramo tiene una base de 12 cm y una altura de 9 cm. ¿Cuál es su área?
Solución
Primero, escribe la fórmula.
\(A=bh\)
A continuación, suplente.
\( A=12\text{ cm }\times 9\text{ cm }\)
Entonces, resuelve.
\( A=108\text{ sq cm }\)
La respuesta es de 108 centímetros cuadrados.
Si redondeaste y multiplicaste en tu cabeza, tu estimación debería haber sido de 100 centímetros cuadrados.
Revisar
Para cada paralelogramo, encuentra cada nueva área usando la escala\(1′′=2\text{ feet }\).
- Base de 6 pulgadas, altura de 4 pulgadas
- Base de 8 pulgadas, altura de 6 pulgadas
- Base de 4 pulgadas, altura de 4 pulgadas
- Base de 5 pulgadas, altura de 4 pulgadas
- Base de 6 pulgadas, altura de 6 pulgadas
- Base de 10 pulgadas, altura de 8 pulgadas
- Base de 11 pulgadas, altura de 12 pulgadas
- Base de 15 pulgadas, altura de 9 pulgadas
- Base de 15 pulgadas, altura de 12 pulgadas
Resuelve cada problema.
- Un paralelogramo tiene una superficie de 390 centímetros cuadrados. Si su altura es de 15 cm, ¿cuál es su base?
- ¿Cuál es la altura de un paralelogramo cuya base es de 28 pulgadas y su área es de 1,176 pulgadas cuadradas?
- Donna quiere cubrir su caja de manualidades en forma de paralelogramo en tela. La base de la tapa es de 32.7 cm y la altura es de 12.2 cm. ¿Cuál es el área de la tapa?
- John está plantando pasto en un parche de césped que tiene la forma de un paralelogramo. La altura del paralelogramo es de 34 pies. El otro borde es de 65 pies. ¿Cuántos pies cuadrados de pasto plantará John?
- Kara y Sharice están en una competencia de acolchado. Ambos son colchas cosidas en forma de paralelogramo. Hasta el momento Kara's tiene un área de 2,278 pulgadas cuadradas y una altura de 44 pulgadas. La colcha de Sharice tiene un área de 2,276 pulgadas cuadradas y una altura de 47 pulgadas. ¿De quién es la colcha más larga? ¿Por cuántas pulgadas es más largo?
- Denise compró un marco en forma de paralelogramo. El área del marco es de 36,795 centímetros cuadrados. Si su altura es de 165 centímetros, ¿cuál es su base?
Reseña (Respuestas)
Para ver las respuestas de Revisar, abra este archivo PDF y busque la sección 9.11.
Recursos
vocabulario
| Término | Definición |
|---|---|
| Área | Área es el espacio dentro del perímetro de una figura bidimensional. |
| Paralelogramo | Un paralelogramo es un cuadrilátero con dos pares de lados paralelos. |
| Perímetro | El perímetro es la distancia alrededor de una figura bidimensional. |
| Dibujo a Escala | Un dibujo a escala es un dibujo que se realiza con una escala para que pequeñas unidades de medida específicas representen unidades de medida más grandes. |
Recursos adicionales
Video: Área de un Paralelogramo (Números Enteros)
Práctica: Estimación del área de paralelogramo en planos a escala

