5.13: Trapezoides
- Page ID
- 107539
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Determinar medidas de ángulo desconocido de cuadriláteros con exactamente un par de lados paralelos.
Un trapecio es un cuadrilátero con exactamente un par de lados paralelos.
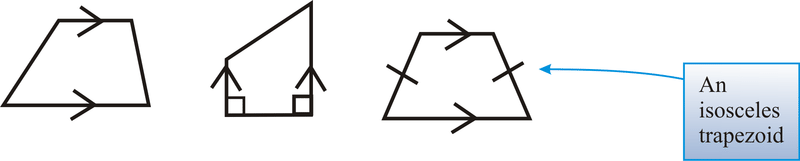
Un trapecio isósceles es un trapecio donde los lados no paralelos son congruentes.
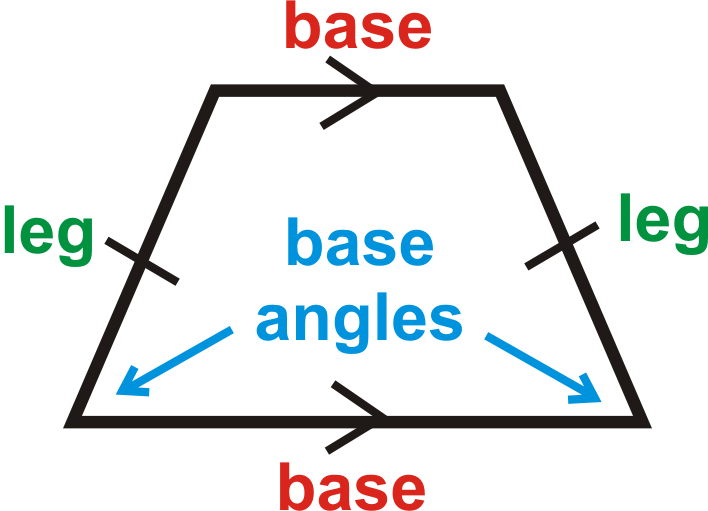
Los ángulos de base de un trapecio isósceles son congruentes. Si\(\(ABCD\)\) es un trapecio isósceles, entonces\(\angle A\cong \angle B\) y\(\angle C\cong \angle D\).
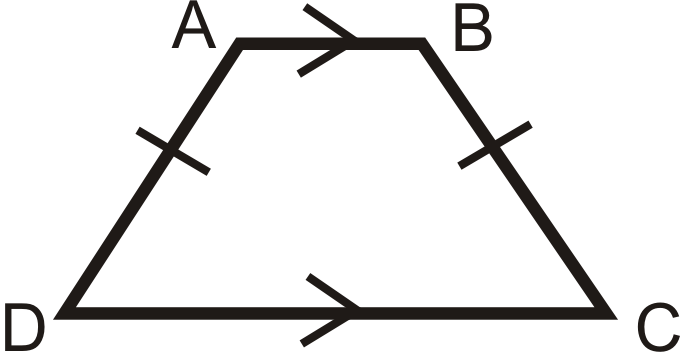
Lo contrario también es cierto. Si un trapecio tiene ángulos de base congruentes, entonces es un trapecio isósceles. Las diagonales de un trapecio isósceles también son congruentes. El segmento medio (de un trapecio) es un segmento de línea que conecta los puntos medios de los lados no paralelos:
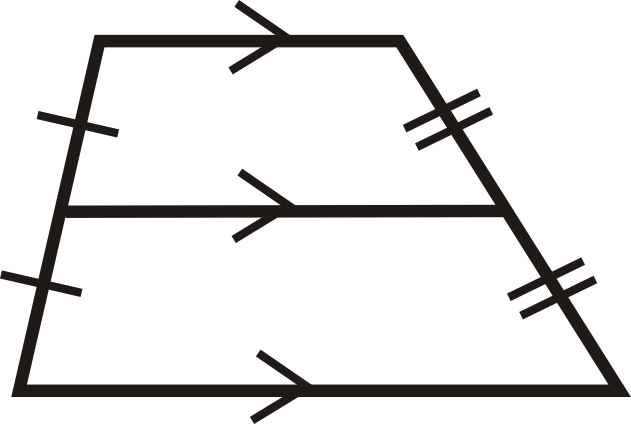
Solo hay un segmento medio en un trapecio. Será paralelo a las bases porque se encuentra a medio camino entre ellas.
Teorema del segmento medio: La longitud del segmento medio de un trapecio es el promedio de las longitudes de las bases.
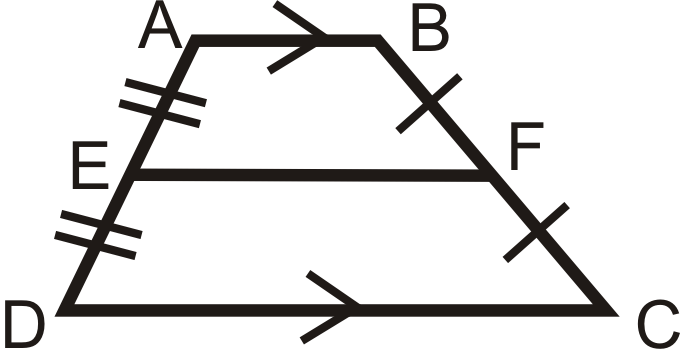
Si\(\overline{EF}\) es el segmento medio, entonces\(EF=\dfrac{AB+CD}{2}\).
¿Y si te dijeran que el polígono\(ABCD\) es un trapecio isósceles y que uno de sus ángulos base mide\(38^{\circ}\)? ¿Qué puedes concluir sobre su otro ángulo base?
Para los Ejemplos 1 y 2, utilice la siguiente información:
\(\(TRAP\)\) es un trapecio isósceles.
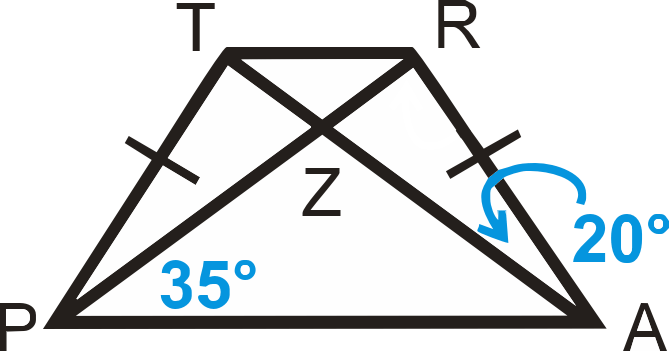
Ejemplo\(\PageIndex{1}\)
Encuentra\(m\angle TPA\).
Solución
\(\angle TPZ\cong \angle RAZ\)así\(m\angle TPA=20^{\circ} +35^{\circ} =55^{\circ}\).
Ejemplo\(\PageIndex{2}\)
Encuentra\(m\angle ZRA\).
Solución
Ya que\(m\angle PZA=110^{\circ}\),\(m\angle RZA=70^{\circ}\) porque forman un par lineal. Por el teorema de la suma del triángulo,\(m\angle ZRA=90^{\circ}\).
Ejemplo\(\PageIndex{3}\)
Mira el trapecio\(TRAP\) a continuación. ¿Qué es\(m\angle A\)?
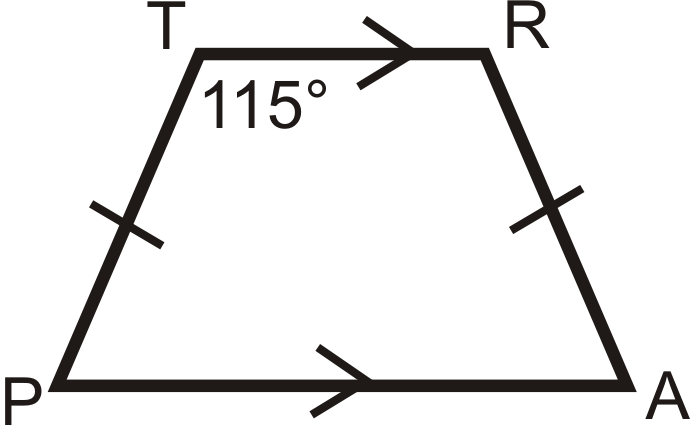
Solución
\(TRAP\)es un trapecio isósceles. \(m\angle R=115^{\circ}\)también.
Para encontrar\ (m\ ángulo, establezca una ecuación.
\ (\ begin {alineado}
115^ {\ circ} +115^ {\ circ} +m\ ángulo A+m\ ángulo P &=360^ {\ circ}\\
230^ {\ circ} +2 m\ ángulo A &=360^ {\ circ}\ cuádruple\ fila derecha m\ ángulo A=m\ ángulo P\\
2 m\ ángulo A &=130^ {\ circ}\\
m\ ángulo A &=65^ {\ circ}
\ final { alineado}\)
Fíjese en eso\(m\angle R+m\angle A=115^{\circ} +65^{\circ} =180^{\circ}\). Estos ángulos siempre serán complementarios debido al Teorema de los Ángulos Interiores Consecutivos.
Ejemplo\(\PageIndex{4}\)
¿Es\(ZOID\) un trapecio isósceles? ¿Cómo lo sabes?
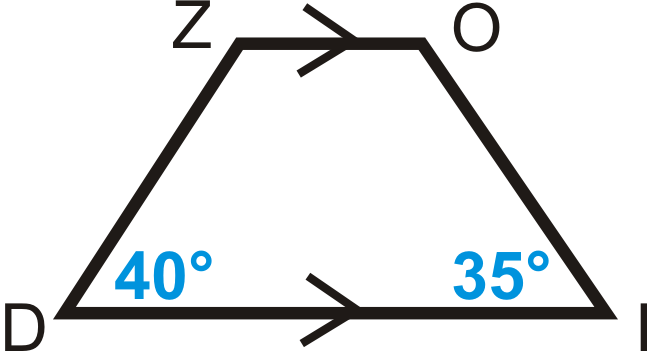
Solución
\(40^{\circ} \neq 35^{\circ}\), no\(ZOID\) es un trapecio isósceles.
Ejemplo\(\PageIndex{5}\)
Encuentra\(x\). Todas las figuras son trapezoides con el segmento medio marcado como se indica.
-
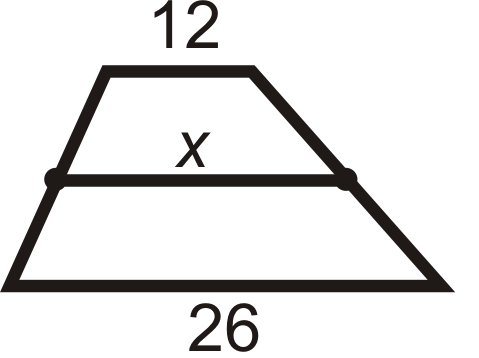
Figura\(\PageIndex{10}\)
-
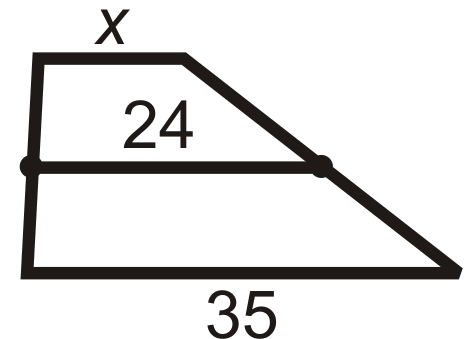
Figura\(\PageIndex{10}\) -
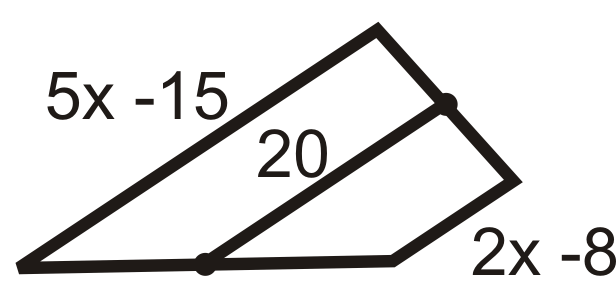
Figura\(\PageIndex{11}\)
Solución
- \(x\)es el promedio de 12 y 26. \(\dfrac{12+26}{2}=\dfrac{38}{2}=19\)
- 24 es el promedio de\(x\) y 35.
\(\begin{aligned} \dfrac{x+35}{2}&=24 \\ x+35&=48 \\ x&=13 \end{aligned}\)
- 20 es el promedio de\(5x−15\) y\(2x−8\).
\(\begin{aligned} \dfrac{5x−15+2x−8}{2}&=20 \\ 7x−23&=40 \\ 7x&=63 \\ x&=9 \end{aligned}\)
Revisar
1. ¿Pueden ser congruentes los lados paralelos de un trapecio? ¿Por qué o por qué no?
Para las preguntas 2-8, encuentra la longitud del segmento medio o lado faltante.
-
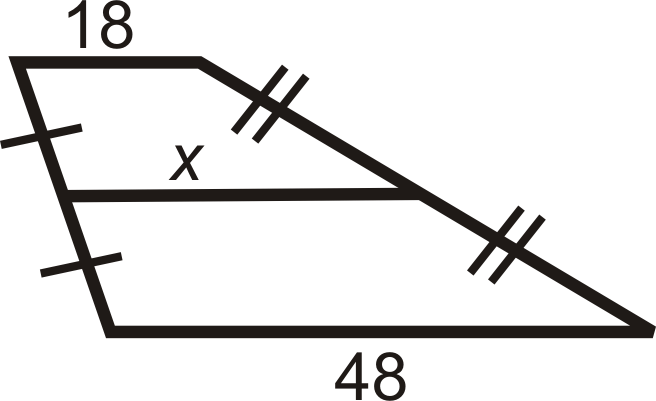
Figura\(\PageIndex{12}\) -
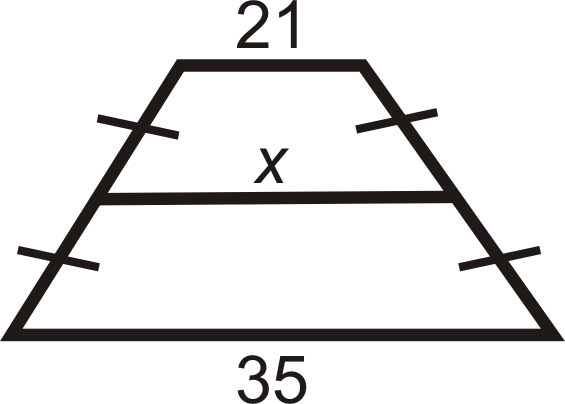
Figura\(\PageIndex{13}\) -
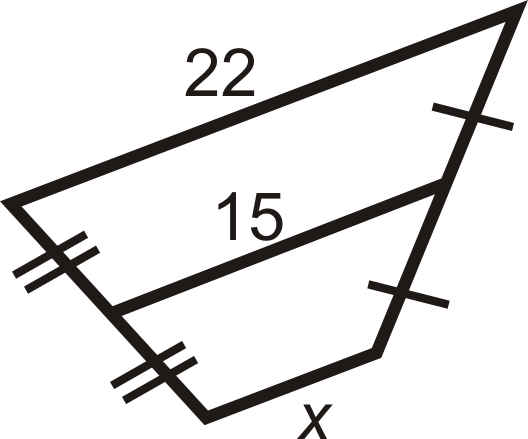
Figura\(\PageIndex{14}\) -
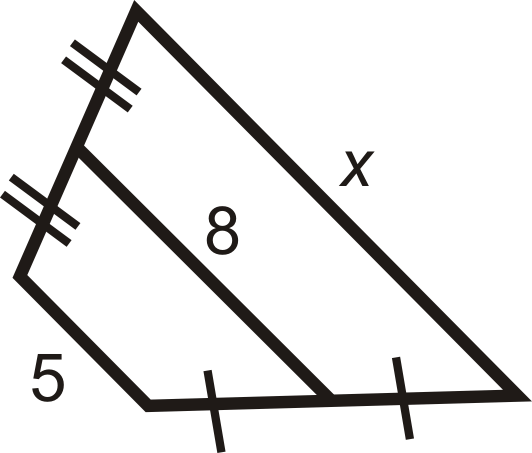
Figura\(\PageIndex{15}\) -
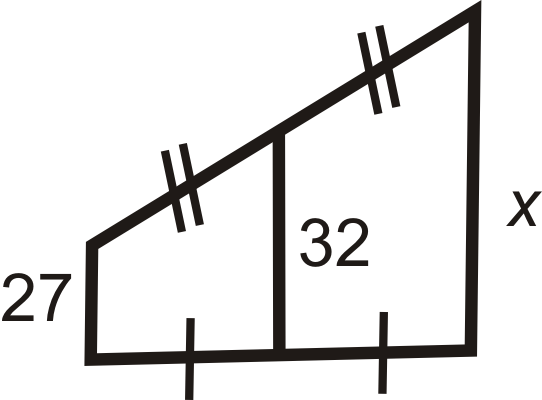
Figura\(\PageIndex{16}\) -
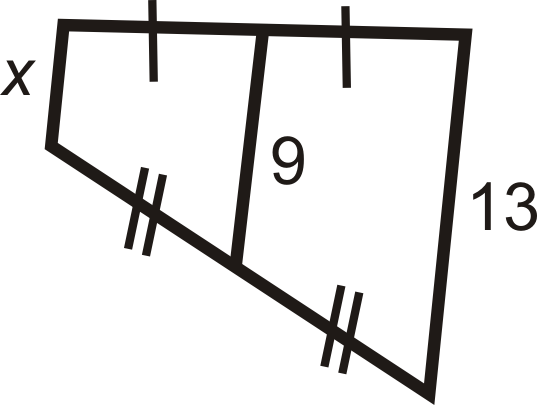
Figura\(\PageIndex{17}\)
Encuentra el valor de la (s) variable (s) faltante (s)
-
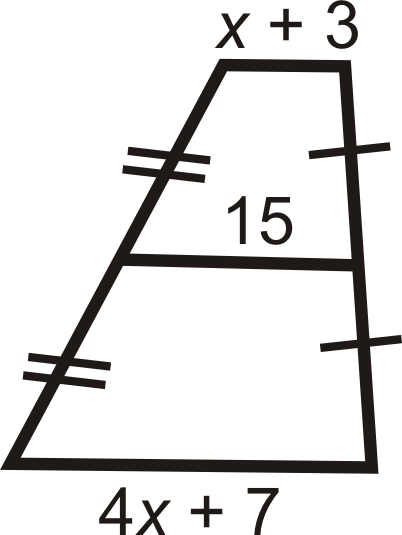
Figura\(\PageIndex{18}\)
Encuentra las longitudes de las diagonales de los trapecios a continuación para determinar si es isósceles.
- A (−3,2), B (1,3), C (3, −1), D (−4, −2)
- A (−3,3), B (2, −2), C (−6, −6), D (−7,1)
Reseña (Respuestas)
Para ver las respuestas de Revisar, abra este archivo PDF y busque la sección 6.6.
El vocabulario
| Término | Definición |
|---|---|
| trapecio isósceles | Un trapecio isósceles es un trapecio donde los lados no paralelos son congruentes. |
| segmento medio (de un trapecio) | Un segmento de línea que conecta los puntos medios de los lados no paralelos. |
| trapecio | Un cuadrilátero con exactamente un par de lados paralelos. |
| Diagonal | Una diagonal es un segmento de línea en un polígono que conecta vértices no consecutivos |
| segmento medio | Un segmento medio conecta los puntos medios de dos lados de un triángulo o los lados no paralelos de un trapecio. |
Recursos adicionales
Elemento Interactivo
Video: Ejemplos de Trapezoides - Básico
Actividades: Preguntas de discusión sobre trapecios
Ayudas de estudio: Guía de estudio de trapecios y cometas
Práctica: Trapecios
Mundo Real: Trapezoides en Tombuctú