5.17: Área y Perímetro de Rombos y Cometas
- Page ID
- 107500
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)El área es la mitad del producto de las diagonales; el perímetro es la suma de los lados.
Recordemos que un rombo es un cuadrilátero con cuatro lados congruentes y una cometa es un cuadrilátero con distintos lados congruentes adyacentes. Ambos cuadriláteros tienen diagonales perpendiculares, que es como vamos a encontrar sus áreas.
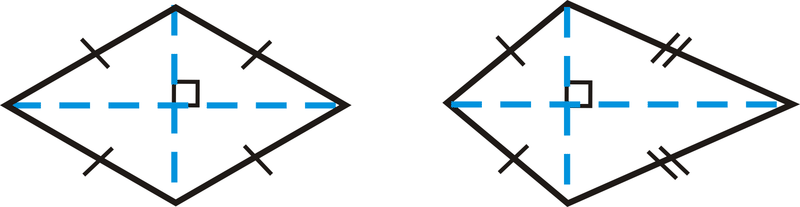
Observe que las diagonales dividen cada cuadrilátero en 4 triángulos. Si movemos los dos triángulos en la parte inferior de cada cuadrilátero para que coincidan con los triángulos por encima de la diagonal horizontal, tendríamos dos rectángulos.
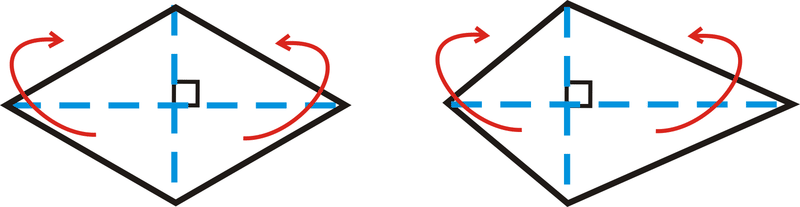
Entonces, la altura de estos rectángulos es la mitad de una de las diagonales y la base es la longitud de la otra diagonal.
El área de un rombo o una cometa es\(A=\dfrac{1}{2}d_1 d_2\)
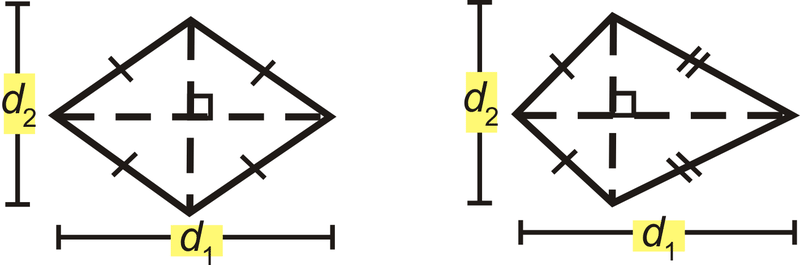
¿Y si te dieran una cometa o un rombo y el tamaño de sus dos diagonales? ¿Cómo podrías encontrar la distancia total alrededor de la cometa o rombo y la cantidad de espacio que ocupa?
Ejemplo\(\PageIndex{1}\)
Encuentra el perímetro y el área de la cometa a continuación.
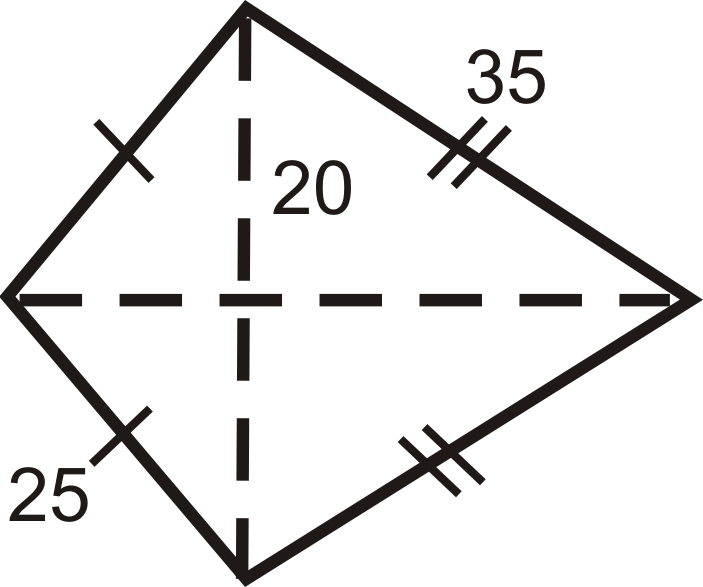
Solución
En una cometa, hay dos pares de triángulos congruentes. Usa el Teorema de Pitágoras para encontrar las longitudes de lados o diagonales.
\(Smaller\: diagonal\: portion\)
\(20^2+d^2_s=25^2\)
\(d^2_s=225\)
\(d_s=15\: units\)
\(Larger\: diagonal\: portion\)
\(20^2+d^2_l=352 \)
\(d^2_l=825\)
\(d_l=5 units\)
\(A=\dfrac{1}{2}(15+5)(40)\cong 874.5 units^2\)
\(P=2(25)+2(35)=120\: units\)
Ejemplo\(\PageIndex{2}\)
Encuentra el área de un rombo con diagonales de 6 in y 8 in.
Solución
El área es\(\dfrac{1}{2}(8)(6)=24 in^2\).
Ejemplo\(\PageIndex{3}\)
Encuentra el perímetro y área del rombo a continuación.
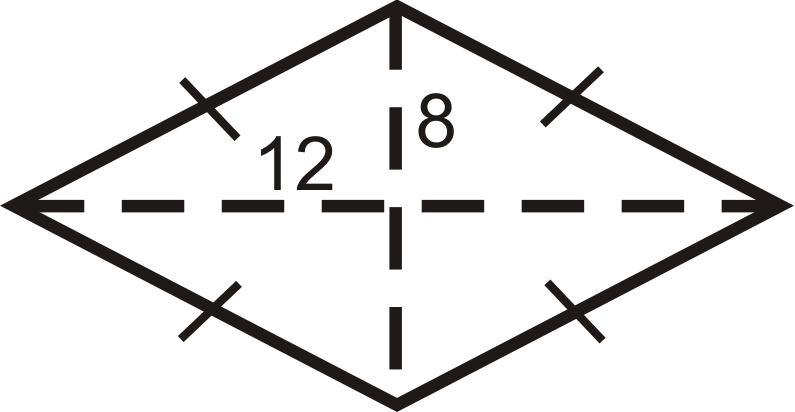
Solución
En un rombo, los cuatro triángulos creados por las diagonales son congruentes.
Para encontrar el perímetro, se debe encontrar la longitud de cada lado, que sería la hipotenusa de uno de los cuatro triángulos. Usa el Teorema de Pitágoras.
\(12^2+8^2=side^2\qquad A=12\cdot 16\cdot 24\)
\(144+64=side^2 \qquad A=192 units^2\)
\(side=\sqrt{208}\)
\(P=4\sqrt{13}=4(4\sqrt{13})=16\sqrt{13} units\)
Ejemplo\(\PageIndex{4}\)
Encuentra el perímetro y área del rombo a continuación.
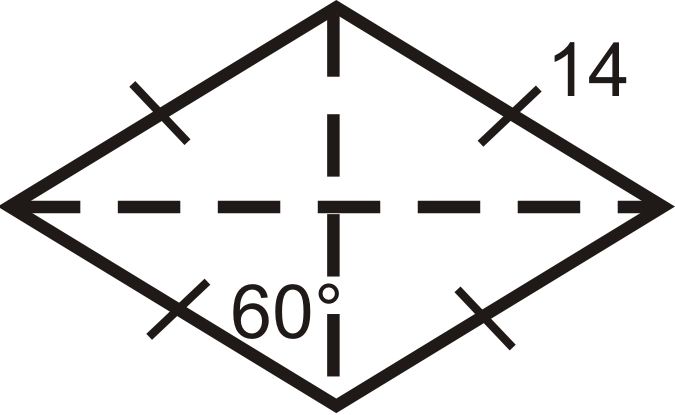
Solución
En un rombo, los cuatro triángulos creados por las diagonales son congruentes.
Aquí, cada triángulo es un triángulo 30-60-90 con una hipotenusa de 14. De las relaciones especiales del triángulo rectángulo la pierna corta es 7 y la pierna larga es\(7\sqrt{3}\).
\(P=4\cdot 14=56 units \qquad A=12\cdot 14\cdot 14\sqrt{3}=98\sqrt{3} units^2\)
Ejemplo\(\PageIndex{5}\)
Los vértices de un cuadrilátero son\(A(2,8),B(7,9),C(11,2),\: and\: D(3,3)\). Show\(ABCD\) es una cometa y encuentra su área.
Solución
Después de trazar los puntos, parece una cometa. \(AB=AD\)y\(BC=DC\). Las diagonales son perpendiculares si las pendientes son recíprocas negativas entre sí.
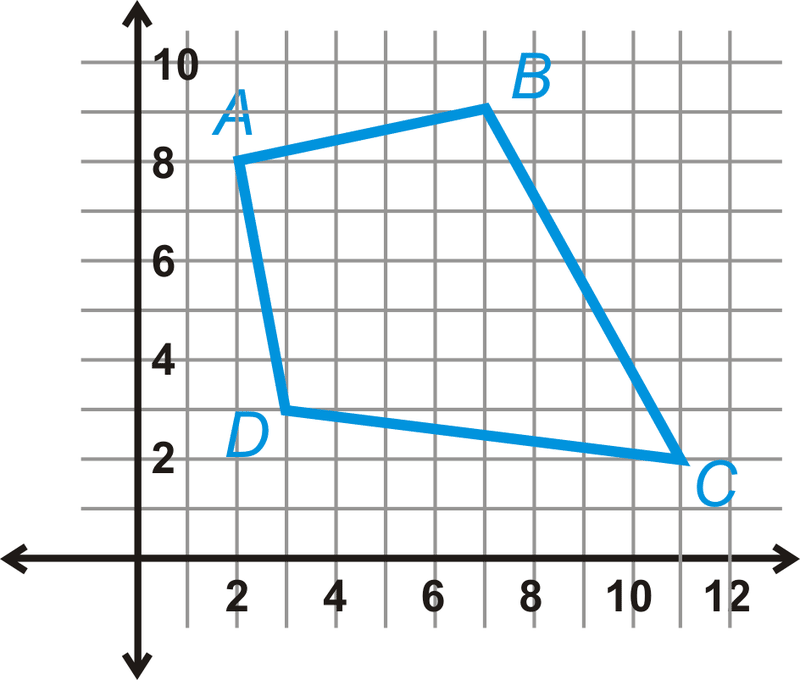
\(m_{AC}=\dfrac{2−8}{11−2}=−\dfrac{6}{9}=−\dfrac{2}{3}\)
\(m_{BD}=9−37−3=64=32\)
Las diagonales son perpendiculares, así\(ABCD\) es una cometa. Para encontrar el área, necesitamos encontrar la longitud de las diagonales,\(AC\) y\(BD\).
\(d_1=\sqrt{(2−11)^2+(8−2)^2}\)
\(=\sqrt{(−9)^2+6^2}\)
\(=\sqrt{81+36=\sqrt{117}=3\sqrt{13}\)
\(d_2=\sqrt{(7−3)^2+(9−3)^2}\)
\(=\sqrt{4^2+6^2}\)
\(=\sqrt{16+36}=\sqrt{52}=2\sqrt{13}\)
Enchufe estas longitudes en la fórmula de área para una cometa. \(A=12(3\sqrt{13})(2\sqrt{13})=39 units^2\)
Revisar
- ¿Crees que todos los rombos y cometas con las mismas longitudes diagonales tienen la misma área? Explica tu respuesta.
Encuentra el área de las siguientes formas. Redondea tus respuestas a la centésima más cercana.
-
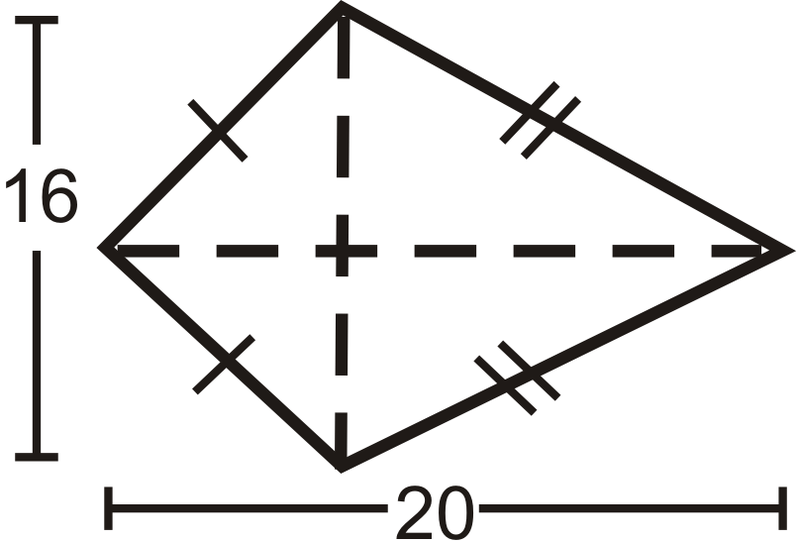
Figura\(\PageIndex{9}\) -
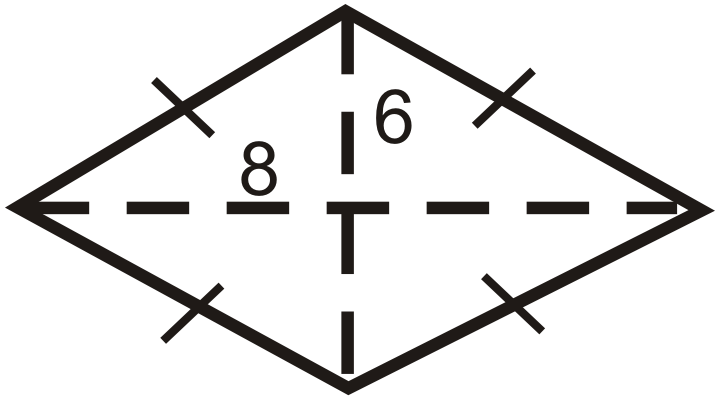
Figura\(\PageIndex{10}\) -
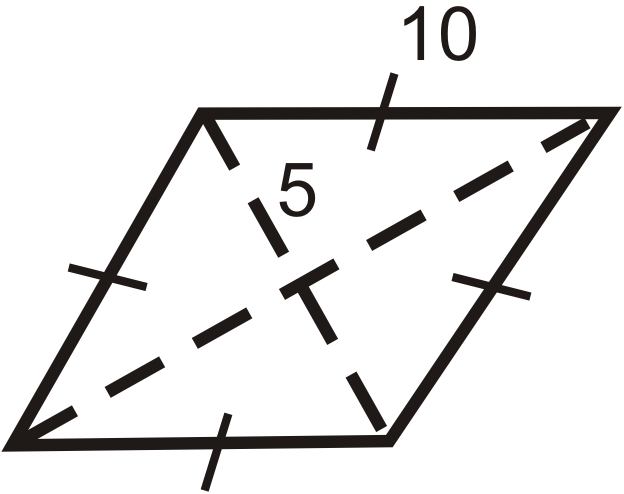
Figura\(\PageIndex{11}\) -
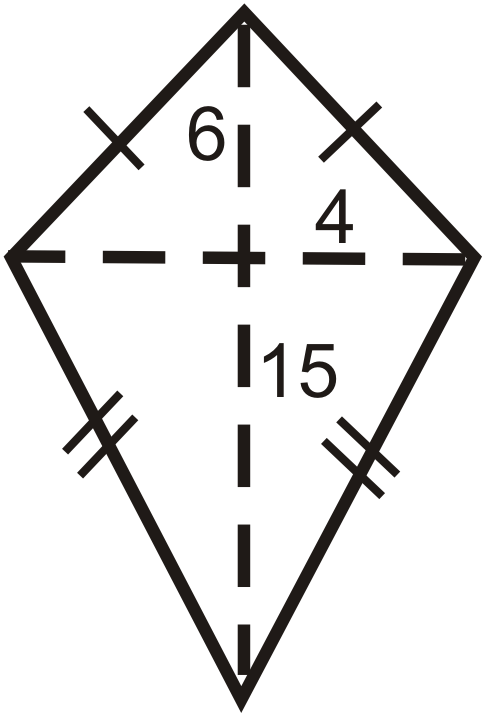
Figura\(\PageIndex{12}\) -
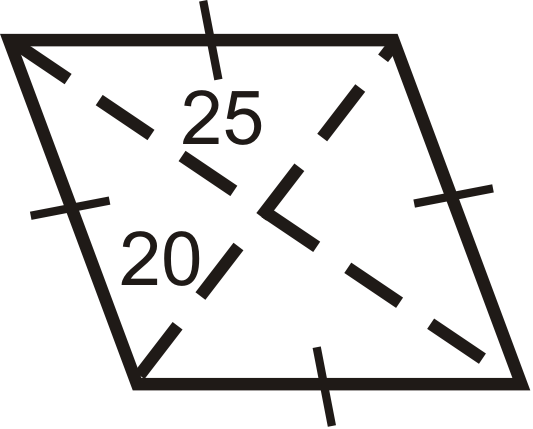
Figura\(\PageIndex{13}\) -
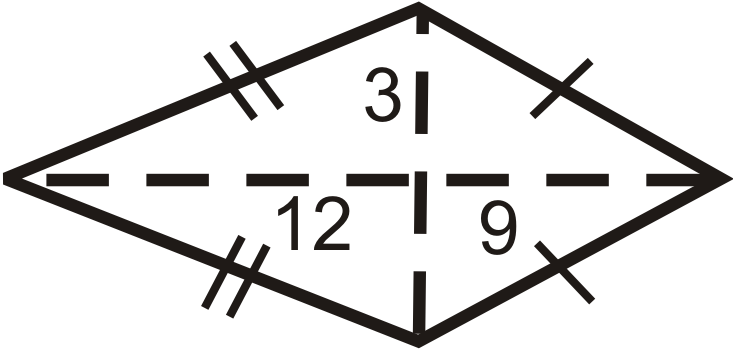
Figura\(\PageIndex{14}\)
Encuentra el área y perímetro de las siguientes formas. Redondea tus respuestas a la centésima más cercana.
-
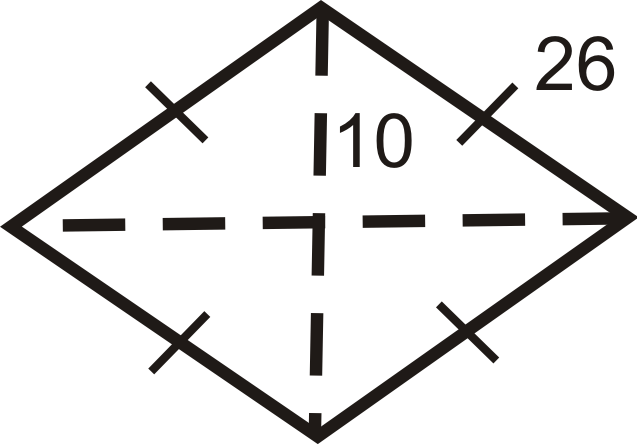
Figura\(\PageIndex{15}\) -
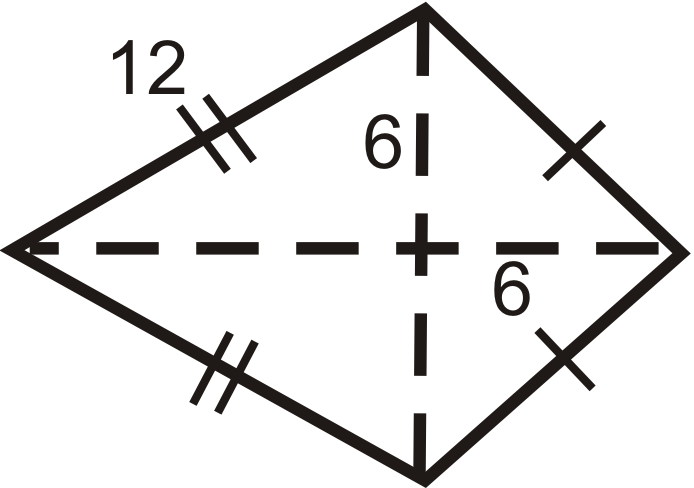
Figura\(\PageIndex{16}\) -
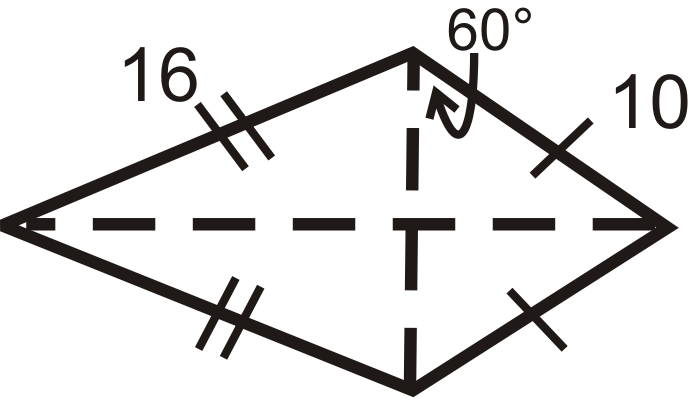
Figura\(\PageIndex{17}\) -
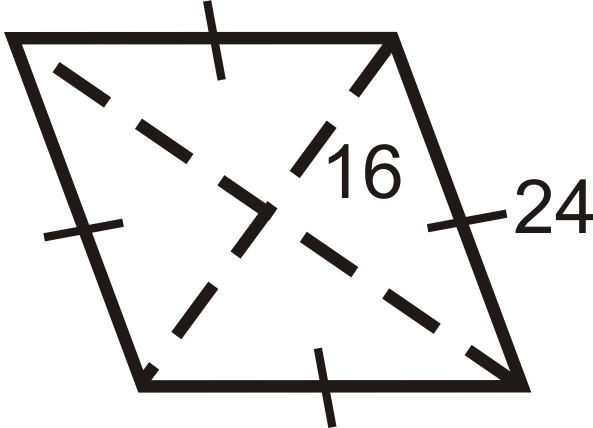
Figura\(\PageIndex{18}\)
Para las preguntas 12 y 13, el área de un rombo es\(32\: units^2\).
- ¿Cuál tendría que ser el producto de las diagonales para que fuera la zona\(32 units^2\)?
- Enumere dos posibilidades para la longitud de las diagonales, en función de su respuesta de #12.
Para las preguntas 14 y 15, el área de una cometa es\(54\: units^2\).
- ¿Cuál tendría que ser el producto de las diagonales para que fuera la zona\(54\: units^2\)?
- Enumere dos posibilidades para la longitud de las diagonales, en función de su respuesta de #14.
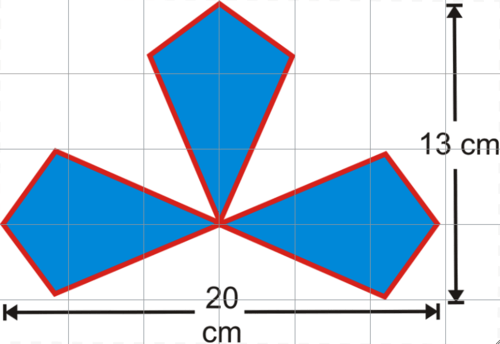
Sherry diseñó el logo para una nueva compañía, conformada por 3 cometas congruentes.
- ¿Cuáles son las longitudes de las diagonales para una cometa?
- Encuentra el área de una cometa.
- Encuentra el área de todo el logo.
El vocabulario
| Término | Definición |
|---|---|
| zona | La cantidad de espacio dentro de una figura. El área se mide en unidades cuadradas. |
| cometa | Un cuadrilátero con distintos lados congruentes adyacentes. |
| perímetro | La distancia alrededor de una forma. El perímetro de cualquier figura debe tener una unidad de medida adherida al mismo. Si no se dan unidades específicas (pies, pulgadas, centímetros, etc), escriba unidades. |
| Congruente | Las figuras congruentes son idénticas en tamaño, forma y medida. |
| Patas de un Triángulo Recto | Las patas de un triángulo rectángulo son los dos lados más cortos del triángulo rectángulo. Las patas están adyacentes al ángulo recto. |
Recursos adicionales
Elemento Interactivo
Video: Área y Perímetro de Rombos y Cometas Principios - Básico
Actividades: Área y Perímetro de Rombos y Cometas Preguntas de Discusión
Ayudas de estudio: Guía de estudio de triángulos y cuadriláteros
Práctica: Área y Perímetro de Rombos y Cometas
Mundo Real: Perímetro