5.16: Cometas
- Page ID
- 107504
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\(\newcommand{\longvect}{\overrightarrow}\)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Cuadriláteros con dos conjuntos distintos de lados adyacentes y congruentes.
Una cometa es un cuadrilátero con dos conjuntos distintos de lados congruentes adyacentes. Parece una cometa que vuela en el aire.

A partir de la definición, una cometa podría ser cóncava. Si una cometa es cóncava, se llama dardo. La palabra distinto en la definición significa que los dos pares de lados congruentes tienen que ser diferentes. Esto significa que un cuadrado o un rombo no es una cometa.
Los ángulos entre los lados congruentes se denominan ángulos de vértice. Los otros ángulos se llaman ángulos no vértices. Si dibujamos la diagonal a través de los ángulos de vértice, tendríamos dos triángulos congruentes.
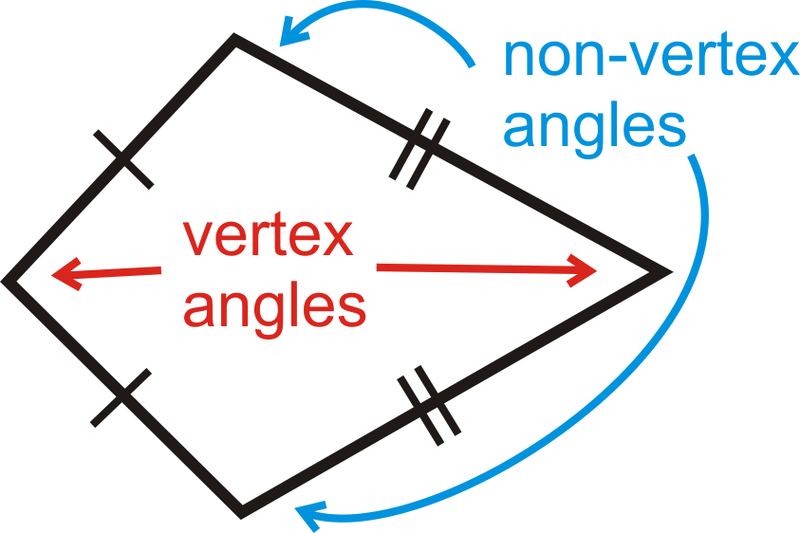
Datos sobre las cometas
1. Los ángulos que no son vértices de una cometa son congruentes.
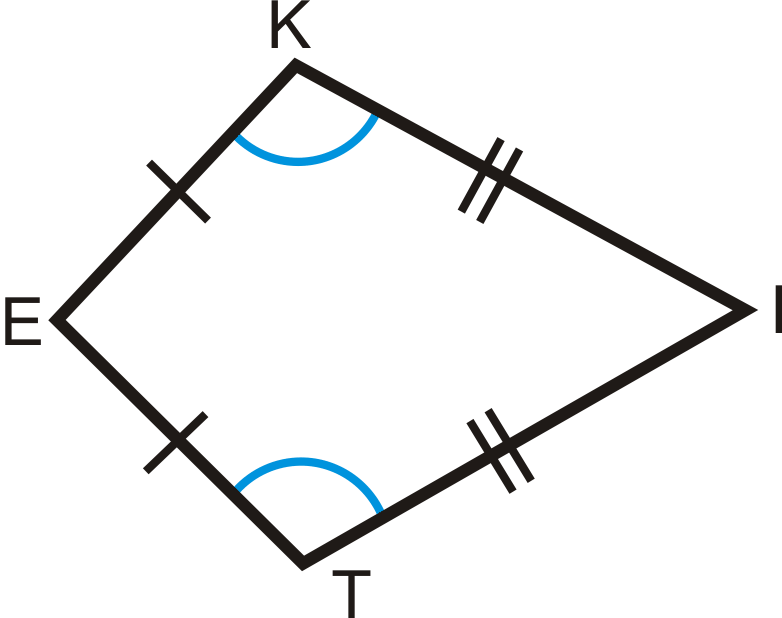
Si\(KITE\) es una cometa, entonces\(\angle K\cong \angle T\).
2. La diagonal a través de los ángulos de vértice es el ángulo bisectriz para ambos ángulos.

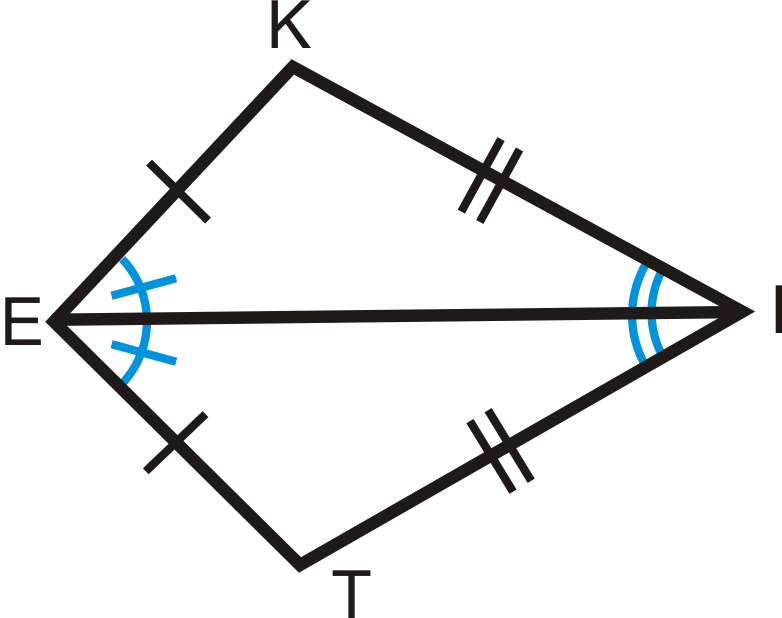 Figura\(\PageIndex{4}\)
Figura\(\PageIndex{4}\)Si\(KITE\) es una cometa, entonces\(\angle KEI\cong \angle IET\) y\(\angle KIE\cong \angle EIT\).
3. Teorema de las Diagonales de Cometas: Las diagonales de una cometa son perpendiculares.
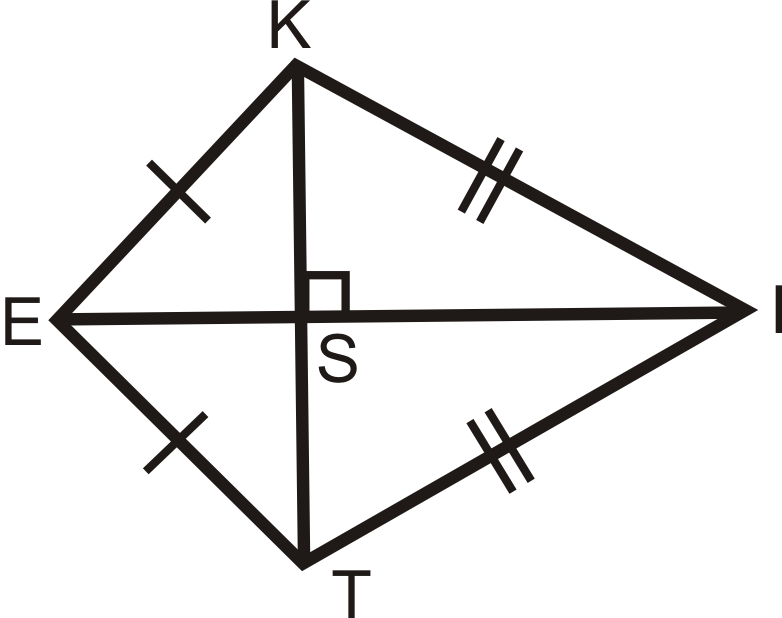 Figura\(\PageIndex{5}\)
Figura\(\PageIndex{5}\)\( \Delta KET\)y\(\Delta KIT\) son triángulos isósceles, así\(\overline{EI}\) es la bisectriz perpendicular de\(\overline{KT}\) (Teorema del Triángulo Isósceles).
¿Y si te dijeran que\(WIND\) es una cometa y te den información sobre algunos de sus ángulos o sus diagonales? ¿Cómo encontrarías la medida de sus otros ángulos o sus lados?
Para los Ejemplos 1 y 2, utilice la siguiente información:
\(KITE\)es una cometa.
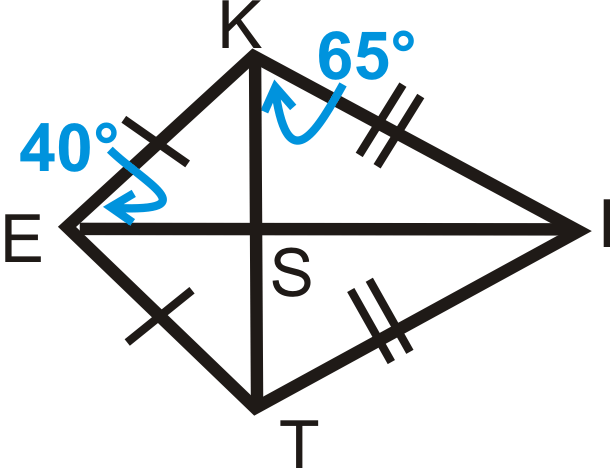
Ejemplo\(\PageIndex{1}\)
Encuentra\(m\angle KIS\).
Solución
\(m\angle KIS=25^{\circ}\)por el Teorema de la Suma del Triángulo (recuerde que\ ángulo KSI es un ángulo recto porque las diagonales son perpendiculares.)
Ejemplo\(\PageIndex{2}\)
Encuentra\(m\angle IST\).
Solución
\(m\angle IST=90^{\circ}\)porque las diagonales son perpendiculares.
Ejemplo\(\PageIndex{3}\)
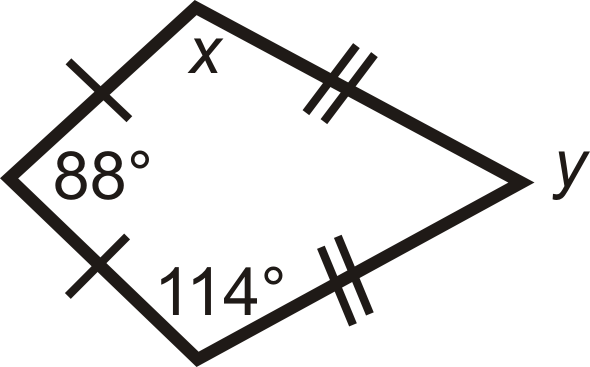
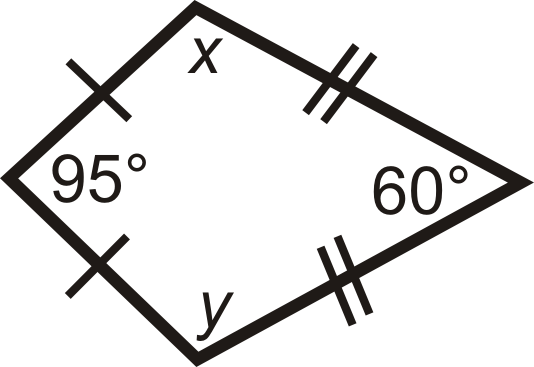
Encuentra las medidas faltantes en las cometas a continuación.
-
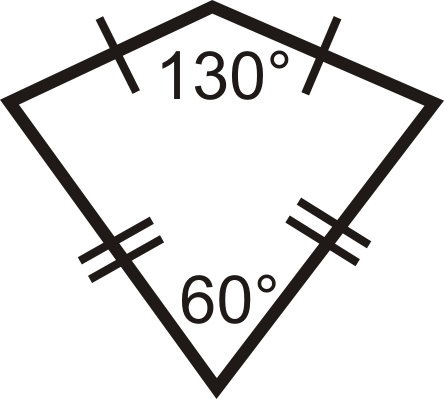
Figura\(\PageIndex{7}\) -
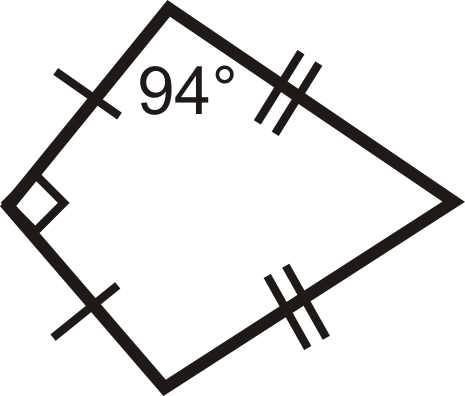
Figura\(\PageIndex{8}\)
Solución
- Los dos ángulos que quedan son los ángulos que no son vértices, los cuales son congruentes.
\( \begin{aligned} 130^{\circ} +60^{\circ} +x+x=360^{\circ} \\ 2x&=170^{\circ} \\ x&=85^{\circ} \qquad Both angles are 85^{\circ} \end{aligned}\)
- El otro ángulo no vértice también lo es\(94^{\circ}\). Para encontrar el cuarto ángulo, restar los otros tres ángulos de\(360^{\circ}\).
\(\begin{aligned} 90^{\circ} +94^{\circ} +94^{\circ} +x &=360^{\circ} \\ x&=82^{\circ} \end{aligned}\)
Ejemplo\(\PageIndex{4}\)
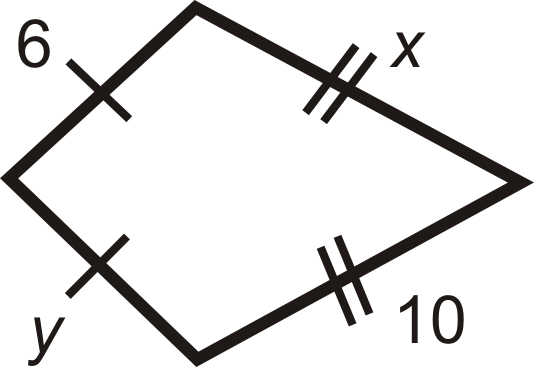
Usa el Teorema de Pitágoras para encontrar las longitudes de los lados de la cometa.
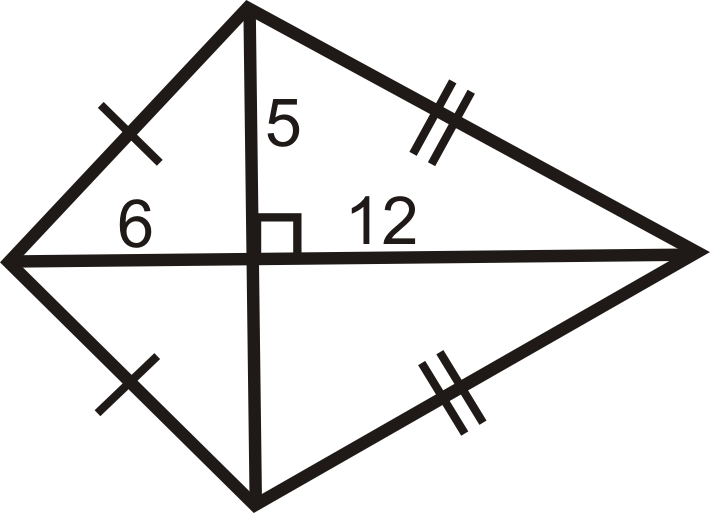
Solución
Recordemos que dice el Teorema de Pitágoras\(a^2+b^2=c^2\), donde\(c\) está la hipotenusa. En esta cometa, los costados son las hipotenusas.
\ (\ begin {array} {rr}
6^ {2} +5^ {2} =h^ {2} & 12^ {2} +5^ {2} =j^ {2}\\
36+25=h^ {2} & 144+25=j^ {2}\
61=h^ {2} & 169=j^ {2}\
\ sqrt {61} =h & 13=j
\ end {array}\)
Ejemplo\(\PageIndex{5}\)
Demostrar que los ángulos no vértices de una cometa son congruentes.
Dado:\(KITE\) con\(\overline{KE}\cong \overline{TE}\) y\(\overline{KI}\cong \overline{TI}\)
Demostrar:\(\angle K\cong \angle T\)
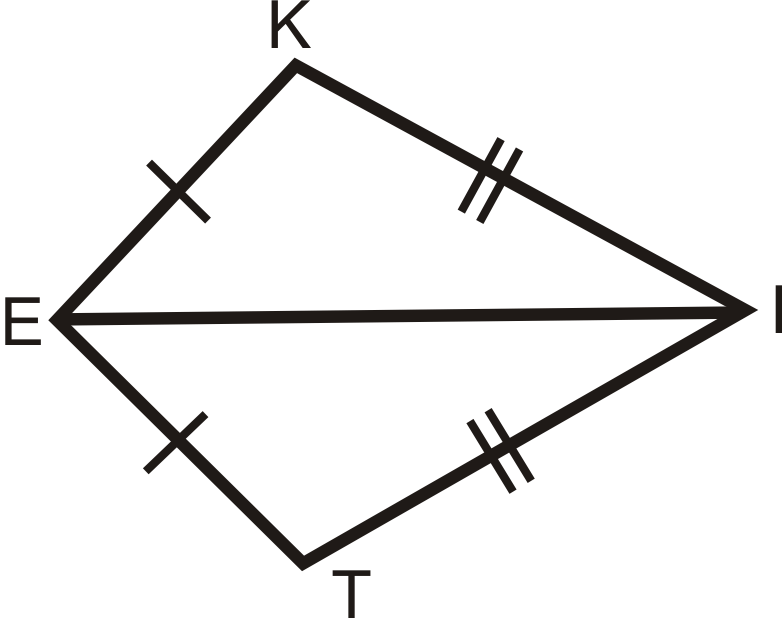
Solución
| Declaración | Razón |
|---|---|
| 1. \(\overline{KE}\cong \overline{TE}\)y\(\overline{KI}\cong \overline{TI}\) | 1. Dado |
| 2. \( \overline{EI}\cong \overline{EI}\) | 2. PoC reflexivo |
| 3. \(\Delta EKI\cong \Delta ETI\) | 3. SSS |
| 4. \(\angle K\cong \angle T\) | 4. CPCTC |
Revisar
Para las preguntas 1-6, encuentre el valor de las variables faltantes. Todas las figuras son cometas.
-
Figura\(\PageIndex{11}\) -
Figura\(\PageIndex{12}\) -
Figura\(\PageIndex{13}\) -
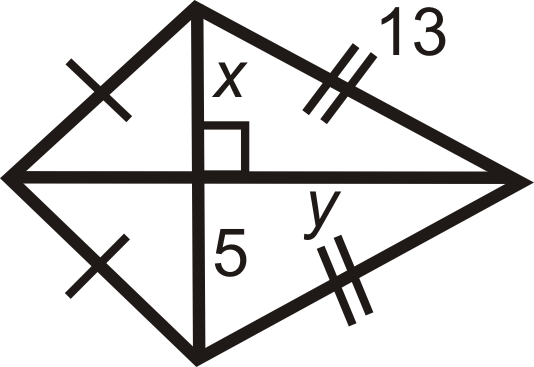
Figura\(\PageIndex{14}\) -
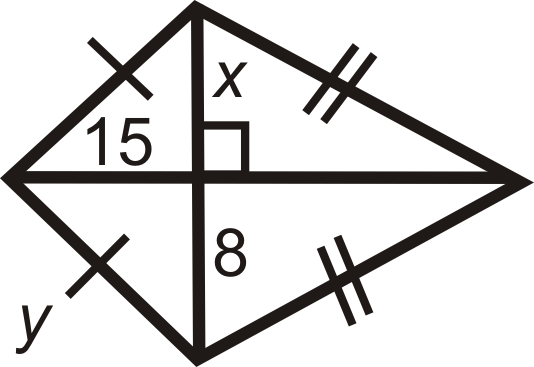 Figura\(\PageIndex{15}\)
Figura\(\PageIndex{15}\) -
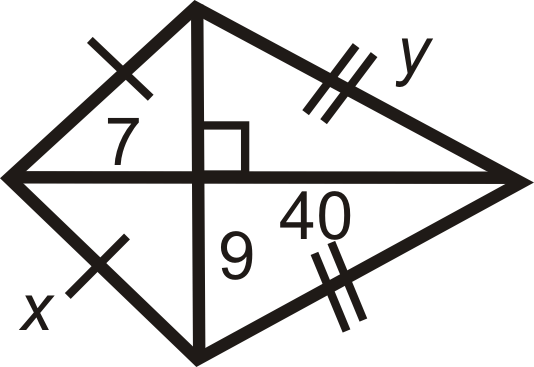
Figura\(\PageIndex{16}\)
Para las preguntas 7-11, encuentre el valor de las variables faltantes.
-
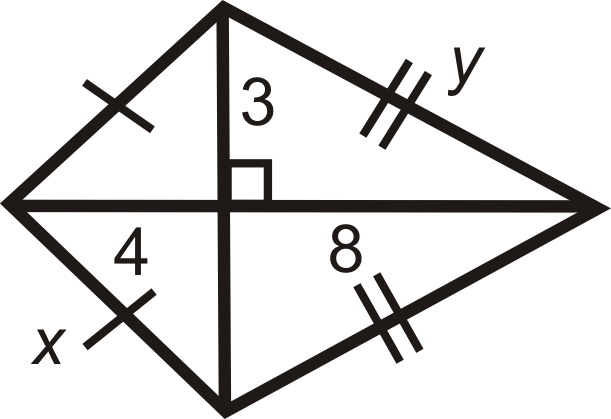
Figura\(\PageIndex{17}\) -
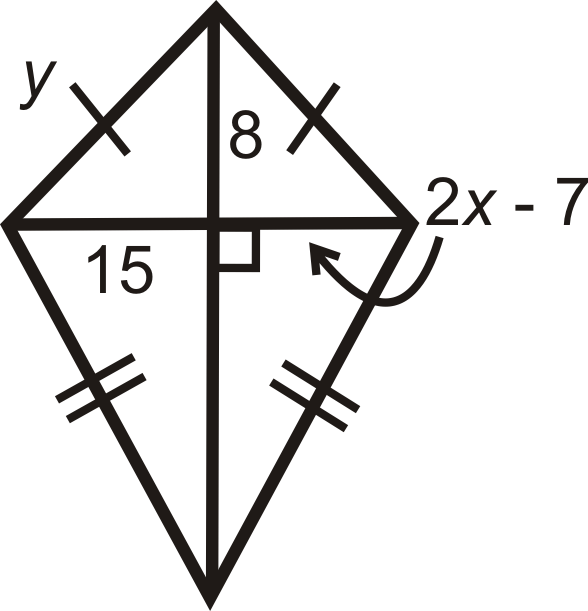
Figura\(\PageIndex{18}\) -
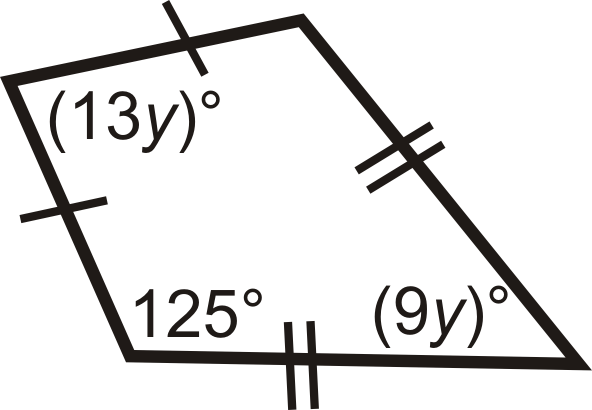
Figura\(\PageIndex{19}\) -
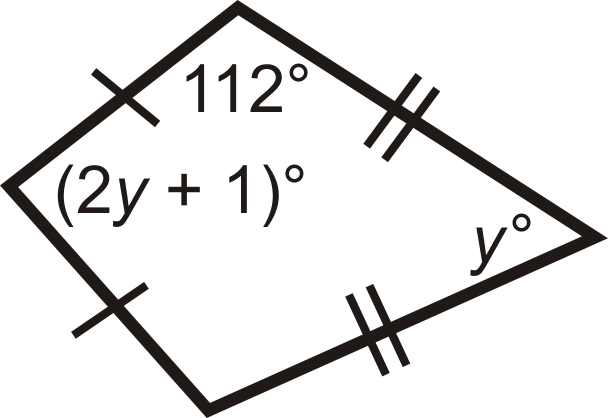
Figura\(\PageIndex{20}\) -
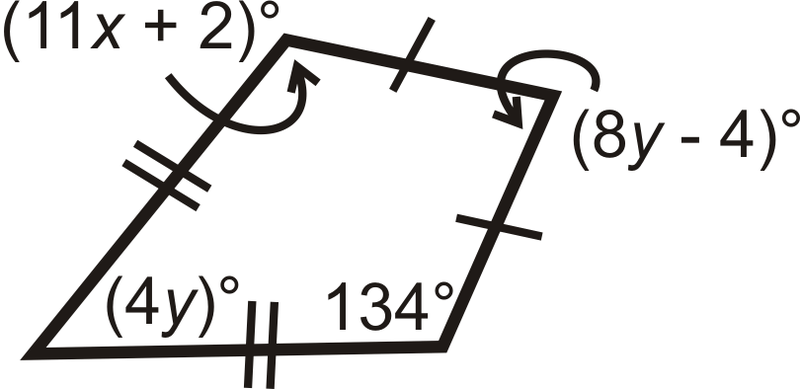
Figura\(\PageIndex{21}\)
- Rellene los espacios en blanco al comprobante a continuación.
Dado:\(\overline{KE}\cong \overline{TE}\) y\(\overline{KI}\cong \overline{TI}\)
Demostrar:\(\overline{EI}\) es el ángulo bisectriz de\(\angle KET\) y\(\angle KIT\)

| Declaración | Razón |
|---|---|
| 1. \( \overline{KE}\cong \overline{TE} and \overline{KI}\cong \overline{TI}\) | 1. |
| 2. \(\overline{EI}\cong \overline{EI}\) | 2. |
| 3. \(\Delta EKI\cong \Delta ETI\) | 3. |
| 4. | 4. CPCTC |
| 5. \(\overline{EI} is the angle bisector of \angle KET\)y\ ángulo KIT\) | 5. |
- Rellene los espacios en blanco al comprobante a continuación.
Dado:\(\overline{EK}\cong \overline{ET},\: \overline{KI}\cong \overline{IT}\)
Demostrar:\(\overline{KT}\perp \overline{EI}\)

| Declaración | Razón |
|---|---|
| 1. \(\overline{KE}\cong \overline{TE}\)y\(\overline{KI}\cong \overline{TI}\) | 1. |
| 2. | 2. Definición de triángulos isósceles |
| 3. \(\overline{EI}\)es el ángulo bisectriz de\(\angle KET\) y\(\angle KIT\) | 3. |
| 4. | 4. Teorema del Triángulo Isósceles |
| 5. \(\overline{KT}\perp \overline{EI}\) | 5. |
Reseña (Respuestas)
Para ver las respuestas de Revisar, abra este archivo PDF y busque la sección 6.7.
El vocabulario
| Término | Definición |
|---|---|
| cometa | Un cuadrilátero con distintos lados congruentes adyacentes. |
| Teorema de suma de triángulo | El Teorema de la Suma del Triángulo establece que los tres ángulos interiores de cualquier triángulo suman 180 grados. |
| Ángulos Verticales | Los ángulos verticales son un par de ángulos opuestos creados por líneas que se cruzan. |
Recursos adicionales
Elemento Interactivo
Video: Principios de Cometas - Básicos
Actividades: Cometas Preguntas de Discusión
Ayudas de estudio: Guía de estudio de trapecios y cometas
Práctica: Cometas
Mundo real: vete a volar una cometa

