5.19: Clasificación cuadrilátero en el plano de coordenadas
- Page ID
- 107495
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Identificar y calcular el área de las formas en base a las coordenadas de un plano.
Clasificación cuadrilátero
¿Y si te dieran un cuadrilátero en el plano de coordenadas? ¿Cómo podrías determinar si ese cuadrilátero califica como uno de los cuadriláteros especiales: paralelogramos, cuadrados, rectángulos, rombos, cometas o trapecios?
Al trabajar en el plano de coordenadas, a veces querrás saber qué tipo de forma es una forma determinada. Se debería poder decir fácilmente que es un cuadrilátero si tiene cuatro lados. Pero, ¿cómo puedes clasificarlo más allá de eso?
Primero debes graficar la forma si aún no se ha graficado. Mírala y mira si se parece a algún cuadrilátero especial. ¿Los lados parecen ser congruentes? ¿Se encuentran en ángulo recto? Esto te dará un lugar para comenzar.
Una vez que tienes una conjetura de qué tipo de cuadrilátero es, tu trabajo es probar tu suposición. Para demostrar que un cuadrilátero es un paralelogramo, rectángulo, rombo, cuadrado, cometa o trapecio, debes demostrar que cumple con la definición de esa forma O que tiene propiedades que solo esa forma tiene.
Si resulta que tu conjetura estuvo equivocada porque la forma no cumple con las propiedades necesarias, puedes volver a adivinar. Si no parece ser ningún tipo de cuadrilátero especial entonces es simplemente un cuadrilátero.
Los ejemplos a continuación te ayudarán a ver cómo podría ser este proceso.
Clasificación de paralelogramos
Determinar qué tipo de paralelogramo es Tune:\(T(0,10),\: U(4,2),\: N(−2,−1),\: and\: E(−6,7)\).
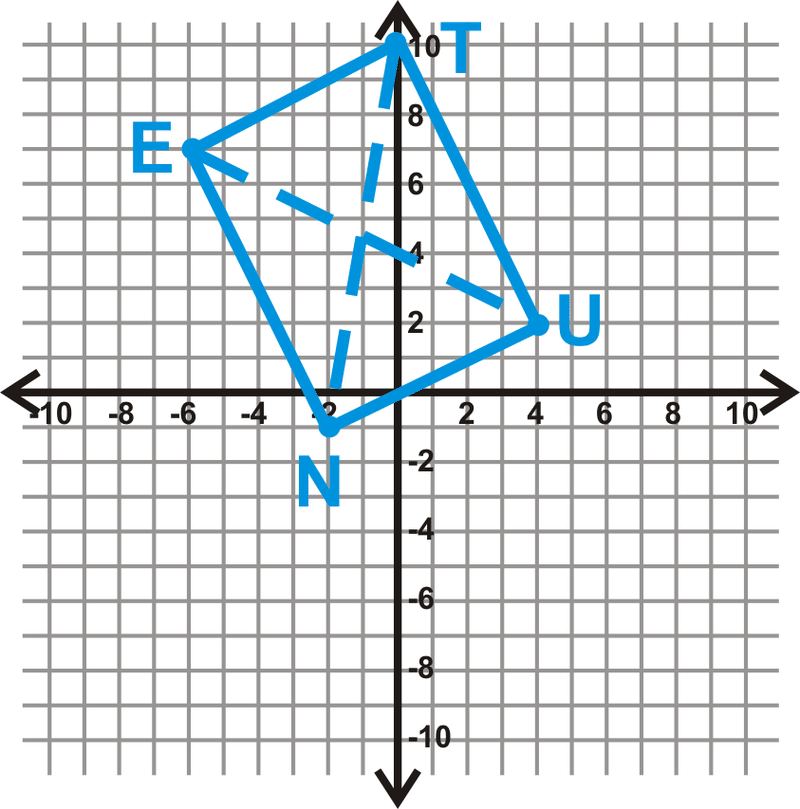
Esto parece un rectángulo. Veamos si las diagonales son iguales. Si lo son, entonces TUNE es un rectángulo.
\ (\ begin {alineado}
E U &=\ sqrt {(-6-4) ^ {2} + (7-2) ^ {2}} & T N &=\ sqrt {(0+2) ^ {2} + (10+1) ^ {2}}\\
&=\ sqrt {(-10) ^ {2} +5^ {2}} & &=\ sqrt {2^ {2}} +11^ {2}}\\
&=\ sqrt {100+25} & &=\ sqrt {4+121}\\
&=\ sqrt {125} & &=\ sqrt {125}
\ end {alineado}\)
Si las diagonales también son perpendiculares, entonces\(TUNE\) es un cuadrado.
\(\text { Slope of } E U=\dfrac{7-2}{-6-4}=-\dfrac{5}{10}=-\dfrac{1}{2} \quad \text { Slope of } T N=\dfrac{10-(-1)}{0-(-2)}=\dfrac{11}{2}\)
La pendiente de\(EU\)\(\neq\) pendiente de\(TN\), así\(TUNE\) es un rectángulo.
Determinar si un cuadrilátero es un paralelogramo
Un cuadrilátero se define por las cuatro líneas\(y=2x+1\),\(y=−x+5\),\(y=2x−4\), y\(y=−x−5\). ¿Este cuadrilátero es un paralelogramo?
Para comprobar si es un paralelogramo tenemos que comprobar que tiene dos pares de lados paralelos. De las ecuaciones podemos ver que las pendientes de las líneas son 2, −1, 2 y −1. Debido a que dos pares de pendientes coinciden, esta forma tiene dos pares de lados paralelos y es un paralelogramo.
Determinación de Tipos de Cuadriláteros
Determinar qué tipo de cuadrilátero\(RSTV\) es. Simplifica todos los radicales.
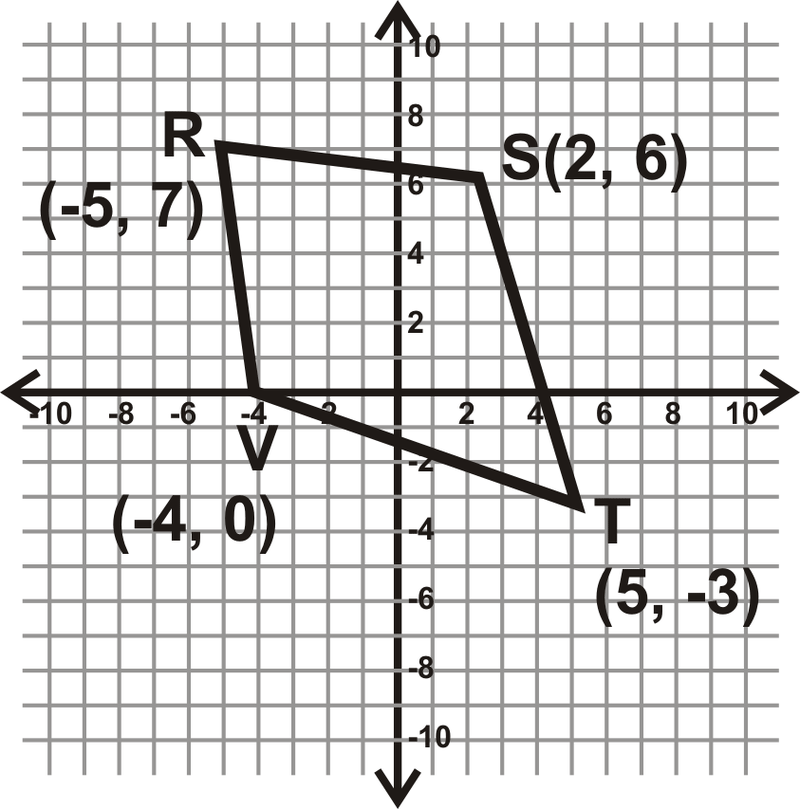
Hay dos direcciones que podrías tomar aquí. Primero, podrías determinar si las diagonales se bisectan entre sí. Si lo hacen, entonces es un paralelogramo. O bien, podrías encontrar los largos de todos los lados. Hagamos esta opción.
\ (\ begin {alineado}
R S &=\ sqrt {(-5-2) ^ {2} + (7-6) ^ {2}} & S T &=\ sqrt {(2-5) ^ {2} + (6- (-3)) ^ {2}}\\
&=\ sqrt {(-7) ^ {2} +1 ^ {2}} & & =\ sqrt {(-3) ^ {2} +9^ {2}}\\
&=\ sqrt {50} =5\ sqrt {2} & &=\ sqrt {90} =3\ sqrt {10}\\
R V=&\ sqrt {(-5- (-4)) ^ {2} + (7-0) ^ {2}} & V T &=\ sqrt {(-4-5) ^ {2} + (0- (-3)) ^ {2}}\\
=&\ sqrt {(-1) ^ {2} +7^ {2}} & &=\ sqrt {(-9) ^ {2} +3^ {2}}\
=&\ sqrt {50} =5\ sqrt {2} & &=\ sqrt {90} =3\ sqrt {10}
\ end {alineado}\)
De esto vemos que los lados adyacentes son congruentes. Por lo tanto,\(RSTV\) es una cometa.
Elemento Interactivo
Agrega el texto del elemento interactivo aquí. Esta caja NO se imprimirá en pdf
Revisión de álgebra: Cuando se le pide que “simplifique el radical”, saque todos los números cuadrados (1, 4, 9, 16, 25,...) del radical. Arriba\(\sqrt{50}=\sqrt{25\cdot 2}\). Sabemos\(\sqrt{25}=5\), entonces\(\sqrt{50}=\sqrt{25\cdot 2}=5\sqrt{2}\).
Reconocer paralelogramos
¿El cuadrilátero es\(ABCD\) un paralelogramo?
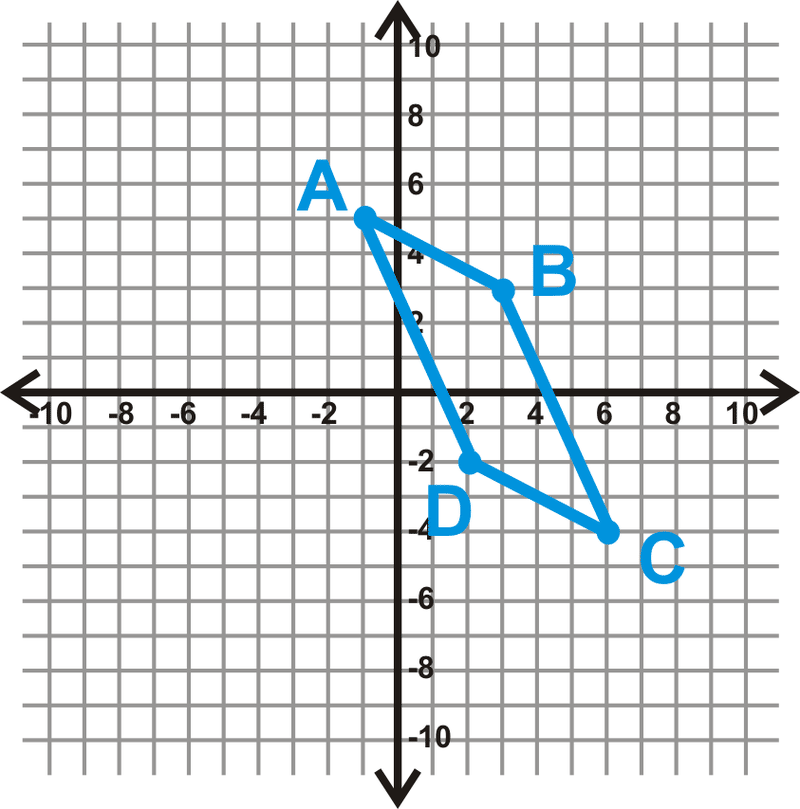
Hemos determinado que hay cuatro formas diferentes de mostrar un cuadrilátero es un paralelogramo en el\(x−y\) plano. Comprobemos si un par de lados opuestos son congruentes y paralelos. Primero, encuentra la longitud de\(AB\) y\(CD\).
\ (\ begin {alineado}
A B &=\ sqrt {(-1-3) ^ {2} + (5-3) ^ {2}} & C D &=\ sqrt {(2-6) ^ {2} + (-2+4) ^ {2}}\\
&=\ sqrt {(-4) ^ {2} +2^ {2}} & & =\ sqrt {() -4 ^ {2} +2^ {2}}\\
&=\ sqrt {16+4} & &=\ sqrt {16+4}\\
&=\ sqrt {20} & &=\ sqrt {20}
\ end {alineado}\)
\(AB=CD\), por lo que si las dos líneas tienen la misma pendiente,\(ABCD\) es un paralelogramo.
\(\text { Slope } A B=\dfrac{5-3}{-1-3}=\dfrac{2}{-4}=-\dfrac{1}{2} \text { Slope } C D=\dfrac{-2+4}{2-6}=\dfrac{2}{-4}=-\dfrac{1}{2}\)
Por lo tanto,\(ABCD\) es un paralelogramo.
Ejemplo\(\PageIndex{1}\)
Un cuadrilátero se define por las cuatro líneas\(y=2x+1\),\(y=−2x+5\),\(y=2x−4\), y\(y=−2x−5\). ¿Este cuadrilátero es un rectángulo?
Solución
Para ser un rectángulo una forma debe tener cuatro ángulos rectos. Esto quiere decir que los lados deben ser perpendiculares entre sí. De las ecuaciones dadas vemos que las pendientes son 2, −2, 2 y −2. Debido a que las pendientes no son recíprocas opuestas entre sí, los lados no son perpendiculares, y la forma no es un rectángulo.
Ejemplo\(\PageIndex{2}\)
Determinar qué tipo de cuadrilátero\(ABCD\) es. \(A(−3,3),\: B(1,5),\: C(4,−1),\: D(1,−5)\). Simplifica todos los radicales.
Solución
Primero, grafica\(ABCD\). Esto hará que sea más fácil averiguar qué tipo de cuadrilátero es. De la gráfica, podemos decir que esto no es un paralelogramo. Encuentra la pendiente de\ overline {BC} y\ overline {AD} para ver si son paralelas.
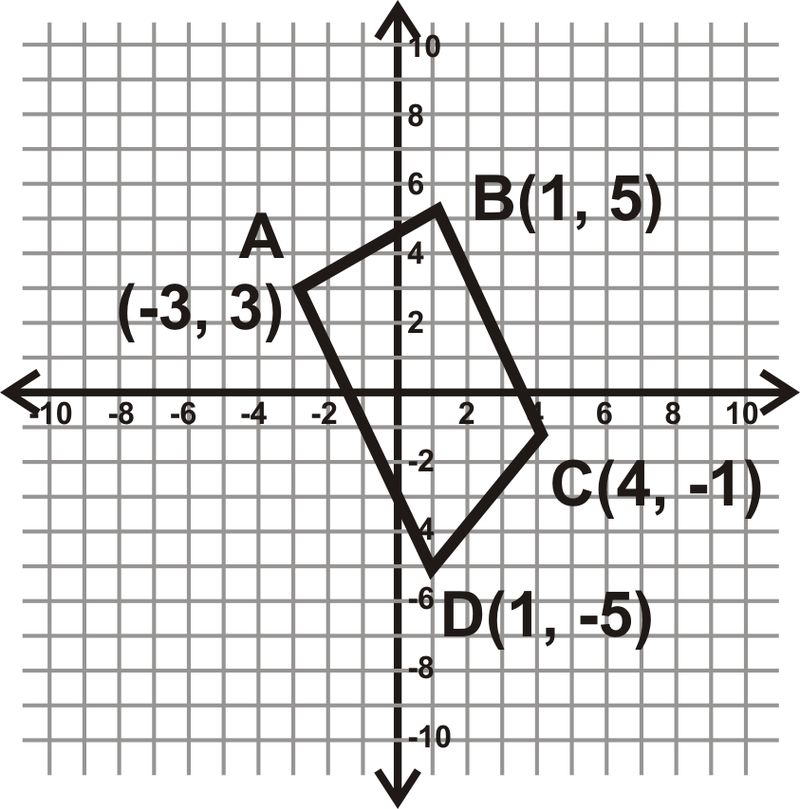
\ (\ begin {array} {l}
\ text {Pendiente de}\ overline {B C} =\ dfrac {5- (-1)} {1-4} =\ dfrac {6} {-3} =-2\
\ texto {Pendiente de}\ overline {A D} =\ dfrac {3- (-5)} {-3-1} =\ dfrac {8} {-4} = -2
\ end {array}\)
Ahora sabemos\(\overline{BC} \parallel \overline{AD}\). Se trata de un trapecio. Para determinar si es un trapecio isósceles, encontrar\(AB\) y\(CD\).
\ (\ begin {alineado}
A B &=\ sqrt {(-3-1) ^ {2} + (3-5) ^ {2}} & S T &=\ sqrt {(4-1) ^ {2} + (-1- (-5)) ^ {2}}\\
&=\ sqrt {(-4) ^ {2} + (-2) ^ {2}} & &=\ sqrt {3^ {2} +4^ {2}}\\
&=\ sqrt {20} =2\ sqrt {5} & &=\ sqrt {25} =5
\ end {alineado}\)
\(AB\neq CD\), por lo tanto esto es sólo un trapecio.
Ejemplo\(\PageIndex{3}\)
Determinar qué tipo de cuadrilátero\(EFGH\) es. \(E(5,−1),\: F(11,−3),\: G(5,−5),\: H(−1,−3)\)
Solución
No vamos a graficar este ejemplo. Encontremos la longitud de los cuatro lados.
\ (\ begin {alineado}
E F &=\ sqrt {(5-11) ^ {2} + (-1- (-3)) ^ {2}} & F G &=\ sqrt {(11-5) ^ {2} + (-3- (-5)) ^ {2}}\\
&=\ sqrt {(-6) ^ {2} +2^ {2}} &=&\ sqrt {6^ {2} +2^ {2}}\\
&=\ sqrt {40} =2\ sqrt {10} & &=\ sqrt {40} =2\ sqrt {10}\\
G H &=\ sqrt { (5- (-1)) ^ {2} + (-5- (-3)) ^ {2}} & H &=\ sqrt {(-1-5) ^ {2} + (-3- (-1)) ^ {2}}\\
&=\ sqrt {6^ {2} + (-2) ^ {2}} & &=\ sqrt {(-6) ^ {2} + (-2) ^ {2} + (-2) ^ {2} {2}}\\
=&\ sqrt {40} =2\ sqrt {10} & &=\ sqrt {40} =2\ sqrt {10}
\ end {alineado}\)
Los cuatro lados son iguales. Es decir, este cuadrilátero es un rombo o un cuadrado. La diferencia entre ambos es que un cuadrado tiene cuatro ángulos de 90° y diagonales congruentes. Encontremos la longitud de las diagonales.
\ (\ begin {alineado}
E G &=\ sqrt {(5-5) ^ {2} + (-1- (-5)) ^ {2}} & F H &=\ sqrt {(11- (-1)) ^ {2} + (-3- (-3)) ^ {2}}\\
&=\ sqrt {0^ {2} +4^ {2}} & =\ sqrt rt {12^ {2} +0^ {2}}\\
&=\ sqrt {16} =4 & &=\ sqrt {144} =12
\ end {alineado}\)
Las diagonales no son congruentes, así\(EFGH\) es un rombo.
Revisar
- Si un cuadrilátero tiene exactamente un par de lados paralelos, ¿qué tipo de cuadrilátero es?
- Si un cuadrilátero tiene dos pares de lados paralelos y uno en ángulo recto, ¿qué tipo de cuadrilátero es?
- Si un cuadrilátero tiene diagonales perpendiculares, ¿qué tipo de cuadrilátero es?
- Si un cuadrilátero tiene diagonales perpendiculares y congruentes, ¿qué tipo de cuadrilátero es?
- Si un cuadrilátero tiene cuatro lados congruentes y uno en ángulo recto, ¿qué tipo de cuadrilátero es?
Determinar qué tipo de cuadrilátero\(ABCD\) es.
- \(A(−2,4),\: B(−1,2),\: C(−3,1),\: D(−4,3)\)
- \(A(−2,3),\: B(3,4),\: C(2,−1),\: D(−3,−2)\)
- \(A(1,−1),\: B(7,1),\: C(8,−2),\: D(2,−4)\)
- \(A(10,4),\: B(8,−2),\: C(2,2),\: D(4,8)\)
- \(A(0,0),\: B(5,0),\: C(0,4),\: D(5,4)\)
- \(A(−1,0),\: B(0,1),\: C(1,0),\: D(0,−1)\)
- \(A(2,0),\: B(3,5),\: C(5,0),\: D(6,5)\)
SRUE es un rectángulo y PRUC es un cuadrado.
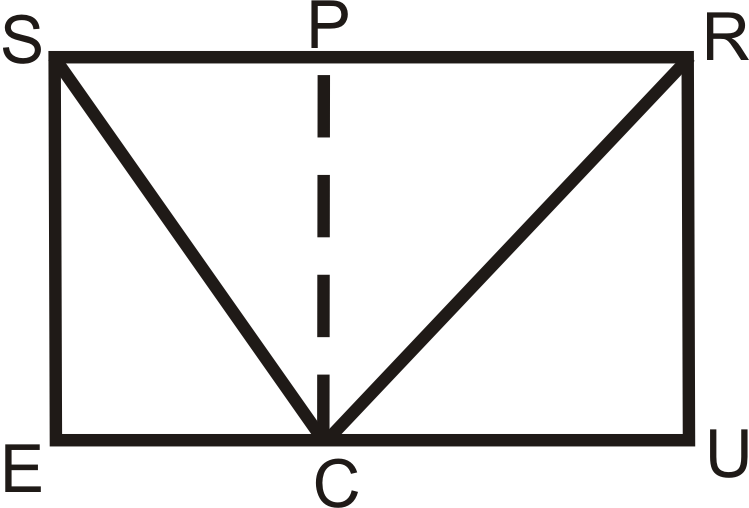
- ¿Qué tipo de cuadrilátero es\(SPCE\)?
- Si\(SR=20\) y\(RU=12\), encuentra\(CE\).
- Encuentra SC y RC con base en la información de la parte b. Redondea tus respuestas a la centésima más cercana.
Reseña (Respuestas)
Para ver las respuestas de Revisar, abra este archivo PDF y busque la sección 6.8.
vocabulario
| Término | Definición |
|---|---|
| Kite | Una cometa es un cuadrilátero con distintos lados congruentes adyacentes. |
| Paralelogramo | Un paralelogramo es un cuadrilátero con dos pares de lados paralelos. |
| Cuadrilátero | Un cuadrilátero es una figura cerrada con cuatro lados y cuatro vértices. |
| Rectángulo | Un rectángulo es un cuadrilátero con cuatro ángulos rectos. |
| Rombo | Un rombo es un cuadrilátero con cuatro lados congruentes. |
| Trapezoide | Un trapecio es un cuadrilátero con exactamente un par de lados opuestos paralelos. |

