5.20: Polígonos regulares e irregulares
- Page ID
- 107546
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\(\newcommand{\longvect}{\overrightarrow}\)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Comprender e identificar polígonos regulares e irregulares.

Logan ha estado rastreando señales de calles alrededor de su ciudad. Se prepara para trazar el letrero de la calle anterior. Él perfila la forma y dibuja los bordes redondos como líneas rectas. ¿La forma resultante será un polígono regular o irregular, y qué tipo de polígono será?
En este concepto, aprenderás a determinar si un polígono es regular o irregular.
Determinar si los Polígonos son Regulares o Irregulares
Un polígono puede tener un cierto número de lados, pero los lados no necesariamente tienen que ser de la misma longitud. Ambos polígonos de abajo son pentágonos porque ambos tienen cinco ángulos y lados, pero mira las diferencias.

En el primer pentágono, todos los ángulos son congruentes y todos los lados son congruentes. En el segundo pentágono, los ángulos tienen diferentes medidas y los lados tienen diferentes longitudes.
Un polígono regular tiene ángulos congruentes y lados congruentes . Cualquier polígono puede ser un polígono regular.
Mira los polígonos regulares a continuación.

Como puede ver, un hexágono regular tiene seis lados congruentes y seis ángulos congruentes. Un hexágono regular, por mucho que sean sus lados, siempre tendrá ángulos que midan\(120^{\circ}\).
Un octágono regular tiene ocho ángulos congruentes y ocho lados congruentes. Cada octágono regular tiene las mismas medidas de ángulo.
El término “rectángulo regular” no suele usarse porque un rectángulo con lados congruentes es en realidad un cuadrado. Los cuatro ángulos en un cuadrado son siempre\(90^{\circ}\), y su suma es siempre\(360^{\circ}\). Sin embargo, hay un nombre especial para un “triángulo regular”. Un triángulo con tres lados congruentes se llama triángulo equilátero. Sus tres ángulos son siempre\(60^{\circ}\), y su suma es siempre\(180^{\circ}\).
Cualquier polígono que no tenga todos los lados congruentes es un polígono irregular . Los polígonos irregulares aún pueden ser pentágonos, hexágonos y nonágonos, pero no tienen ángulos congruentes ni lados iguales. A continuación se presentan algunos ejemplos de polígonos irregulares.

En estos polígonos, algunos lados son claramente más largos que otros y algunos ángulos son más anchos que otros, por lo que deben ser irregulares. Observe que los polígonos irregulares tienden a verse desiguales o desiguales, mientras que los polígonos regulares se ven más ordenados y simétricos.
Veamos un ejemplo de identificación de polígonos irregulares y regulares.
Identifique el polígono de abajo y diga si es regular o irregular.
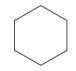
Primero, cuente el número de lados.
La forma tiene 6 lados.
A continuación, determine si los lados son congruentes.
Los lados son congruentes.
Después, etiquetar el polígono como regular o irregular.
Regulares.
La respuesta es que el polígono es un hexágono regular.
Cuando las líneas se cruzan en el plano geométrico, forman polígonos. Aplica lo que sabes para clasificar estos polígonos. Encuentra longitudes laterales o resuelve medidas de ángulo desconocidas.
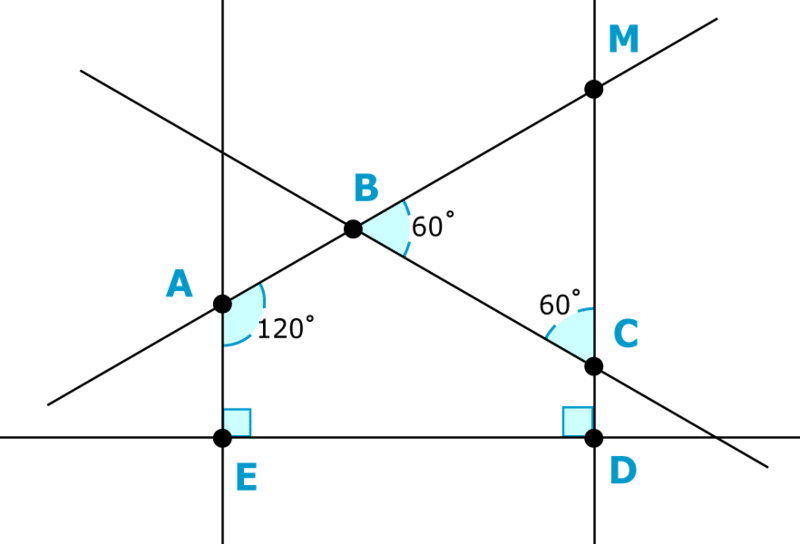
La intersección de estas cinco líneas ha creado varios polígonos diferentes. Primero, identifíquelos.
El más grande es\(AMDE\). Dentro de esta cifra hay dos figuras.
Una es la figura\(ABCDE\). \(ABCDE\)tiene cinco ángulos y cinco lados, por lo que es un pentágono. Dos de sus ángulos miden\(90^{\circ}\), y uno mide\(120^{\circ} \) Lo que significa que el polígono es un pentágono irregular. Para encontrar las medidas de los dos ángulos restantes, es necesario echar un vistazo a la tercera figura.
La tercera figura es triángulo\(MBC\). Tiene dos\(60^{\circ}\) ángulos. Los ángulos\(ABC\) y\(MBC\) son suplementarios. Es decir, juntos forman una línea recta. Una línea recta mide\(180^{\circ}\). Por lo tanto la suma de estos dos ángulos es 180^ {\ circ}\). Simplemente restar para encontrar la medida de\(ABC\).
\(180−60=120^{\circ}\)
Ángulo ABC es\(120^{\circ}\).
Ahora encontremos la medida del ángulo\(BCD\). Ya conoces cuatro de los cinco ángulos en figura\(ABCDE\). Porque esto es un pentágono, también sabes que sus ángulos interiores deben tener una suma de\(540^{\circ}\). Se puede configurar una ecuación para encontrar la medida del ángulo desconocido.
\(\begin{aligned} 90+90+120+120+\angle BCD&=540^{\circ} \\ 420+\angle BCD&=540^{\circ} \\ \angle BCD&=540−420 \\ \angle BCD&=120^{\circ} \end{aligned}\)
El quinto y último ángulo debe medir\(120^{\circ}\). Vamos a sumar todos los ángulos en el pentágono para asegurarnos de que se suman\(540^{\circ}\).
\(90+90+120+120+120=540^{\circ}\)
Todavía hay un ángulo desconocido, ángulo AMD\). Hay dos formas diferentes de encontrar la medida del tercer ángulo en triángulo\(BMD\). Sabes que los tres ángulos en un triángulo tienen una suma de\(180^{\circ}\). También es el cuarto ángulo en cuadrilátero\(AMDE\), y ya sabes que los cuatro ángulos en un cuadrilátero tienen una suma de\(360^{\circ}\). Se puede configurar una ecuación para encontrar\(AMD\).
\(\begin{aligned}60+60+\angle AMD&=180^{\circ} \\ 120+\angle AMD&=180^{\circ} \\ \angle AMD&=180−120 \\ \angle AMD&=60^{\circ}\end{aligned}\)
Ejemplo\(\PageIndex{1}\)

Antes, te dieron un problema sobre Logan y el letrero de la calle anterior.
Si traza la forma del signo, ¿la forma resultante será un polígono regular o irregular, y qué tipo de polígono será?
Solución
Primero, cuente el número de lados.
La forma tiene 6 lados.
A continuación, determine si los lados son congruentes.
Los lados no son congruentes.
Después, etiquetar el polígono como regular o irregular.
Irregular.
La respuesta es que el polígono es un hexágono irregular.
Ejemplo\(\PageIndex{2}\)
Nombra esta figura.

Solución
Primero, cuente el número de lados.
La forma tiene 5 lados.
A continuación, determine si los lados son congruentes.
Los lados no son congruentes.
Después, etiquetar el polígono como regular o irregular.
Irregular.
La respuesta es que el polígono es un pentágono irregular.
Ejemplo\(\PageIndex{3}\)
Nombra esta figura.

Solución
Primero, cuente el número de lados.
La forma tiene 7 lados.
A continuación, determine si los lados son congruentes.
Los lados no son congruentes.
Después, etiquetar el polígono como regular o irregular.
Irregular.
La respuesta es que el polígono es un heptágono irregular.
Ejemplo\(\PageIndex{4}\)
Clasificar la figura como irregular o regular e identificar el polígono.
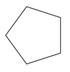
Solución
Primero, cuente el número de lados.
La forma tiene 5 lados.
A continuación, determine si los lados son congruentes.
Los lados parecen ser congruentes.
Después, etiquetar el polígono como regular o irregular.
Regulares.
La respuesta es que el polígono es un pentágono regular.
Ejemplo\(\PageIndex{5}\)
Identificar el polígono.
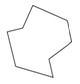
Solución
Primero, cuente el número de lados.
La forma tiene 8 lados.
A continuación, determine si los lados son congruentes.
Los lados no son congruentes.
Después, etiquetar el polígono como regular o irregular.
Irregular.
La respuesta es que el polígono es un octágono irregular.
Revisar
Identificar cada cuadrilátero por su descripción.
- Un cuadrilátero con un par de lados paralelos.
- Un cuadrilátero con lados opuestos congruentes y paralelos, con cuatro ángulos rectos.
- Un cuadrilátero con cuatro lados paralelos congruentes y cuatro ángulos rectos.
- Un rectángulo con cuatro lados paralelos congruentes.
Identificar los polígonos en el diagrama. Entonces encuentra las medidas de los ángulos desconocidos.
-
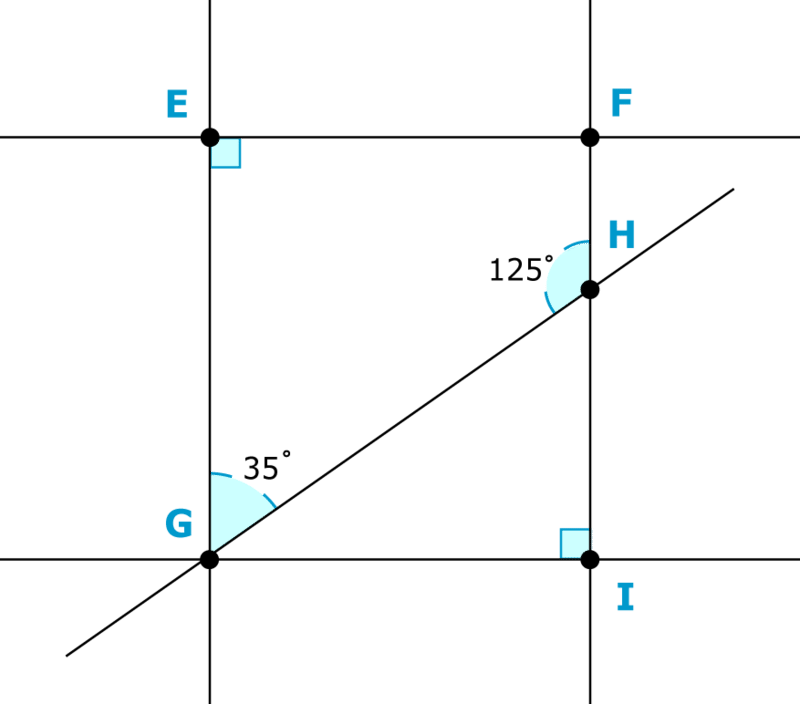
Figura\(\PageIndex{12}\)
Responder verdadero o falso para cada una de las siguientes preguntas.
- Un rombo es siempre un cuadrado.
- Un paralelogramo tiene lados opuestos que son paralelos.
- Un rectángulo es un tipo de paralelogramo.
- Cuadrados, rectángulos y rombos son paralelogramos con cuatro ángulos rectos.
- Un trapecio tiene cuatro ángulos rectos.
- Un trapecio tiene un par de lados paralelos.
- Un polígono regular tiene lados y ángulos congruentes.
- Un pentágono no puede ser un polígono irregular.
Identifique cada polígono a continuación.
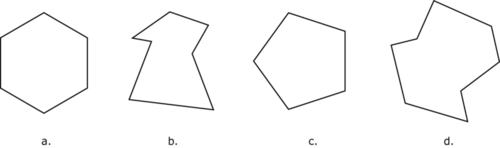
- a
- b
- c
- d
Reseña (Respuestas)
Para ver las respuestas de Revisar, abra este archivo PDF y busque la sección 8.11.
Recursos
vocabulario
| Término | Definición |
|---|---|
| Paralelogramo | Un paralelogramo es un cuadrilátero con dos pares de lados paralelos. |
| Polígono | Un polígono es una simple figura cerrada con al menos tres lados rectos. |
| Cuadrilátero | Un cuadrilátero es una figura cerrada con cuatro lados y cuatro vértices. |
| Rectángulo | Un rectángulo es un cuadrilátero con cuatro ángulos rectos. |
| Rombo | Un rombo es un cuadrilátero con cuatro lados congruentes. |
| Cuadrado | Un cuadrado es un polígono con cuatro lados congruentes y cuatro ángulos rectos. |
Recursos adicionales
Elemento Interactivo
Video: Introducción a los Polígonos
Práctica: Polígonos regulares e irregulares
Mundo real: Un Pentágono Perfecto

