5.24: Polígonos congruentes
- Page ID
- 107531
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Reconocer y comprender polígonos congruentes.
Figuras congruentes
Chelsie quiere poner un patrón de tablero de ajedrez en su casillero para su cumpleaños. Ella tiene que hacer el patrón en el tablero de carteles y luego atarlo a su casillero para que no dañe permanentemente su casillero. Ella decide que la técnica más fácil es obtener papel de construcción y cortar suficientes cuadrados para hacer su patrón. ¿Cómo puede saber si los cuadrados que recorta son congruentes?
En este concepto, aprenderás sobre figuras congruentes.
Figuras congruentes
Las figuras congruentes tienen exactamente el mismo tamaño y forma. Tienen lados congruentes y ángulos congruentes.
Aquí hay algunos pares de figuras congruentes.
Compara las cifras de cada par. Son exactamente lo mismo. Si no estás seguro, imagina que podrías cortar una figura y colocarla encima de la otra. Si coinciden exactamente, son congruentes.
Prueba de congruencia comparando cada lado y ángulo de dos figuras. Cada lado y ángulo de una figura corresponde a un lado o ángulo en el otro. Estas se denominan partes correspondientes. Por ejemplo, el punto superior de un triángulo corresponde al punto superior del otro triángulo en un par congruente.
No siempre es fácil ver las partes correspondientes de dos figuras. Una figura puede girarse de manera diferente para que las partes correspondientes parezcan estar en diferentes lugares. Si no estás seguro, traza una figura y colócala encima de la otra para ver si puedes hacer que coincidan.
¿El par de figuras de abajo es congruente?
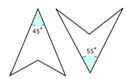
Primero, mira la forma de cada figura.
Las formas se ven similares.
A continuación, determine si hay partes correspondientes.
Los ángulos dados no son correspondientes porque tienen valores diferentes.
Después, determine si las formas son correspondientes.
No.
La respuesta es que el par de figuras no son congruentes.
Puede usar información sobre una figura en un par de figuras congruentes para encontrar la medida de un ángulo o lado correspondiente en la otra figura. Veamos cómo funciona esto. Echa un vistazo a las cifras congruentes a continuación.
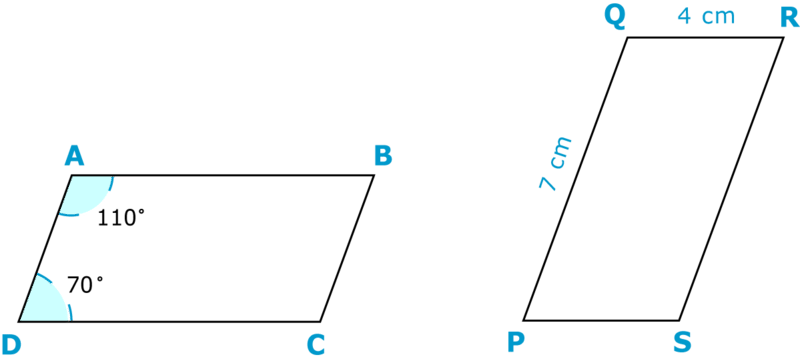
Estos dos paralelogramos son congruentes. Encuentra las partes correspondientes.
Primero, traza un paralelogramo y colóquelo encima del otro. Gírela hasta que las partes correspondan.
Se puede ver que lado\(AB\) corresponde a lado\(PQ\) porque son congruentes. Por lo tanto,
\(AB\cong PQ\).
Enumere todos los lados congruentes.
\(\begin{aligned} AB&\cong PQ \\ BC &\cong QR \\ AD&\cong PS \\ DC &\cong SR \end{aligned}\)
Enumere los ángulos congruentes.
\(\begin{aligned}\angle A &\cong \angle P \qquad& \angle D&\cong \angle S \\ \angle B &\cong \angle Q \qquad& \angle C&\cong \angle R \end{aligned}\)
Ahora vamos a encontrar la longitud del lado\(AB\).
\(AB\)es congruente con\(PQ\), así que si encuentras la longitud de\(PQ\) entonces será la misma para\(AB\). \(PQ\)es de 7 centímetros. Por lo tanto AB también debe tener 7 centímetros de largo.
Ahora veamos los ángulos. Encontremos la medida de\(\angle C\). El ángulo corresponde a\ ángulo R, pero no se conoce la medida de\(\angle R\) ninguno de los dos. No obstante, sí conoces las medidas de dos de los ángulos en el primer paralelogramo:\(70^{\circ}\) y\(110^{\circ}\). No conoces la medida de\ ángulo B, pero esta vez sí conoces la medida de su ángulo correspondiente,\(\angle Q\). Estos dos ángulos son congruentes, así que sabes que\ ángulo B debe medir\(70^{\circ}\). Ahora conoces tres de los ángulos en la primera figura, por lo que puedes restar para encontrar la medida de\(\angle C\).
\(\begin{aligned} 360−(70+110+70) &=\angle C \\ 360−250&=\angle C \\ 110^{\circ}&=\angle C \end{aligned}\)
Ejemplo\(\PageIndex{1}\)
Anteriormente, te dieron un problema sobre Chelsie y su casillero temático de tablero de ajedrez.
Ella ha cortado las formas, ¿cómo puede saber si los cuadrados que recortó son congruentes?
Solución
Primero, mida las longitudes de los lados.
Todos los lados son iguales.
A continuación, mida los ángulos.
Todos los ángulos deben ser iguales.
Entonces, sacar una conclusión.
Las formas son congruentes.
La respuesta es que las formas son congruentes.
Ejemplo\(\PageIndex{2}\)
¿El par de abajo es congruente?
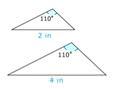
Solución
Primero, mira la forma de cada figura.
Las formas se ven similares pero una forma es más pequeña que la otra.
A continuación, determine si hay partes correspondientes.
Parece haber ángulos correspondientes, pero los lados que están en la misma posición no son congruentes.
Después, determine si las formas son correspondientes.
No.
La respuesta es que el par de figuras no son congruentes.
Ejemplo\(\PageIndex{3}\)
¿El par de figuras es congruente?
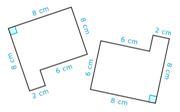
Solución
Primero, mira la forma de cada figura.
Las formas se ven similares.
A continuación, determine si hay partes correspondientes.
Parece haber ángulos correspondientes, pero no todos los lados que están en la misma posición son congruentes.
Después, determine si las formas son correspondientes.
No.
La respuesta es que el par de figuras no son congruentes.
Ejemplo\(\PageIndex{4}\)
¿Cuál es la medida de\(\angle M\)?
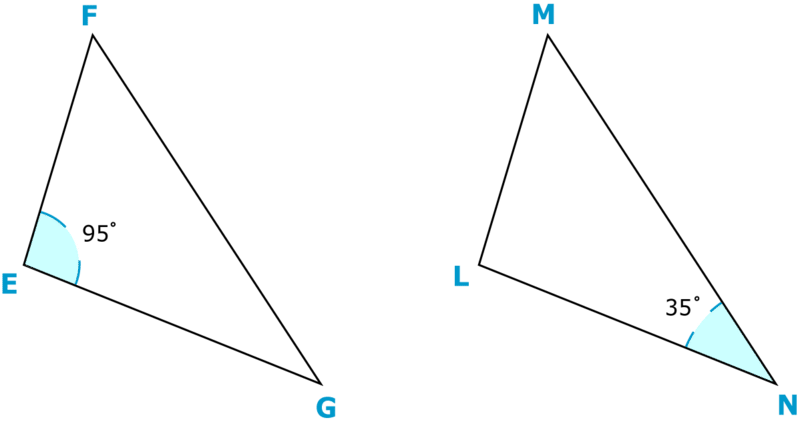Figura\(\PageIndex{7}\)Solución
Primero, identificar el ángulo que corresponde con el ángulo\(L\).
\(Angle L = Angle E = 95^{\circ}\)
A continuación, entienda que la suma de tres ángulos interiores es de 180o y escriba una ecuación.
\(95+35+x=180\)
Entonces, resuelva la medida del ángulo faltante.
\(\begin{aligned} 130+x&=180 \\ x&=50 \end{aligned}\)
La respuesta es que la medida del ángulo M es\(50^{\circ}\).
Ejemplo\(\PageIndex{5}\)
\(DEF\)El triángulo es congruente con el triángulo\(KLM\). Si\(angle D=42^{\circ}\), ¿cuál es la medida del ángulo\(K\)?
Solución
Primero, determine si el ángulo\(K\) es congruente con el ángulo\(D\).
Sí, lo es.
A continuación, recuerde la relación entre partes congruentes.
Las partes congruentes son iguales.
Después, escribe la medida del ángulo\(K\).
\(42^{\circ}\)
La respuesta es ese ángulo\(K=42^{\circ}\).
Revisar
Nombrar las partes correspondientes a las que se indican a continuación.
- \(\angle R\)
- \(MN\)
- \(\angle O\)
Utilizar las relaciones entre figuras congruentes para encontrar la medida de\(g\). Muestre su trabajo.
-
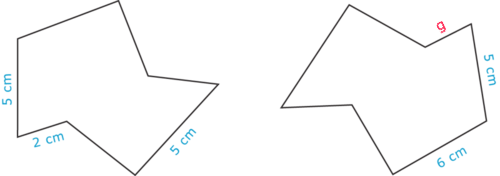
Figura\(\PageIndex{9}\)
Utilizar las relaciones entre figuras congruentes para encontrar la medida de\(\angle T\). Muestre su trabajo.
-
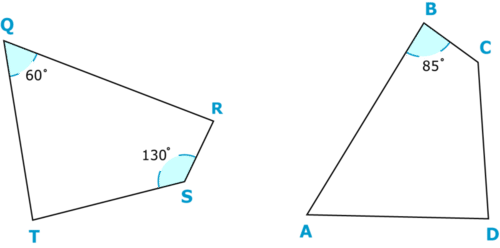
Figura\(\PageIndex{10}\)
Responde a cada una de las siguientes preguntas.
- Triángulos\(ABC\) y\(DEF\) son congruentes. Si la medida del ángulo A es\(58^{\circ}\), ¿cuál es la medida del ángulo\(D\) si corresponde al ángulo\(A\)?
- Verdadero o falso. Las cifras congruentes son exactamente las mismas en todos los sentidos.
Identificar los triángulos dados como visualmente congruentes o no.
-
Figura\(\PageIndex{11}\) -
Figura\(\PageIndex{12}\) -
Figura\(\PageIndex{13}\) -
Figura\(\PageIndex{14}\) -
Figura\(\PageIndex{15}\)
Responde a cada una de las siguientes preguntas.
- Triángulos\(ABC\) y\(DEF\) son congruentes. ¿Significa esto que sus medidas de ángulo son las mismas? ¿Por qué?
- Definir Congruente.
- Verdadero o falso. Si dos figuras son congruentes, entonces tienen los lados de la misma longitud pero no las mismas medidas de ángulo.
- Triángulos\(ABC\) y\(DEF\) son congruentes. Si la medida del ángulo A es\(58^{\circ}\), ¿cuál es la medida del ángulo D si corresponde al ángulo A?
Reseña (Respuestas)
Para ver las respuestas de Revisar, abra este archivo PDF y busque la sección 8.12.
Recursos
El vocabulario
| Término | Definición |
|---|---|
| Ángulo | Una figura geométrica formada por dos rayos que conectan en un solo punto o vértice. |
| Congruente | Las figuras congruentes son idénticas en tamaño, forma y medida. |
| Trapezoide | Un trapecio es un cuadrilátero con exactamente un par de lados opuestos paralelos. |
| Transformación Rígida | Una transformación rígida es una transformación que conserva la distancia y los ángulos, no cambia el tamaño ni la forma de la figura. |
Recursos adicionales
Elemento Interactivo
Video: Triángulos Congruentes y Similares
Práctica: Polígonos congruentes
Mundo real: Copycats