5.25: Partes correspondientes de figuras congruentes
- Page ID
- 107492
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Identificar longitudes laterales coincidentes y medidas de ángulo en figuras congruentes.

Melvin vive en una casa que tiene muchos espejos. Le gusta mirarse en los espejos y jugar con los espejos. Un día, su madre le dice que el espejo en forma de paralelogramo junto a la puerta principal es congruente con el espejo en forma de paralelogramo junto a las imágenes en el pasillo. Melvin dibuja las formas lo mejor que puede y etiqueta las partes que conoce para cada forma.
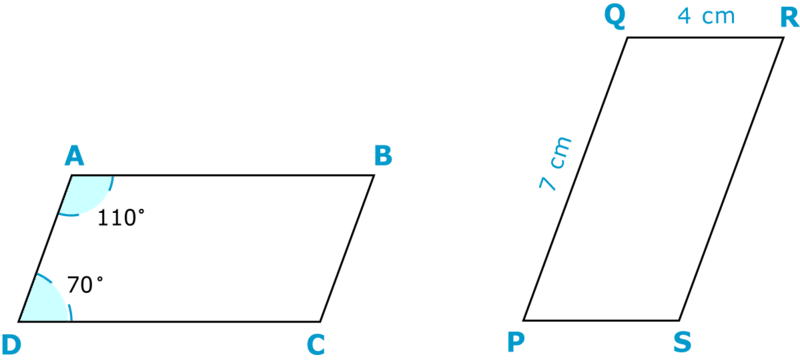
¿Cuál es la longitud de\(\overline{AB}\)?
En este concepto, conocerás partes correspondientes de figuras congruentes.
Partes correspondientes de figuras congruentes
La palabra correspondiente se refiere a partes que coinciden entre dos triángulos congruentes. Se pueden identificar los ángulos correspondientes y los lados correspondientes.

Primero, nombra los ángulos correspondientes. Los ángulos correspondientes son ángulos coincidentes entre los dos triángulos. Los ángulos correspondientes tendrán la misma medida en triángulos congruentes.
\(\angle A\cong \angle D\angle B\cong \angle E\angle C\cong \angle F\)
Aquí los ángulos están conectados con el símbolo para congruente. Cuando ves el signo igual con una línea squiggly en la parte superior, sabes que los ítems en cada lado de la ecuación son congruentes.
A continuación, nombra los lados correspondientes. Los lados correspondientes son lados coincidentes entre dos triángulos. Tendrán la misma longitud en triángulos congruentes.
\(\begin{aligned}\overline{AB}&\cong \overline{DE} \\ \overline{AC} &\cong \overline{DF} \\ \overline{BC} &\cong \overline{EF}\end{aligned}\)
Ejemplo\(\PageIndex{1}\)
Antes, te dieron un problema sobre Melvin y su casa de espejos.
Se entera de que dos de los espejos son congruentes, por lo que dibuja las formas lo mejor que puede y rellena lo que sabe de cada forma.

¿Cuál es la longitud de\(\overline{AB}\)?
Solución
Primero, gira la segunda forma para que se vea igual que la primera forma.
A continuación, identificar el lado en el segundo triángulo que corresponde a\(\overline{AB}\).
\(\overline{PQ}\)
Después, escribe la longitud del lado correspondiente.
7 cm
La respuesta es de 7 cm. La longitud de\(\overline{AB}\) es de 7 cm.
Ejemplo\(\PageIndex{2}\)
Estas dos cifras son congruentes. ¿Qué ángulo es congruente con el ángulo\(A\)?

Solución
Primero, gira la segunda figura para que quede dispuesta como la primera forma.
Después, identificar el ángulo en la segunda figura que está en la misma posición que el ángulo\(A\) en el primer triángulo.
\(P\)
La respuesta es ángulo\(P\). \(\angle A\cong \angle P\)
Utilice el siguiente diagrama de dos triángulos congruentes para responder a las siguientes preguntas.

Ejemplo\(\PageIndex{3}\)
\(E\)El ángulo es congruente con el ángulo _____
Solución
Primero, asegúrate de que los triángulos estén dispuestos de manera que tengan el mismo aspecto.
Sí
Después, identifica el ángulo en el segundo triángulo que está en la posición en la que el ángulo\(E\) está en el primer triángulo.
\( H\)
La respuesta es ángulo\(H\). \(E\)El ángulo es congruente con el ángulo\(H\).
Ejemplo\(\PageIndex{4}\)
\(\overline{FG}\cong ______\)
Solución
Primero, asegúrate de que los triángulos estén dispuestos de manera que tengan el mismo aspecto.
Sí
Después, identifica el segmento de línea en el segundo triángulo que está en la posición que\(\overline{FG}\) está en el primer triángulo.
\(\overline{IJ}\)
La respuesta es\(\overline{IJ}\). \(\overline{FG}\cong \overline{IJ}\).
Ejemplo\(\PageIndex{5}\)
\(J\)El ángulo es congruente con el ángulo _____
Solución
Primero, asegúrate de que los triángulos estén dispuestos de manera que tengan el mismo aspecto.
Sí
Después, identifica el ángulo en el segundo triángulo que está en la posición en la que el ángulo J está en el primer triángulo.
\(G\)
La respuesta es ángulo\(G\). \(J\)El ángulo es congruente con el ángulo\(G\).
Revisar
Utilice los siguientes triángulos para responder a las preguntas.

- ¿Estos dos triángulos son similares o congruentes?
- ¿Cómo lo sabes?
- Lado\(DE\) es congruente a qué otro lado?
- Lado\(DF\) es congruente a qué otro lado?
- Lado\(EF\) es congruente a qué otro lado?
- Si la longitud lateral de DE es 10, ¿cuál es la longitud lateral de\(GH\)?
- Si la longitud lateral de HI es 8, ¿qué otro lado también es 8?
Utilice las siguientes cifras para responder a las preguntas.

- Estas dos cifras son congruentes. Explica dos formas en las que puedes determinar si las cifras son congruentes o no.
- \(Q\)El ángulo es congruente a qué otro ángulo?
- \(R\)El ángulo es congruente a qué otro ángulo?
- \(S\)El ángulo es congruente a qué otro ángulo?
- Si\(PQ\) es de 7 cm, ¿qué otros lados son de 7 cm?
- Si\(QR\) es de 4 cm, ¿qué otros lados son de 4 cm?
- Si Ángulo\(D\) es de 70 grados, nombre otro ángulo de 70 grados.
- Si Ángulo\(A\) es de 110 grados, nombre otro ángulo de 110 grados.
Recursos
El vocabulario
| Término | Definición |
|---|---|
| Congruente | Las figuras congruentes son idénticas en tamaño, forma y medida. |
| Correspondiente | Los lados correspondientes entre dos triángulos son lados en la misma posición relativa. |
| Similar | Dos figuras son similares si tienen la misma forma, pero no necesariamente del mismo tamaño. |
Recursos adicionales
Video: Triángulos Congruentes y Similares
Práctica: Partes correspondientes de figuras congruentes

