5.23: Construir Polígonos Regulares
- Page ID
- 107479
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\(\newcommand{\longvect}{\overrightarrow}\)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Construir dibujos de triángulos equiláteros, cuadrados y polígonos regulares usando una brújula y una recta. Crea polígonos usando Geogebra.
Construcciones de Polígonos Regulares
Usa tu brújula para construir un círculo como el que se muestra a continuación en una hoja de papel. Describe cómo doblar el papel dos veces para ayudarte a construir un cuadrado.

Polígonos Regulares
Un polígono regular es un polígono que es equiangular y equilátero. Esto quiere decir que todos sus ángulos son de la misma medida y todos sus lados tienen la misma longitud.
El ejemplo más básico de un polígono regular es un triángulo equilátero, un triángulo con tres lados congruentes y tres ángulos congruentes. Los cuadrados también son polígonos regulares, porque todos sus ángulos son iguales (\(90^{\circ}\)) y todos sus lados tienen la misma longitud. Los polígonos regulares con cinco o más lados no tienen nombres especiales. En cambio, se usa la palabra regular para describirlos. Por ejemplo, un hexágono regular es un hexágono (polígono de 6 lados) cuyos ángulos son todos de la misma medida y los lados son todos de la misma longitud.
Todos los polígonos regulares tienen simetría de rotación. Esto significa que una rotación menor que\(360^{\circ}\) llevará el polígono regular sobre sí mismo. De hecho, un polígono regular de n lados tiene simetría de rotación para cualquier múltiplo de\(\dfrac{360^{\circ}}{n}\).
Las construcciones son procesos paso a paso que se utilizan para crear figuras geométricas precisas. Para crear una construcción a mano, hay algunas herramientas que puedes usar:
- Brújula: Un dispositivo que permite crear un círculo con un radio dado. No sólo las brújulas pueden ayudarte a crear círculos, sino que también te pueden ayudar a copiar distancias.
- Enderezado: Cualquier cosa que le permita producir una línea recta. Una recta no debe ser capaz de medir distancias. Una tarjeta de índice funciona bien como una recta. También puedes usar una regla como regla recta, siempre y cuando solo la uses para dibujar líneas rectas y no para medir.
- Papel: Cuando una figura geométrica está sobre una hoja de papel, el papel mismo se puede plegar para construir nuevas líneas.
Puedes construir algunos polígonos regulares a mano si recuerdas las definiciones y propiedades de estos polígonos regulares. Con la ayuda adicional de software de geometría o un transportador, puede construir cualquier polígono regular.
Echemos un vistazo a un problema de ejemplo.
\(\overline{AB}\)es un lado de lo que se convertirá en triángulo equilátero\(\Delta ABC\). Es necesario poner punto\(C\) en el lugar correcto para poder hacer el triángulo equilátero. ¿Dónde\(C\) se debe colocar el punto con respecto a los puntos\(A\) y\(B\)?
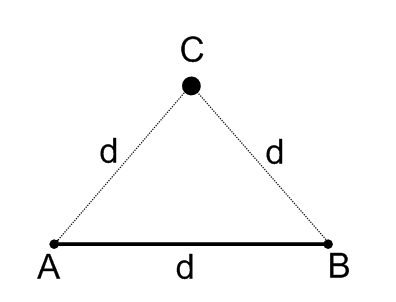
Deja que la distancia entre\(A\) y\(B\) sea\(d\). El punto\(C\) necesita estar d lejos del punto\(A\) y también\(d\) lejos del punto\(B\).
Use una recta para dibujar un segmento de línea\(\overline{AB}\). Usa las ideas del Ejemplo A para construir un triángulo equilátero\(\Delta ABC\).
Use una brújula para medir la longitud de\(\overline{AB}\).
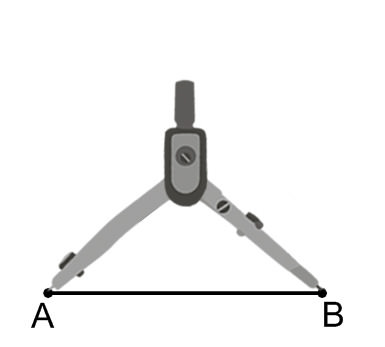
Hacer un círculo parcial de puntos que son la longitud de\(\overline{AB}\) distancia del punto\(A\).
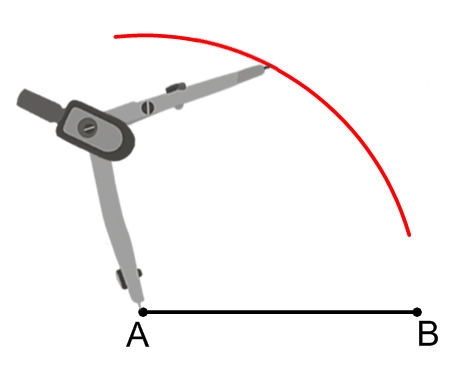
Hacer otro círculo parcial de puntos que son la longitud de\(\overline{AB}\) lejos del punto\(B\).
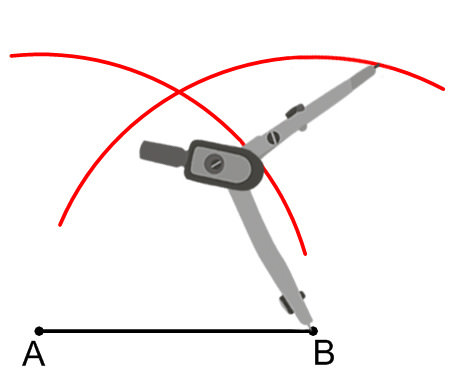
El punto de intersección de estos dos círculos parciales es el punto\(C\).
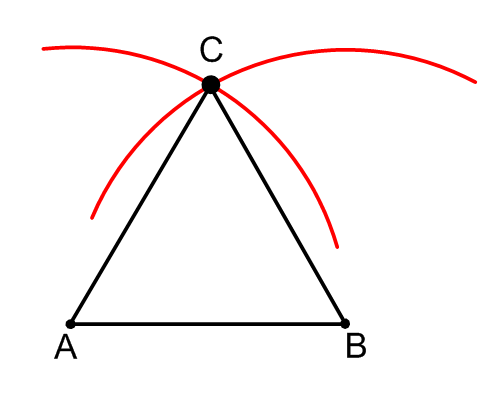
Los puntos\(A\)\(B\),,\(C\), y\(D\) están en un círculo centrado en el punto\(O\). Demostrar que\(ABCD\) es un cuadrado.
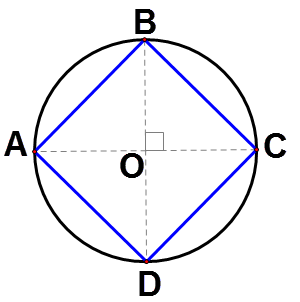
\(\overline{AO}\cong \overline{BO}\cong \overline{CO}\cong \overline{DO}\)porque todos son radios del mismo círculo. Ya que\(\angle BOC\) es un ángulo recto\(\angle BOA\),,\ ángulo AOD\) y también\(\angle COD\) debe ser ángulos rectos. Por lo tanto,\(\angle BOC\cong \angle BOA\cong \angle AOD\cong \angle COD\). Esto quiere decir que\(\Delta BOC\cong \Delta AOB\cong \Delta DOA\cong \Delta COD\) por SAS\ cong\). \(\overline{AB}\cong \overline{BC}\cong \overline{CD}\cong \overline{DA}\)porque son partes correspondientes de triángulos congruentes.
Los cuatro triángulos son isósceles porque cada uno tiene dos lados congruentes. Esto quiere decir que sus ángulos de base son congruentes. Debido a que el ángulo de vértice de cada triángulo es\(90^{\circ}\), los ángulos base de cada triángulo deben ser\(45^{\circ} (90+45+45=180)\). Los cuatro ángulos que componen el cuadrilátero están formados cada uno por dos de estos\(45^{\circ}\) ángulos, y son cada uno por lo tanto\(90^{\circ}\).
Debido a que el cuadrilátero tiene cuatro lados congruentes y cuatro\(90^{\circ}\) ángulos, es un cuadrado.
Ejemplo\(\PageIndex{1}\)
Anteriormente, se le pidió que describiera cómo doblar el papel dos veces para ayudarle a construir un cuadrado.
Solución
Dobla el círculo para que las dos mitades se superpongan para crear un pliegue que sea el diámetro.
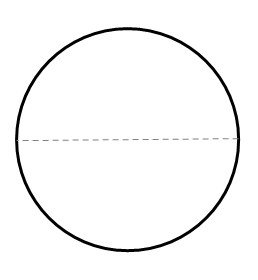
Dobla el círculo por la mitad nuevamente para crear la bisectriz perpendicular del diámetro. Para ello, dobla para que los dos extremos del diámetro se encuentren. El segundo pliegue también será de diámetro.
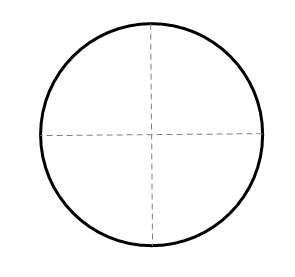
Tenga en cuenta que los dos diámetros son perpendiculares entre sí. Conecte los cuatro puntos de intersección en el círculo para construir el cuadrado.
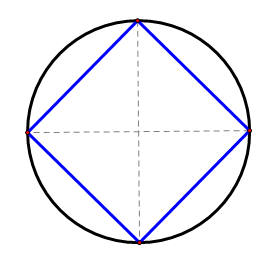
Puede estar seguro de que se trata de un cuadrado debido a la prueba en el Ejemplo C.
Ejemplo\(\PageIndex{2}\)
El hexágono regular de abajo se ha dividido en seis triángulos congruentes. ¿Qué tipo de triángulos son? Explique.
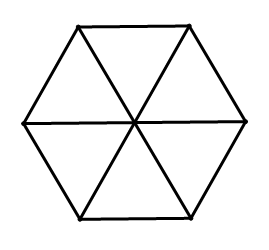
Solución
Deben ser triángulos equiláteros.
- Un círculo completo es\(360^{\circ}\), por lo que cada ángulo en el centro del hexágono debe ser\(\dfrac{360^{\circ} }{6}=60^{\circ}\). * También es por eso que los hexágonos regulares demuestran simetría de rotación en múltiplos de\(60^{\circ}\) . *
- Los seis triángulos son congruentes, por lo que los seis segmentos que conectan el centro del hexágono a los vértices deben ser congruentes. Esto significa que los seis triángulos son todos isósceles.
- Los ángulos base de cada uno de los triángulos isósceles deben ser\(\dfrac{180−60}{2}=60^{\circ}\).
- La medida de cada ángulo de todos los triángulos es\(60^{\circ}\), por lo que todos los triángulos son equiláteros.
Ejemplo\(\PageIndex{3}\)
Seis puntos se han espaciado uniformemente alrededor del círculo de abajo. Explica por qué se crea un hexágono regular cuando estos puntos están conectados.
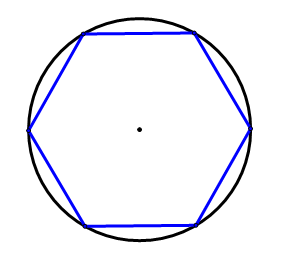
Solución
Debido a que los seis puntos están espaciados uniformemente, cada uno de los segmentos que conectan los seis puntos debe tener la misma longitud. Por lo tanto, el polígono debe ser regular. Debido a que hay seis lados, debe ser un hexágono regular.
Ejemplo\(\PageIndex{4}\)
Construir un hexágono regular inscrito en un círculo.
Solución
“Inscrito en un círculo” significa que los seis vértices del hexágono están en el mismo círculo. Comienza construyendo un círculo y un punto en el círculo.

Sabes que el radio del círculo es el mismo que la longitud de cada lado del círculo (ver práctica guiada #1). Por lo tanto, tu objetivo es colocar seis puntos alrededor del círculo que estén a la misma distancia entre sí que el radio del círculo. Mantén tu brújula abierta al mismo ancho que el radio del círculo y haz una nueva marca en el círculo.
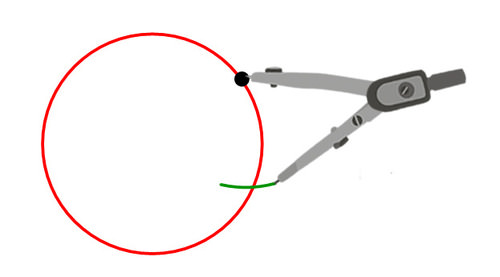
Continuar haciendo nuevas marcas alrededor del círculo que estén a la misma distancia entre sí.

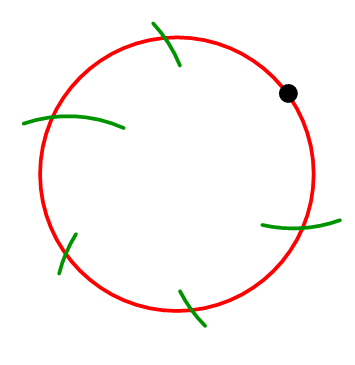
Conecte los puntos de intersección para formar el hexágono regular.
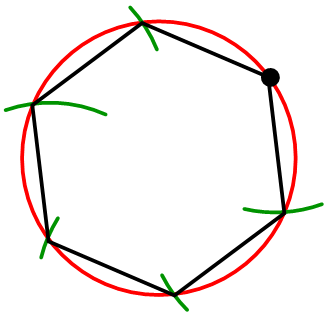
Revisar
1. Construir un triángulo equilátero.
2. Construir otro triángulo equilátero.
3. Explica por qué funciona tu proceso de construcción de triángulos equiláteros.
4. Construye un cuadrado inscrito en un círculo haciendo dos pliegues.
5. Justifica por qué el polígono que has creado es en realidad un cuadrado.
Usa tu enderezamiento para construir\(\overline{AB}\).
6. Construir la bisectriz perpendicular de\(\overline{AB}\).
7. Construye un círculo con diámetro\(\overline{AB}\).
8. Construir un cuadrado inscrito en el círculo conectando los cuatro extremos de los diámetros.
9. Extiende tu construcción a un octágono regular biseccionando cada uno de los ángulos rectos en el centro del círculo.
10. Construir un hexágono regular inscrito en un círculo.
11. Explique por qué el método para construir un hexágono regular se basa en un círculo.
12. Explica cómo podrías extender tu construcción del hexágono regular a una construcción de 12 gones regulares.
13. Construir un triángulo equilátero. Explica cómo podrías construir el círculo que pasa por los tres puntos del triángulo equilátero.
14. Dado un triángulo equilátero inscrito en un círculo, ¿cómo se podría extender la construcción para construir un hexágono regular?
15. Dado un círculo y un transportador, explica cómo podrías crear un pentágono regular.
Reseña (Respuestas)
Para ver las respuestas de Revisar, abra este archivo PDF y busque la sección 5.4.
El vocabulario
| Término | Definición |
|---|---|
| Polígono Regular | Un polígono regular es un polígono con todos los lados de la misma longitud y todos los ángulos la misma medida. |
| Equilátero | Un polígono es equilátero si todos sus lados tienen la misma longitud. |
| Equiangular | Un polígono es equiangular si todos los ángulos son de la misma medida. |

