5.26: Determinar las medidas de ángulo faltantes
- Page ID
- 107487
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\(\newcommand{\longvect}{\overrightarrow}\)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Encuentra las medidas de ángulo faltantes de cuadriláteros dada una suma de 360 grados.
Comprensión de las medidas de ángulo de los cuadriláteros

Stephanie, una estudiante de Matemáticas 12, está ayudando a recaudar dinero para participar en la Olimpiada de Matemáticas de este año en Dallas, Texas. Dado que Stephanie es muy artística en la fabricación de joyas, ha decidido hacer y vender collares para recaudar dinero. Varios clientes le han preguntado qué forma ha usado para el cordón azul de un collar de aspecto particularmente geométrico. Ella sabe qué forma es pero no está segura de cómo explicar esta forma a sus clientes.
¿Qué puede decir Stephanie a sus clientes sobre esta forma?
En este concepto, aprenderás a entender las medidas angulares de los cuadriláteros.
Cuadriláteros
Un cuadrilátero es una forma cerrada bidimensional que tiene cuatro lados rectos.
Tres cuadriláteros especiales son un paralelogramo que es un cuadrilátero con lados opuestos paralelos y congruentes, un trapecio que es un cuadrilátero que tiene un par de lados opuestos paralelos y una cometa que es un cuadrilátero que tiene dos pares de lados adyacentes congruentes.
Tres paralelogramos especiales son un rectángulo que tiene cada ángulo un ángulo recto y lados opuestos ambos congruentes y paralelos, un cuadrado que tiene cada ángulo un ángulo recto, lados opuestos paralelos y todos los lados congruentes y un rombo que tiene cada lado igual en longitud, lados opuestos paralelos, pero no todos los ángulos son un ángulo recto.
Recuerde que un cuadrilátero es una forma cerrada bidimensional que tiene cuatro lados rectos y cuatro ángulos.
La suma de los ángulos interiores de un cuadrilátero es\(360^{\circ}\) independientemente del tipo de cuadrilátero. El siguiente diagrama mostrará varios cuadriláteros y sus ángulos interiores.
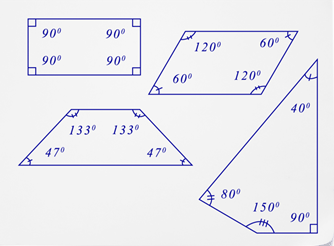
Si agrega la medida de los cuatro ángulos interiores de cada cuadrilátero que se muestran arriba, la suma será igual\(360^{\circ}\). Cada uno de estos cuadriláteros se puede dividir en dos triángulos. Recuerda la suma de los ángulos interiores de un triángulo es igual\(180^{\circ}\). Si la figura cerrada contiene dos triángulos entonces la suma de los ángulos interiores es igual\(2(180^{\circ})=360^{\circ}\).
Apliquemos estos hechos a un ejemplo.
Para el siguiente cuadrilátero, determinar la medida de\ ángulo M\).
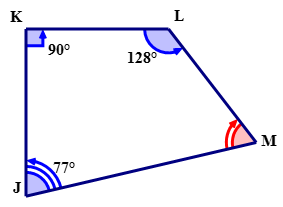
Primero, escribe una ecuación para representar la suma de los ángulos interiores del cuadrilátero\(JKLM\).
\(\angle J+\angle K+\angle L+\angle M=360^{\circ}\)
A continuación, sustituya en la ecuación, las medidas dadas de los ángulos J\), K\) y L\).
\(\begin{aligned} \angle J+\angle K+\angle L+\angle M &=360^{\circ} \\ 77^{\circ}+90^{\circ}+128^{\circ}+\angle M &=360^{\circ} \end{aligned}\)
A continuación, simplifique el lado izquierdo de la ecuación.
\(\begin{aligned}77^{\circ}+90^{\circ}+128^{\circ}+\angle M&=360^{\circ} \\ 295^{\circ}+\angle M&=360^{\circ}\end{aligned}\)
Entonces, restar\(295^{\circ}\) de ambos lados de la ecuación para resolver para la medida de\(\angle M\).
\(\begin{aligned} 295^{\circ}+\angle M &=360^{\circ} \\ 295^{\circ}−295^{\circ}+\angle M &=360^{\circ}−295^{\circ} \\ \angle M &=65^{\circ} \end{aligned}\)
La respuesta es 65.
La medida de\(\angle M\) es\(65^{\circ}\).
Este método se puede utilizar para calcular la medida del ángulo faltante de cualquier cuadrilátero cuando se conocen las medidas de tres de los ángulos.
Ejemplo\(\PageIndex{1}\)
Antes, te dieron un problema sobre Stephanie y sus collares. Ella necesita averiguar qué decirles a sus clientes sobre la forma de la cuenta azul. ¿Qué les puede decir?
Solución
Primero, dibuja la forma e incluye todas las marcas importantes.
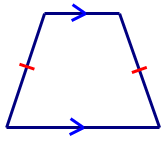
A continuación, explique las marcas en los lados de la forma.
Las flechas en los lados superior e inferior de la figura indican que este par de lados opuestos son paralelos. La marca tic en los otros dos lados indica que estos lados son congruentes (igual en longitud).
Entonces, nombra la forma.
La forma de la cuenta azul es un trapecio isósceles.
Ejemplo\(\PageIndex{2}\)
Un cuadrilátero\(ABCD\) que tiene un par de lados opuestos paralelos tiene medidas de ángulo tales que\(\angle A=44^{\circ}\). Encuentra la medida de\(\angle C\) en el siguiente cuadrilátero.
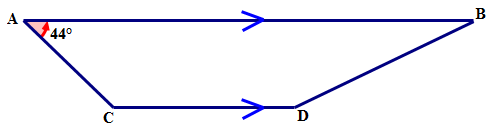
Solución
Primero, nombra el tipo de cuadrilátero y anote lo que sepas.
Un cuadrilátero con un par de lados opuestos paralelos se llama trapecio. \(\angle A\)y\(\angle C\) están en el mismo lado de la pierna\(\angle AC\) y son complementarios.
A continuación, escribe una ecuación para modelar lo que sabes de los dos ángulos.
\(\angle A+\angle C=180^{\circ}\)
A continuación, rellena en la ecuación la medida de\(\angle A\).
\(\begin{aligned} \angle A+\angle C&=180^{\circ} \\ 44^{\circ}+\angle C&=180^{\circ}\end{aligned}\)
Luego, restar\(44^{\circ}\) de ambos lados de la ecuación para resolver para\ ángulo C\).
\(\begin{aligned} 44^{\circ}+\angle C&=180^{\circ} \\ 44^{\circ}−44^{\circ}+\angle C&=180^{\circ}−44^{\circ} \\ \angle C &=136^{\circ} \end{aligned}\)
La respuesta es 136.
La medida de\(\angle C\) es\(136^{\circ}\).
Ejemplo\(\PageIndex{3}\)
Para el siguiente cuadrilátero, encuentra la medida del ángulo desconocido.
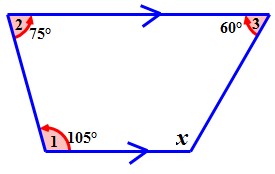
Solución
Primero, escribe una ecuación para modelar la suma de los ángulos interiores de un cuadrilátero.
\(\angle 1+\angle 2+\angle 3+\angle 4=360^{\circ}\)
A continuación, rellena en la ecuación las medidas de cualquier ángulo conocido.
\(\begin{aligned} \angle 1+\angle 2+\angle 3+\angle 4 &=360^{\circ} \\ 105^{\circ}+75^{\circ}+60^{\circ}+\angle 4&=360^{\circ} \end{aligned}\)
A continuación, vamos\(\angle 4=x\)
\(\begin{aligned} 105^{\circ}+75^{\circ}+60^{\circ}+\angle 4=360^{\circ} \\ 105^{\circ}+75^{\circ}+60^{\circ}+x=360^{\circ} \end{aligned}\)
A continuación, simplifique el lado izquierdo de la ecuación.
\(\begin{aligned}105^{\circ}+75^{\circ}+60^{\circ}+x&=360^{\circ} \\ 240^{\circ}+x&=360^{\circ} \end{aligned}\)
A continuación, restar\(240^{\circ}\) de ambos lados de la ecuación para resolver por '\(x\)'.
\(\begin{aligned} 240^{\circ}+x&=360^{\circ} \\ 240^{\circ}−240^{\circ}+x&=360^{\circ} \\ x&=360^{\circ}−240^{\circ}=120^{\circ} \end{aligned}\)
La respuesta es 120.
La medida de\(\angle 4\) es\(120^{\circ}\).
Ejemplo\(\PageIndex{4}\)
¿Cuál es la medida del cuarto ángulo de un cuadrilátero que tiene tres ángulos que miden\(110^{\circ}\),\(80^{\circ}\) y\(95^{\circ}\)?
Solución
Primero, escribe una ecuación para modelar la suma de los ángulos interiores del cuadrilátero.
\(\angle 1+\angle 2+\angle 3+\angle 4=360^{\circ}\)
A continuación, rellena en la ecuación las medidas de los tres ángulos conocidos.
\(\begin{aligned} \angle 1+\angle 2+\angle 3+\angle 4&=360^{\circ} \\ 110^{\circ}+95^{\circ}+80^{\circ}+\angle 4&=360^{\circ}\end{aligned}\)
A continuación, simplifique el lado izquierdo de la ecuación.
\(\begin{aligned} 110^{\circ}+95^{\circ}+80^{\circ}+\angle 4&=360^{\circ} \\ 285^{\circ}+\angle 4&=360^{\circ} \end{aligned}\)
Entonces, restar\(285^{\circ}\) de ambos lados de la ecuación para resolver para la medida de\(\angle 4\).
\(\begin{aligned} 285^{\circ}+\angle 4 &=360^{\circ} \\ 285^{\circ}−285^{\circ}+\angle 4&=360^{\circ}−285^{\circ} \\ \angle 4&=75^{\circ} \end{aligned}\)
Ejemplo\(\PageIndex{5}\)
¿Cuál es el nombre del cuadrilátero que tiene todos los lados iguales en longitud, lados opuestos paralelos y cada ángulo un ángulo recto?
Solución
Primero, dibujar el cuadrilátero para representar la información dada en el problema.
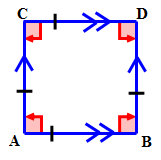
Entonces, nombra el cuadrilátero.
Este es un paralelogramo especial llamado cuadrado.
Revisar
Usa lo que has aprendido sobre los cuadriláteros para averiguar la medida de ángulo faltante de cada cuadrilátero en función de tres ángulos dados.
- \(120^{\circ}, 120^{\circ}, 60^{\circ}, ?\)
- \(50^{\circ}, 70^{\circ}, 130^{\circ}, ?\)
- \(52^{\circ}, 128^{\circ},52^{\circ}, ?\)
- \(47^{\circ}, 55^{\circ}, 120^{\circ}, ?\)
- \(80^{\circ}, 80^{\circ}, 100^{\circ}, ?\)
- \(105^{\circ}, 105^{\circ}, 85^{\circ}, ?\)
- \(97^{\circ}, 97^{\circ}, 35^{\circ}, ?\)
- \(120^{\circ}, 120^{\circ}, 40^{\circ}, ?\)
- \(88^{\circ}, 90^{\circ}, 60^{\circ}, ?\)
- \(25^{\circ}, 85^{\circ}, 85^{\circ}, ?\)
- \(90^{\circ}, 90^{\circ}, 90^{\circ}, ?\)
- \(140^{\circ}, 150^{\circ}, 45^{\circ}, ?\)
- \(80^{\circ}, 80^{\circ}, 120^{\circ}, ?\)
- \(75^{\circ}, 95^{\circ}, 110^{\circ}, ?\)
- \(80^{\circ}, 50^{\circ}, 95^{\circ}, ?\)
Reseña (Respuestas)
Para ver las respuestas de Revisar, abra este archivo PDF y busque la sección 6.8.
El vocabulario
| Término | Definición |
|---|---|
| Congruente | Las figuras congruentes son idénticas en tamaño, forma y medida. |
| Paralelogramo | Un paralelogramo es un cuadrilátero con dos pares de lados paralelos. |
| Cuadrilátero | Un cuadrilátero es una figura cerrada con cuatro lados y cuatro vértices. |
| Rectángulo | Un rectángulo es un cuadrilátero con cuatro ángulos rectos. |
| Rombo | Un rombo es un cuadrilátero con cuatro lados congruentes. |
| Cuadrado | Un cuadrado es un polígono con cuatro lados congruentes y cuatro ángulos rectos. |
| Trapezoide | Un trapecio es un cuadrilátero con exactamente un par de lados opuestos paralelos. |
Recursos adicionales
Elemento Interactivo
Video: Propiedades cuadriláteros
Práctica: Determinar las medidas de ángulo faltantes

