5.27: Ángulos interiores en polígonos convexos
- Page ID
- 107491
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Usa la fórmula\((x - 2)180\) para encontrar la suma de los ángulos interiores de cualquier polígono.
El ángulo interior de un polígono es uno de los ángulos en el interior, como se muestra en la imagen de abajo. Un polígono tiene el mismo número de ángulos interiores que los lados.
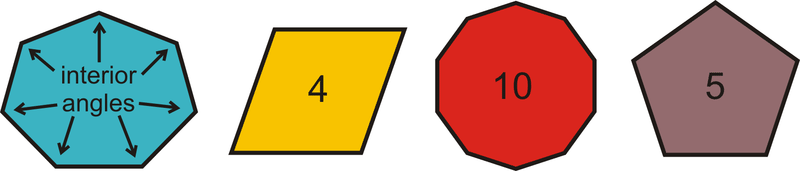
La suma de los ángulos interiores en un polígono depende del número de lados que tenga. La fórmula de suma de polígonos establece que para cualquier n-gon, los ángulos interiores se suman a\((n−2)\times 180^{\circ}\).
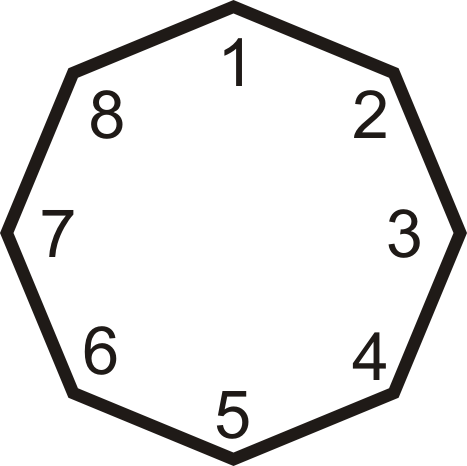
\(\begin{aligned}\rightarrow n=8 \\ (8−2) &\times 180^{\circ} \\ 6 &\times 180^{\circ} \\ &1080^{\circ}\end{aligned}\)
Una vez que conoces la suma de los ángulos interiores en un polígono es fácil encontrar la medida de UN ángulo interior si el polígono es regular: todos los lados son congruentes y todos los ángulos son congruentes. Simplemente divida la suma de los ángulos por el número de lados.
Fórmula de ángulo interior de polígono regular: Para cualquier n−gon equiangular, la medida de cada ángulo es\(\dfrac{(n−2)\times 180^{\circ}}{n}\).
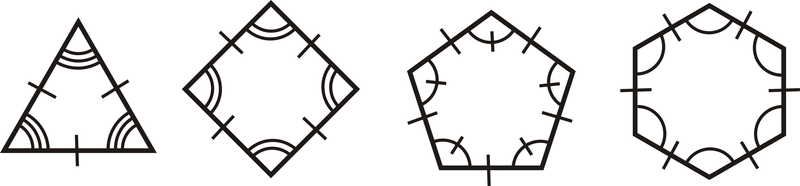
En la imagen de abajo, si los ocho ángulos son congruentes entonces cada ángulo es\(\dfrac{(8−2)\times 180^{\circ}}{8}=\dfrac{6\times 180^{\circ}}{8}=\dfrac{1080^{\circ}}{8}=135^{\circ}\).
¿Y si te dieran un polígono convexo equiangular de siete lados? ¿Cómo se podría determinar la medida de sus ángulos interiores?
Ejemplo\(\PageIndex{1}\)
Los ángulos interiores de un pentágono son\(x^{\circ}\),\(x^{\circ}\),\(2x^{\circ}\),\(2x^{\circ}\), y\(2x^{\circ}\). ¿Qué es\(x\)?
Solución
Desde la Fórmula de Suma Polígono sabemos que un pentágono tiene ángulos interiores que suman a\((5−2)\times 180^{\circ}=540^{\circ}\).
Escribe una ecuación y resuelve para x.
\(\begin{aligned} x^{\circ}+x^{\circ}+2x^{\circ}+2x^{\circ}+2x^{\circ}&=540^{\circ} \\ 8x&=540 \\ x&=67.5\end{aligned}\)
Ejemplo\(\PageIndex{2}\)
¿Cuál es la suma de los ángulos interiores en un 100 gon?
Solución
Usa la Fórmula de Suma de Polígonos. \((100−2)\times 180^{\circ}=17,640^{\circ}\).
Ejemplo\(\PageIndex{3}\)
Los ángulos interiores de un polígono se suman a\(1980^{\circ}\). ¿Cuántos lados tiene?
Solución
Usa la Fórmula de Suma de Polígonos y resuelve para n\).
\(\begin{aligned} (n−2)\times 180^{\circ}&=1980^{\circ} \\ 180^{\circ}n−360^{\circ}&=1980^{\circ} \\ 180^{\circ}n&=2340^{\circ} \\ n&=13\end{aligned}\)
El polígono tiene 13 lados.
Ejemplo\(\PageIndex{4}\)
¿Cuántos grados tiene cada ángulo en un nonágono equiangular?
Solución
Primero necesitamos encontrar la suma de los ángulos interiores; conjunto\(n=9\).
\((9−2)\times 180^{\circ}=7\times 180^{\circ}=1260^{\circ}\)
“Equiangular” nos dice que cada ángulo es igual. Entonces, cada ángulo es\(\dfrac{1260^{\circ}}{9}=140^{\circ}\).
Ejemplo\(\PageIndex{5}\)
Un ángulo interior en un polígono regular es\(135^{\circ}\). ¿Cuántos lados tiene este polígono?
Solución
Aquí, estableceremos la Fórmula de Ángulo Interior Polígono Regular igual\(135^{\circ}\) y resolveremos para n.
\(\begin{aligned} \dfrac{(n−2)\times 180^{\circ}}{n}&=135^{\circ} \\ 180^{\circ}n−360^{\circ}−360^{\circ}&=135^{\circ}n \\ n&=−45^{\circ} \\ n&=8\qquad \text{The polygon is an octagon.} \end{aligned}\)
Revisar
- Rellene la tabla.
| # de lados | Suma de los ángulos interiores | Medida de cada ángulo interior en un n−gon regular |
|---|---|---|
| 3 | \(60^{\circ}\) | |
| 4 | \(360^{\circ}\) | |
| 5 | \(540^{\circ}\) | \(108^{\circ}\) |
| 6 | \(120^{\circ}\) | |
| 7 | ||
| 8 | ||
| 9 | ||
| 10 | ||
| 11 | ||
| 12 |
- ¿Cuál es la suma de los ángulos en un 15 gon?
- ¿Cuál es la suma de los ángulos en un 23-gon?
- La suma de los ángulos interiores de un polígono es\(4320^{\circ}\). ¿Cuántos lados tiene el polígono?
- La suma de los ángulos interiores de un polígono es\(3240^{\circ}\). ¿Cuántos lados tiene el polígono?
- ¿Cuál es la medida de cada ángulo en un 16 gon regular?
- ¿Cuál es la medida de cada ángulo en un equiangular de 24 gones?
- Cada ángulo interior en un polígono regular es\(156^{\circ}\). ¿Cuántos lados tiene?
- Cada ángulo interior en un polígono equiangular es\(90^{\circ}\). ¿Cuántos lados tiene?
Para las preguntas 10-18, encuentre el valor de las variables faltantes.
-
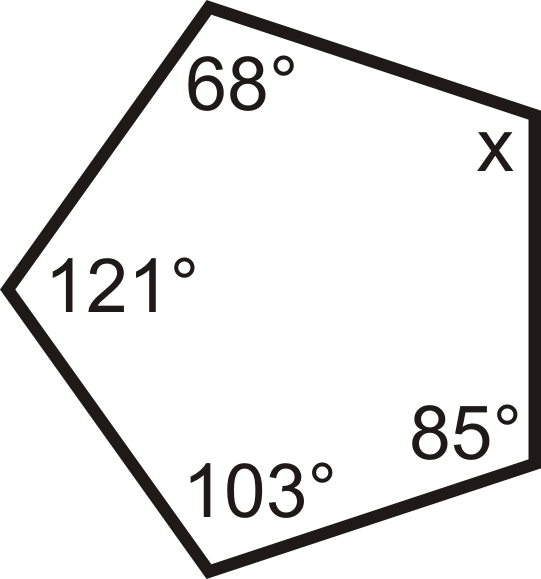
Figura\(\PageIndex{5}\) -
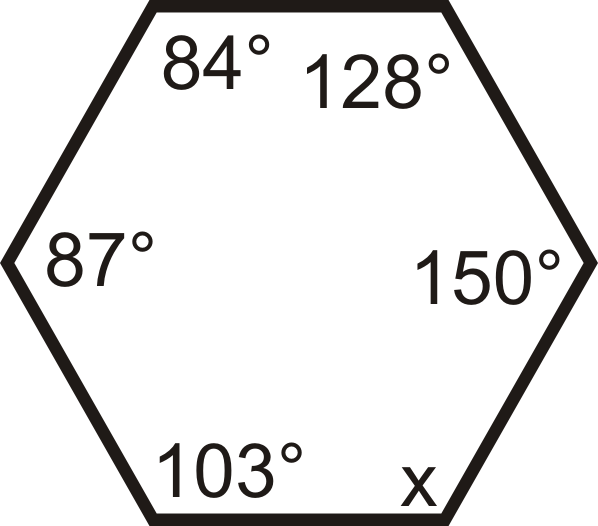
Figura\(\PageIndex{6}\) -
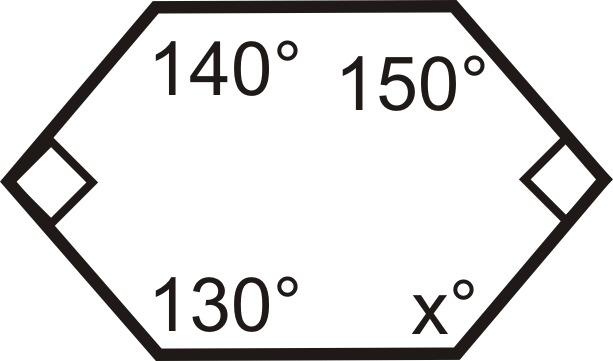
Figura\(\PageIndex{7}\) -
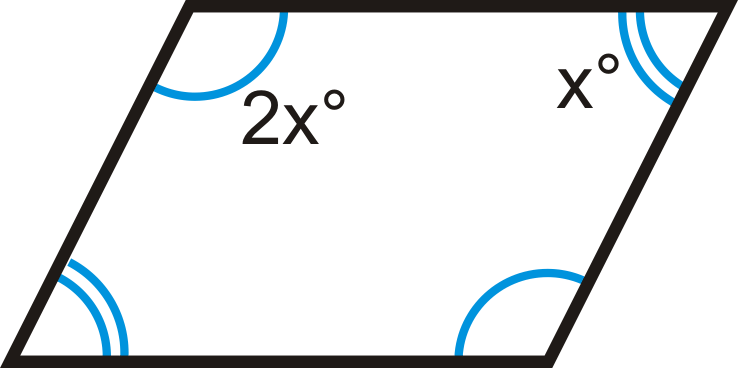
Figura\(\PageIndex{8}\) -
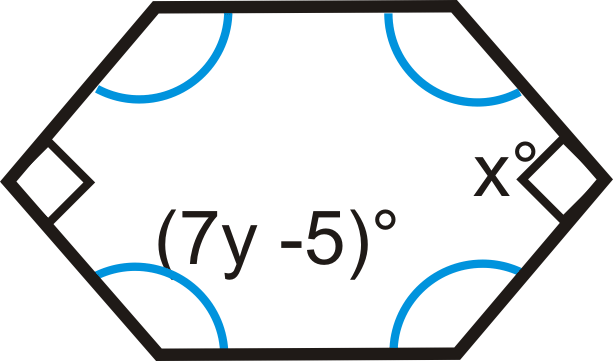
Figura\(\PageIndex{9}\) -
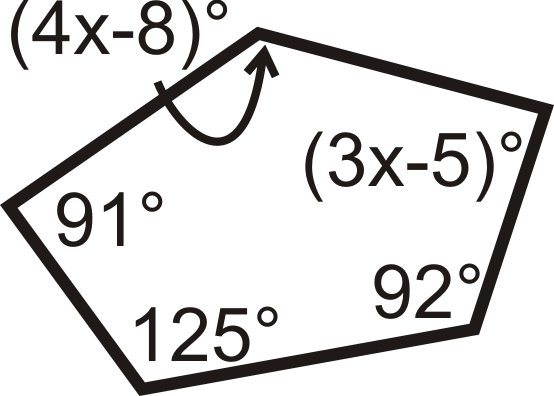
Figura\(\PageIndex{10}\) -
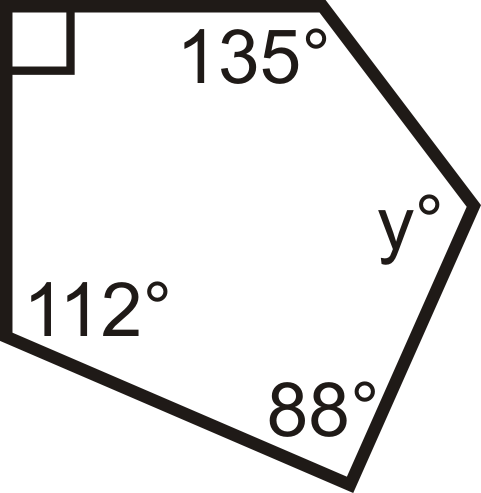
Figura\(\PageIndex{11}\) -
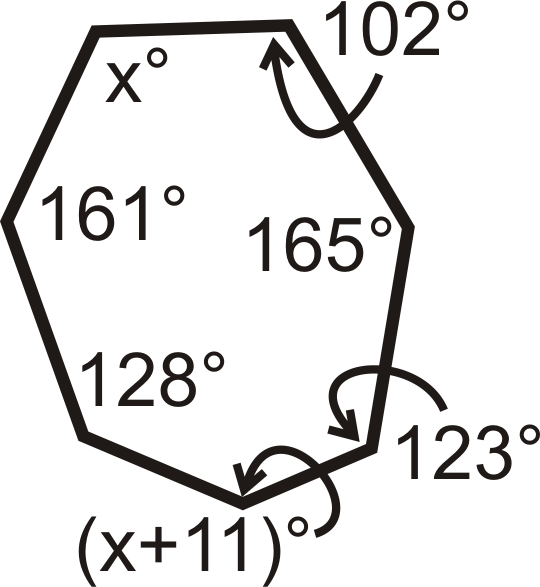
Figura\(\PageIndex{12}\) -
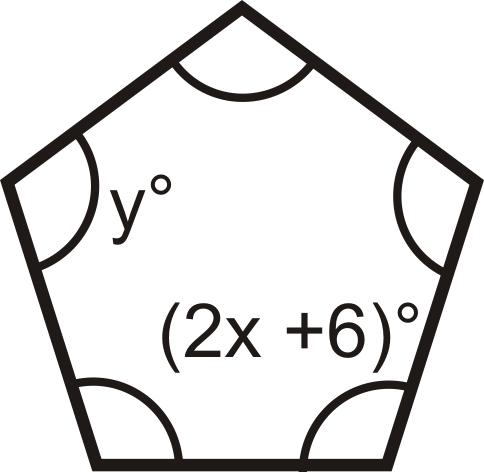
Figura\(\PageIndex{13}\)
- Los ángulos interiores de un hexágono son\(x^{\circ}\)\((x+1)^{\circ}\),\((x+2)^{\circ}\),\((x+3)^{\circ}\),\((x+4)^{\circ}\), y\((x+5)^{\circ}\). ¿Qué es\(x\)?
Reseña (Respuestas)
Para ver las respuestas de Revisar, abra este archivo PDF y busque la sección 6.1.
Recursos
El vocabulario
| Término | Definición |
|---|---|
| Ángulos interiores | Los ángulos interiores son los ángulos dentro de una figura. |
| Fórmula de suma de polígonos | La fórmula de suma de polígonos establece que para cualquier polígono con n lados, los ángulos interiores suman\((n−2)\times 180\) grados. |
Recursos adicionales
Elemento Interactivo
Video: Ángulos interiores y exteriores de un polígono
Actividades: Ángulos interiores en polígonos convexos Preguntas de discusión
Ayudas de estudio: Guía de estudio de polígonos
Práctica: Ángulos interiores en polígonos convexos
Mundo real: ángulos interiores en polígonos convexos