5.28: Ángulos exteriores en polígonos convexos
- Page ID
- 107542
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Medida de ángulos en el exterior de un polígono formado extendiendo un lado.
Teorema de la suma de ángulos exteriores
Un ángulo exterior es un ángulo que se forma extendiendo un lado del polígono.
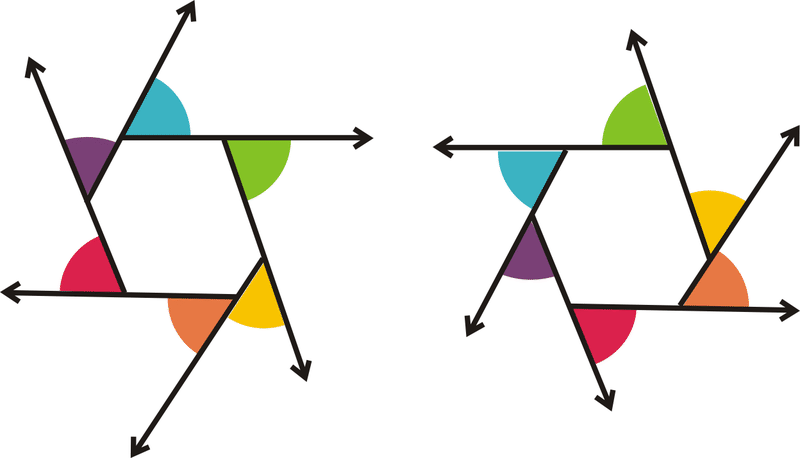
Como puede ver, hay dos conjuntos de ángulos exteriores para cualquier vértice en un polígono, uno que va alrededor de las agujas del reloj (1er hexágono) y el otro en sentido antihorario (2º hexágono). Los ángulos con los mismos colores son verticales y congruentes.
El Teorema de la Suma de Ángulo Exterior establece que la suma de los ángulos exteriores de CUALQUIER polígono convexo es\(360^{\circ}\). Si el polígono es regular con n lados, esto significa que cada ángulo exterior es\(\dfrac{360^{\circ}}{n}\).
¿Y si te dieran un polígono regular de siete lados? ¿Cómo se podría determinar la medida de cada uno de sus ángulos exteriores?
Ejemplo\(\PageIndex{1}\)
¿Cuál es la medida de cada ángulo exterior de un 12 gon regular?
Solución
Dividir\(360^{\circ}\) por el número dado de lados.
\(30^{\circ}\)
Ejemplo\(\PageIndex{2}\)
¿Cuál es la medida de cada ángulo exterior de un 100-gon regular?
Solución
Dividir\(360^{\circ}\) por el número dado de lados.
\(3.6^{\circ}\)
Ejemplo\(\PageIndex{3}\)
¿Qué es y?
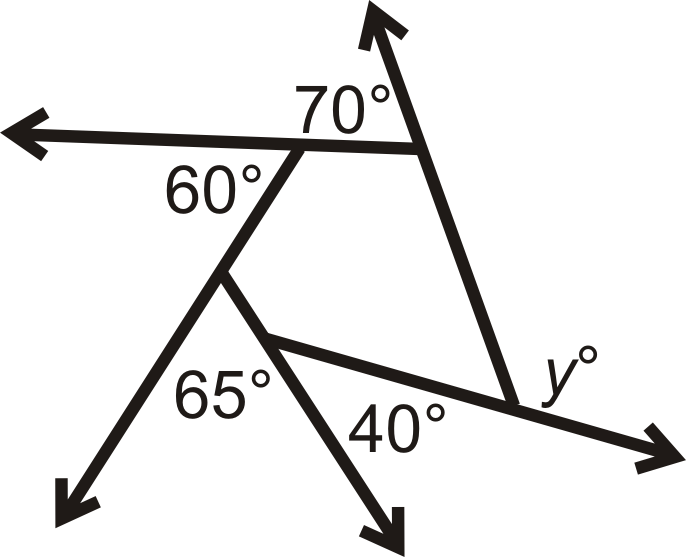
Solución
\(y\)es un ángulo exterior y todos los ángulos dados se suman a\(360^{\circ}\). Establecer una ecuación.
\(\begin{aligned} 70^{\circ}+60^{\circ}+65^{\circ}+40^{\circ}+y&=360^{\circ} \\ y&=125^{\circ} \end{aligned}\)
Ejemplo\(\PageIndex{4}\)
¿Cuál es la medida de cada ángulo exterior de un heptágono regular?
Solución
Debido a que el polígono es regular, los ángulos interiores son iguales. También significa que los ángulos exteriores son iguales. \(\dfrac{360^{\circ}}{7}\approx 51.43^{\circ}\)
Ejemplo\(\PageIndex{5}\)
¿Cuál es la suma de los ángulos exteriores en un 15 gon regular?
Solución
La suma de los ángulos exteriores en cualquier polígono convexo, incluyendo un 15 gon regular, es\(360^{\circ}\).
Revisar
- ¿Cuál es la medida de cada ángulo exterior de un decagón regular?
- ¿Cuál es la medida de cada ángulo exterior de un 30-gon regular?
- ¿Cuál es la suma de los ángulos exteriores de un 27-gon regular?
Encuentra la medida de las variables faltantes:
-
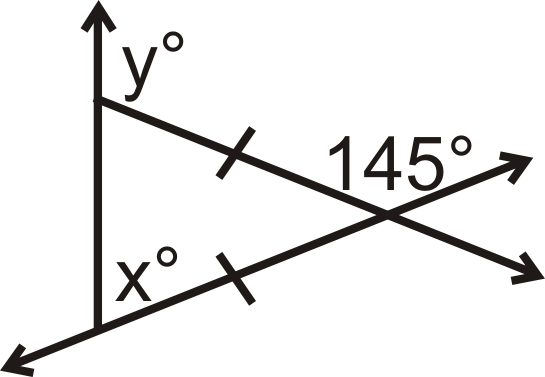
Figura\(\PageIndex{3}\) -
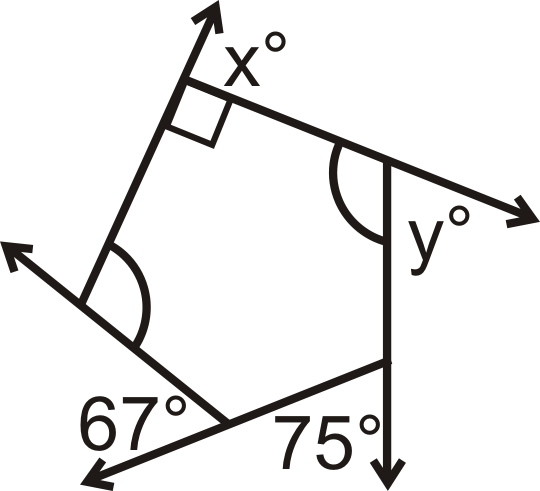
Figura\(\PageIndex{4}\)
- Los ángulos exteriores de un cuadrilátero son\(x^{\circ}\),\(2x^{\circ}\),\(3x^{\circ}\), y\(4x^{\circ}\). ¿Qué es\(x\)?
Encuentre la medida de cada ángulo exterior para cada polígono regular a continuación:
- octágono
- nonagon
- triángulo
- pentágono
Reseña (Respuestas)
Para ver las respuestas de Revisar, abra este archivo PDF y busque la sección 6.2.
Recursos
El vocabulario
| Término | Definición |
|---|---|
| ángulo exterior | Un ángulo que se forma extendiendo un lado del polígono. |
| polígono regular | Polígono en el que todos sus lados y todos sus ángulos son congruentes. |
| Teorema de la suma de ángulos exteriores | El teorema de la suma de ángulos exteriores establece que los ángulos exteriores de cualquier polígono siempre sumarán 360 grados. |
Recursos adicionales
Elemento interactivo
Video: Ángulos interiores y exteriores de un polígono
Actividades: Ángulos exteriores en polígonos convexos Preguntas de discusión
Ayudas de estudio: Guía de estudio de polígonos
Mundo real: Teorema de ángulos exteriores