8.5: Traducción Geométrica
- Page ID
- 107617
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Entender las traducciones como movimiento de cada punto de una figura a la misma distancia en la misma dirección. Graficar imágenes dadas preimagen y traducción.
Traducciones
Una transformación es una operación que mueve, voltea o cambia de otra manera una figura para crear una nueva figura. Una transformación rígida (también conocida como transformación de isometría o congruencia) es una transformación que no cambia el tamaño o la forma de una figura.
Las transformaciones rígidas son traslaciones, reflexiones y rotaciones. La nueva figura creada por una transformación se llama la imagen. La figura original se llama la preimagen. Si la preimagen es\(A\), entonces la imagen sería\(A′\), dijo “un primo”. Si hay una imagen de\(A′\), eso sería etiquetado\(A′′\), dijo “un doble primo”.
Una traslación es una transformación que mueve cada punto de una figura a la misma distancia en la misma dirección. Por ejemplo, esta transformación mueve el paralelogramo hacia la derecha 5 unidades y hasta 3 unidades. Está escrito\((x,y)\rightarrow (x+5, y+3)\).
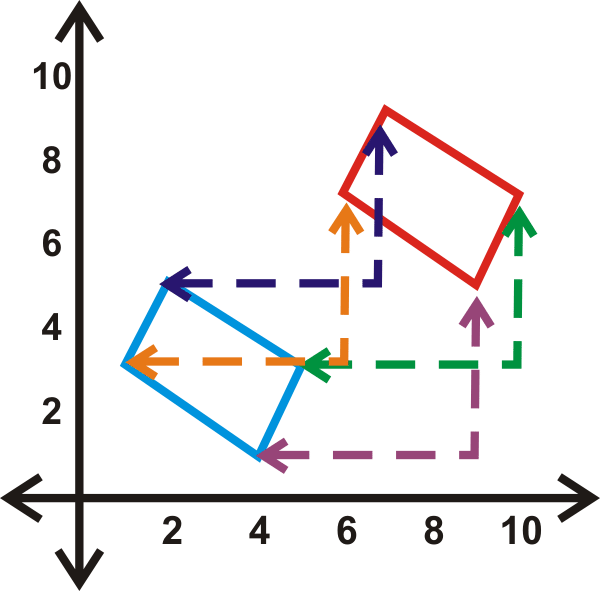
¿Y si te dieran las coordenadas de un cuadrilátero y te pidieran mover ese cuadrilátero 3 unidades a la izquierda y 2 unidades hacia abajo? ¿Cuáles serían sus nuevas coordenadas?
Ejemplo\(\PageIndex{1}\)
Triángulo\(\Delta ABC\) tiene coordenadas\(A(3,−1)\),\(B(7,−5)\) y\(C(−2,−2)\). Traducir\(\Delta ABC\) a la izquierda 4 unidades y hasta 5 unidades. Determinar las coordenadas de\(\Delta A′B′C′\).
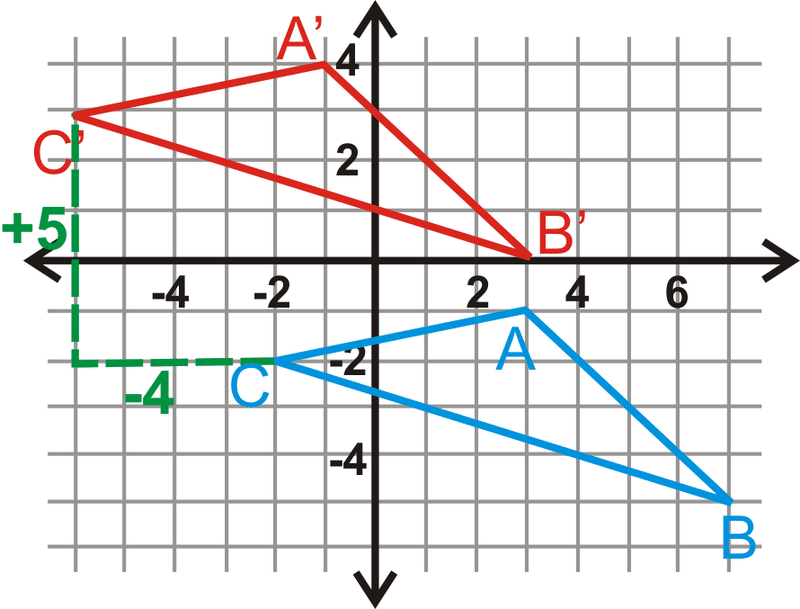
Solución
Gráfica\(\Delta ABC\). Para traducir\(\Delta ABC\), restar 4 de cada\(x\) valor y sumar 5 a cada\(y\) valor de sus coordenadas.
\(\begin{aligned} &A(3,−1)\rightarrow (3−4,−1+5)=A′(−1,4) \\ &B(7,−5)\rightarrow (7−4,−5+5)=B′(3,0) \\ &C(−2,−2)\rightarrow (−2−4,−2+5)=C′(−6,3) \end{aligned}\)
La regla sería\((x,y)\rightarrow (x−4, y+5)\).
Ejemplo\(\PageIndex{2}\)
Usando la traducción\((x,y)\rightarrow (x+2, y−5)\), ¿cuál es la imagen\(A(−6, 3)\)?
Solución
\(A′(−4,−2)\)
Ejemplo\(\PageIndex{3}\)
Gráfica cuadrada\(S(1,2)\),\(Q(4,1)\),\(R(5,4)\) y\(E(2,5)\). Encuentra la imagen después de la traducción\((x,y)\rightarrow (x−2,y+3)\). Después, grafica y etiqueta la imagen.
Solución
Vamos a mover la plaza a la izquierda 2 y arriba 3.
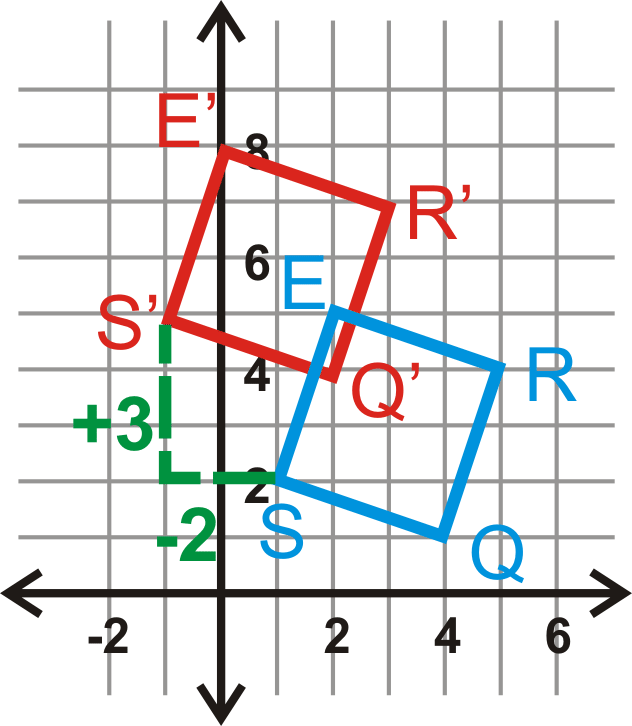
\(\begin{aligned}(x,y)&\rightarrow (x−2,y+3) \\ S(1,2)&\rightarrow S′(−1,5) \\ Q(4,1)&\rightarrow Q′(2,4) \\ R(5,4)&\rightarrow R′(3,7) \\ E(2,5)&\rightarrow E′(0,8)\end{aligned}\)
Ejemplo\(\PageIndex{4}\)
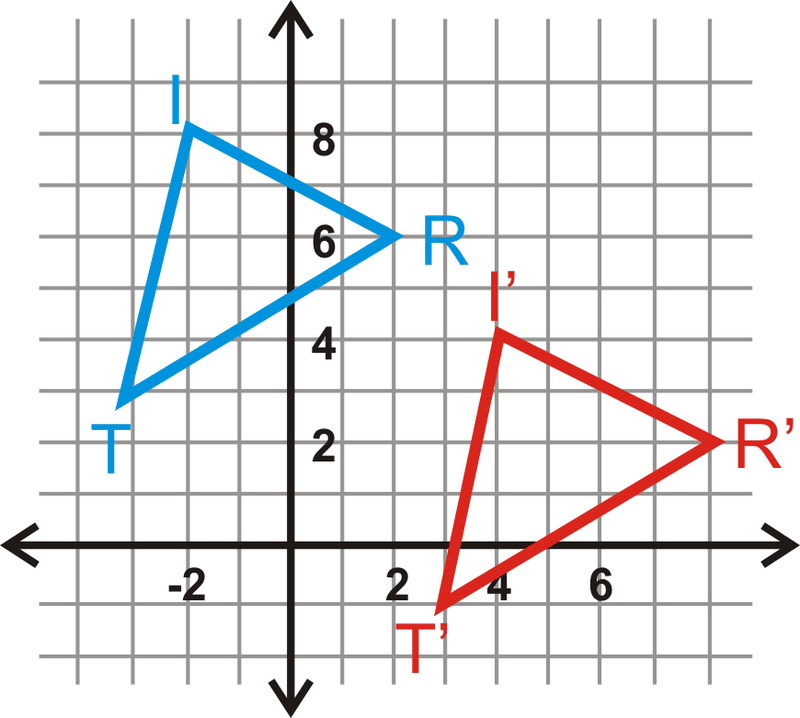
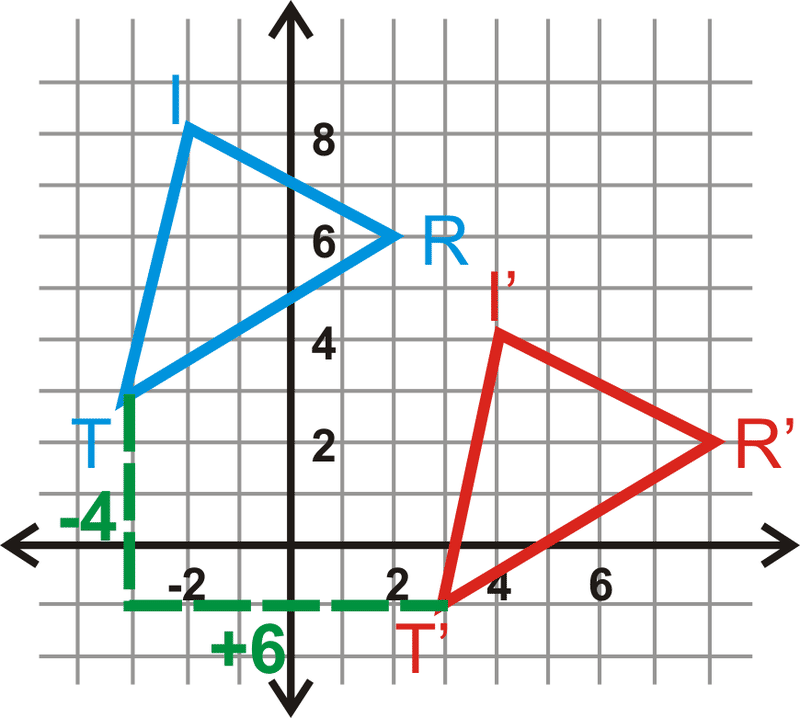
Encuentra la regla de traducción para\(\Delta TRI\) a\(\Delta T′R′I′\).
Solución
Mira el movimiento de\(T\) a\(T′\). La regla de traducción es\((x,y)\rightarrow (x+6, y−4)\).
Revisar
Utilice la traducción\((x,y)\rightarrow (x+5, y−9)\) para las preguntas 1-7.
- ¿De qué es la imagen\(A(−1,3)\)?
- ¿De qué es la imagen\(B(2,5)\)?
- ¿De qué es la imagen\(C(4,−2)\)?
- ¿De qué es la imagen\(A′\)?
- ¿Cuál es la preimagen de\(D′(12,7)\)?
- ¿De qué es la imagen\(A′′\)?
- Trama\(A\),\(A′\),\(A′′\), y\(A′′′\) a partir de las preguntas anteriores. ¿Qué notas?
Los vértices de\(\Delta ABC\) son\(A(−6,−7)\),\(B(−3,−10)\) y\(C(−5,2)\). Encuentra los vértices de\(\Delta A′B′C′\), dadas las reglas de traducción a continuación.
- \((x,y)\rightarrow (x−2, y−7)\)
- \((x,y)\rightarrow (x+11, y+4)\)
- \((x,y)\rightarrow (x, y−3)\)
- \((x,y)\rightarrow (x−5, y+8)\)
- \((x,y)\rightarrow (x+1, y)\)
- \((x,y)\rightarrow (x+3, y+10)\)
En las preguntas 14-17,\(\Delta A′B′C′\) es la imagen de\(\Delta ABC\). Escribe la regla de traducción.
-
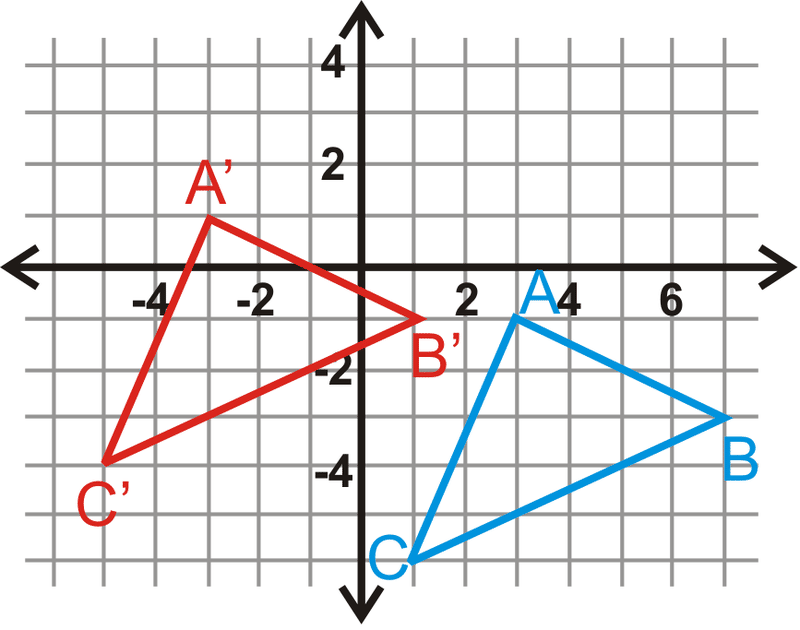
Figura\(\PageIndex{6}\) -
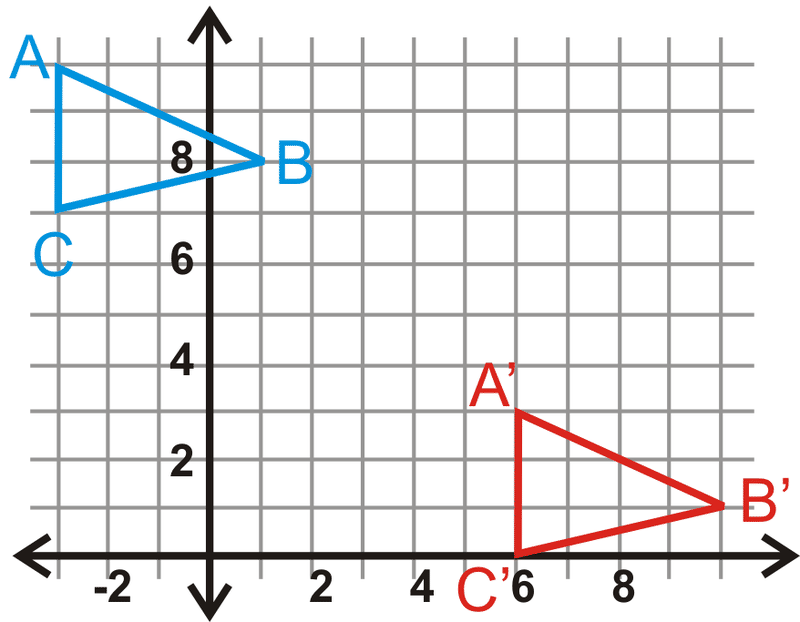
Figura\(\PageIndex{7}\) -
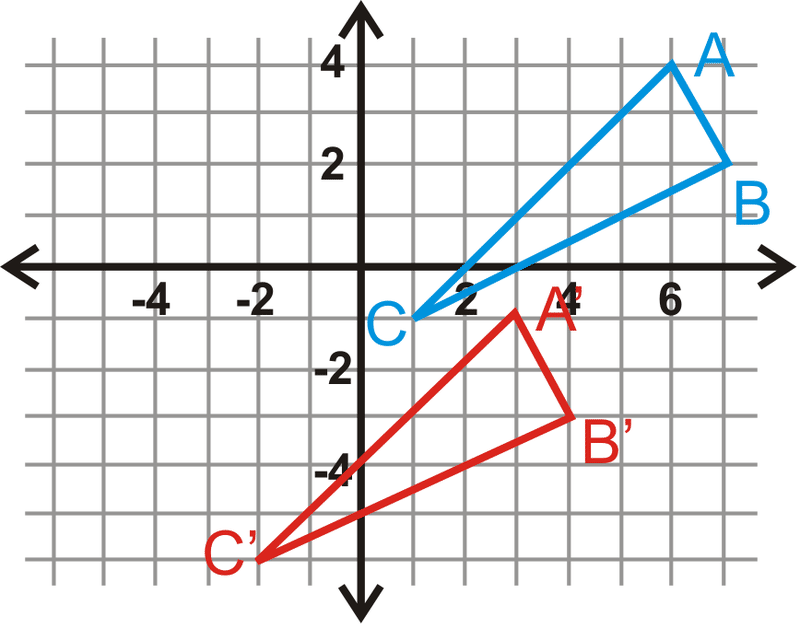
Figura\(\PageIndex{8}\) -
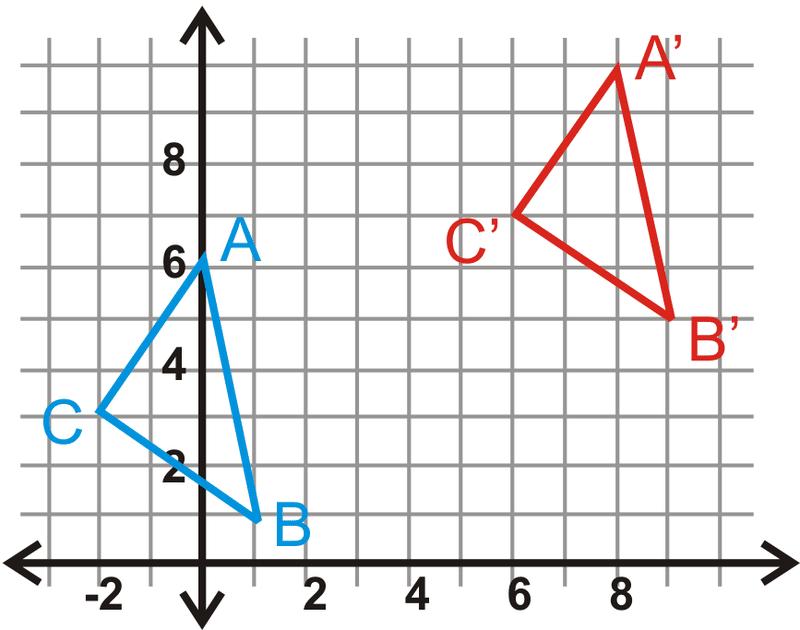
Figura\(\PageIndex{9}\)
Usa los triángulos de #17 para responder a las preguntas 18-20.
- Encuentra las longitudes de todos los lados de\(\Delta ABC\).
- Encuentra las longitudes de todos los lados de\(\Delta A′B′C′\).
- ¿Qué puedes decir sobre\(\Delta ABC\) y\(\Delta A′B′C′\)? ¿Puedes decir esto para alguna traducción?
- Si\(\Delta A′B′C′\) era la preimagen y\(\Delta ABC\) era la imagen, escribe la regla de traducción para #14.
- Si\(\Delta A′B′C′\) era la preimagen y\(\Delta ABC\) era la imagen, escribe la regla de traducción para #15.
- Encuentra la regla de traducción\(A\) a la que se movería\(A′(0,0)\), para #16.
- Las coordenadas de\(\Delta DEF\) son\(D(4,−2)\),\(E(7,−4)\) y\(F(5,3)\). Traducir\(\Delta DEF\) a la derecha 5 unidades y hasta 11 unidades. Escribe la regla de traducción.
- Las coordenadas del cuadrilátero\(QUAD\) son\(Q(−6,1)\),\(U(−3,7)\),\(A(4,−2)\) y\(D(1,−8)\). Traducir\(QUAD\) a la izquierda 3 unidades y abajo 7 unidades. Escribe la regla de traducción.
Reseña (Respuestas)
Para ver las respuestas de Revisar, abra este archivo PDF y busque la sección 12.3.
Recursos adicionales
Elemento Interactivo
Video: Transformación: Principios de traducción - Básico
Actividades: Traducciones Preguntas de discusión
Ayudas de estudio: Guía de estudio de tipos de transformaciones
Práctica: Traducción Geométrica