8.4: Simetría de rotación
- Page ID
- 107628
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Rotación inferior a 360 grados que lleva una forma sobre sí misma.
La simetría rotacional está presente cuando una figura se puede girar (menos que\(360^{\circ}\)) de tal manera que parece que lo hizo antes de la rotación. El centro de rotación es el punto alrededor del cual se gira una figura de tal manera que se mantiene la simetría rotacional.
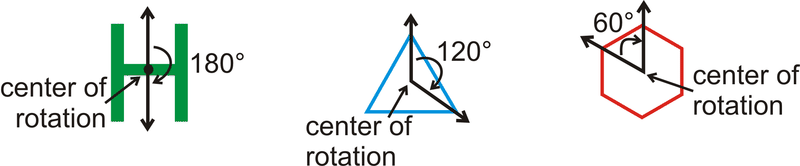
Para el\(H\), podemos girarlo dos veces, el triángulo puede girarse 3 veces y aún así verse igual y el hexágono se puede girar 6 veces.
¿Y si tuvieras una estrella de seis puntas y giraras esa estrella menos de\(360^{\circ}\)? Si la estrella rotada se veía exactamente igual que la estrella original, ¿qué diría eso de la estrella?
Ejemplo\(\PageIndex{1}\)
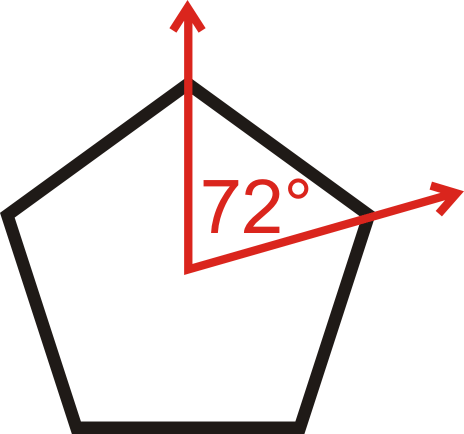
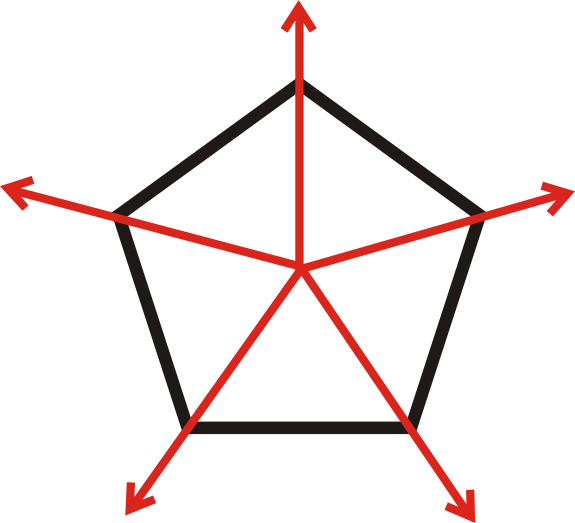
Determinar si la siguiente figura tiene simetría rotacional. Encuentra el ángulo y cuántas veces se puede girar.
Solución
El pentágono se puede girar 5 veces. Debido a que hay 5 líneas de simetría rotacional, el ángulo sería\(\dfrac{360^{\circ}}{5}=72^{\circ}\).
Ejemplo\(\PageIndex{2}\)
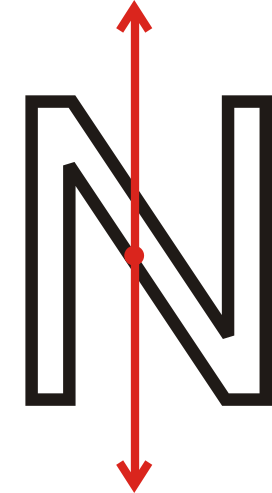
Determinar si la siguiente figura tiene simetría rotacional. Encuentra el ángulo y cuántas veces se puede girar.
Solución
El N se puede girar dos veces. Esto significa que el ángulo de rotación es\(180^{\circ}\).
Ejemplo\(\PageIndex{3}\)
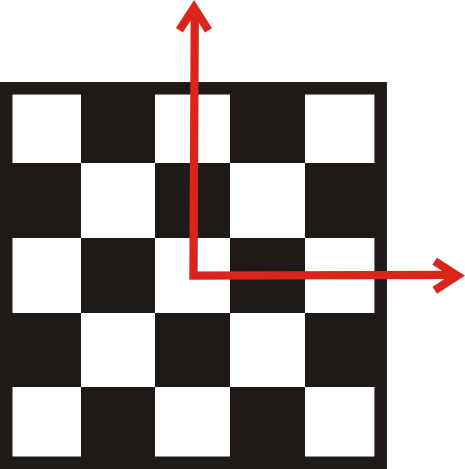
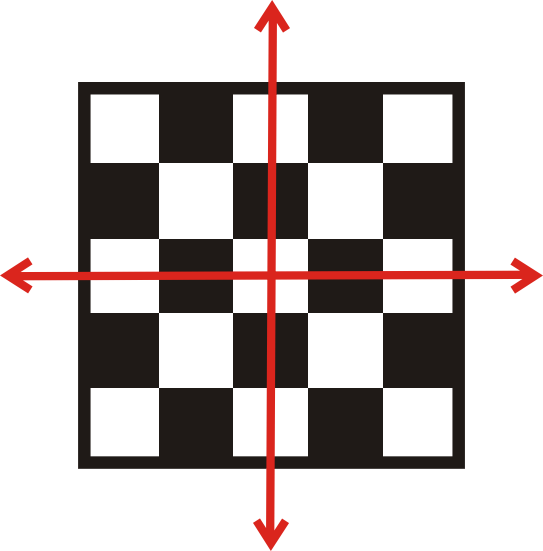
Determinar si la siguiente figura tiene simetría rotacional. Encuentra el ángulo y cuántas veces se puede girar.
Solución
El tablero de ajedrez se puede girar 4 veces. Hay 4 líneas de simetría rotacional, por lo que el ángulo de rotación es\(\dfrac{360^{\circ}}{4}=90^{\circ}\).
Ejemplo\(\PageIndex{4}\)
Encuentra el ángulo de rotación y el número de veces que cada figura puede girar.
Solución
El paralelogramo se puede girar dos veces. El ángulo de rotación es\(180^{\circ}\).
Ejemplo\(\PageIndex{5}\)
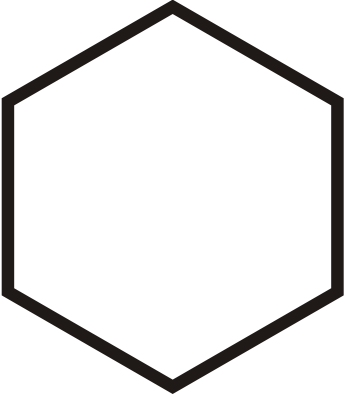
Solución
El hexágono se puede girar seis veces. El ángulo de rotación es\(60^{\circ}\).
Revisar
- Si una figura tiene 3 líneas de simetría rotacional, se puede girar _______ veces.
- Si una figura se puede rotar 6 veces, tiene _______ líneas de simetría rotacional.
- Si una figura se puede girar n veces, tiene _______ líneas de simetría rotacional.
- Para encontrar el ángulo de rotación, divídalo\(360^{\circ}\) por el número total de _____________.
- Cada cuadrado tiene un ángulo de rotación de _________.
Determinar si cada declaración es verdadera o falsa.
- Cada paralelogramo tiene simetría rotacional.
- Cada figura que tiene simetría lineal también tiene simetría rotacional.
Determinar si las siguientes palabras tienen simetría de rotación.
- OHIO
- MOW
- WOW
- KICK
- pod
Encuentra el ángulo de rotación y el número de veces que cada figura puede girar.
-
Figura\(\PageIndex{12}\) -
Figura\(\PageIndex{13}\) -
Figura\(\PageIndex{14}\)
Determinar si las figuras a continuación tienen simetría de rotación. Identificar el ángulo de rotación.
-
Figura\(\PageIndex{15}\) -
Figura\(\PageIndex{16}\) -
Figura\(\PageIndex{17}\)
Reseña (Respuestas)
Para ver las respuestas de Revisar, abra este archivo PDF y busque la sección 12.2.
El vocabulario
| Término | Definición |
|---|---|
| simetría rotacional | Cuando una figura se puede rotar (menos de 360^ {\ circ}\)) tal que parece que lo hacía antes de la rotación. El centro de rotación es el punto alrededor del cual se gira una figura de tal manera que se mantiene la simetría rotacional. |
| Centro de Rotación | En una rotación, el centro de rotación es el punto que no se mueve. El resto del plano gira alrededor de este punto fijo. |
| Rotación | Una rotación es una transformación que convierte una figura en el plano de coordenadas un cierto número de grados alrededor de un punto dado sin cambiar la forma o el tamaño de la figura. |
| Simetría de rotación | Una figura tiene simetría rotacional si se puede girar menos que\(360^{\circ}\) alrededor de su punto central y se ve exactamente igual que antes de la rotación. |
| Simetría | Una figura tiene simetría si se puede transformar y seguir pareciendo igual. |
Recursos adicionales
Elemento Interactivo
Video: Principios de simetría de rotación - Básico
Actividades: Rotación Simetría Discusión Preguntas
Ayudas de estudio: Guía de estudio de simetría y teselaciones
Práctica: Simetría de rotación
Mundo Real: Esto Termina