8.6: Figuras deslizantes
- Page ID
- 107600
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\(\newcommand{\longvect}{\overrightarrow}\)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Utilice coordenadas para mover figuras en el plano de coordenadas.
Clasificación de Transformación

La señora Gilcrest ha diseñado una versión especial del juego Battleship. Su versión requiere que los estudiantes utilicen coordenadas como (1, 2) para adivinar la ubicación de un barco. Las naves están estratégicamente colocadas para que cada una sea una traslación de la otra. Para que el juego sea más fácil para los alumnos, tradujo los barcos a la misma distancia arriba o abajo, derecha o izquierda. Si el primer barco está en (3, 6), (3, 7), (3, 8) y el segundo barco se traslada 4 unidades a la derecha y 4 unidades hacia arriba, ¿cuáles son las coordenadas del segundo barco?
En este concepto, aprenderás a clasificar las transformaciones.
Clasificación de Transformaciones
El plano de coordenadas es una representación del espacio bidimensional. Tiene un eje horizontal, llamado eje\(x\) -eje, y un eje vertical, llamado\(y\) eje -eje. Puede graficar y mover figuras geométricas en el plano de coordenadas.
Recuerda los tres tipos de transformaciones: la traslación, la reflexión y la rotación.
Ahora veamos cómo realizar cada tipo de transformación en el plano de coordenadas.
Cuando realizas traducciones, deslizas una figura hacia la izquierda o hacia la derecha, hacia arriba o hacia abajo. Esto significa que en el plano de coordenadas, las coordenadas para los vértices de la figura cambiarán. Echa un vistazo al ejemplo a continuación.
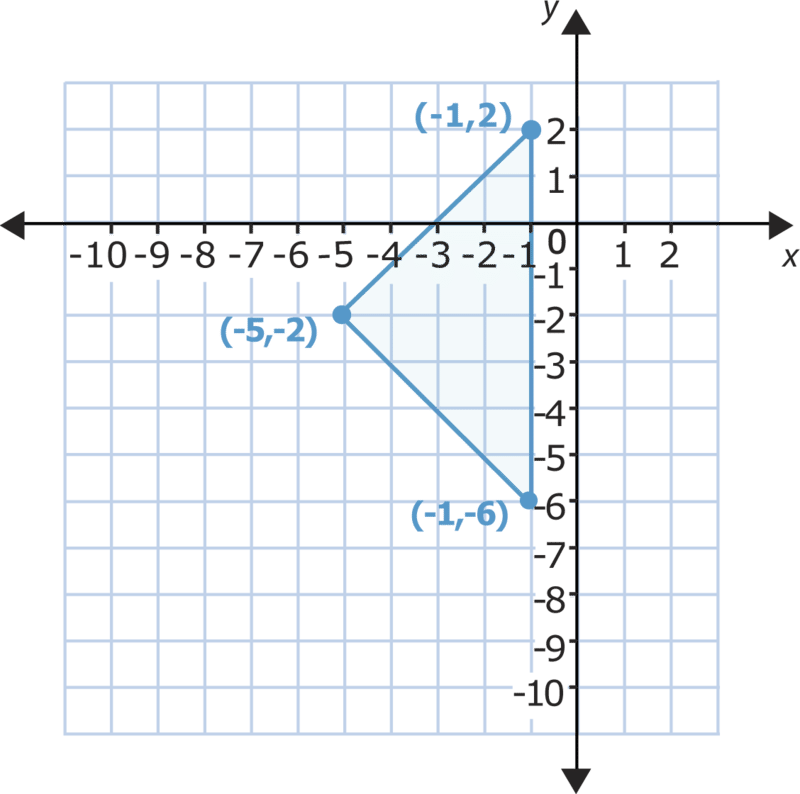
Ahora veamos realizar una traducción o diapositiva de esta figura.
Puedes elegir el número de lugares en los que quieres mover el triángulo y la dirección en la que deseas moverlo. Si deslizas este triángulo 3 lugares hacia abajo, todos sus vértices desplazarán 3 lugares hacia abajo del\(y\) eje -y la\(y\) coordenada -en cada par disminuirá en 3.
Veamos por qué sucede esto.
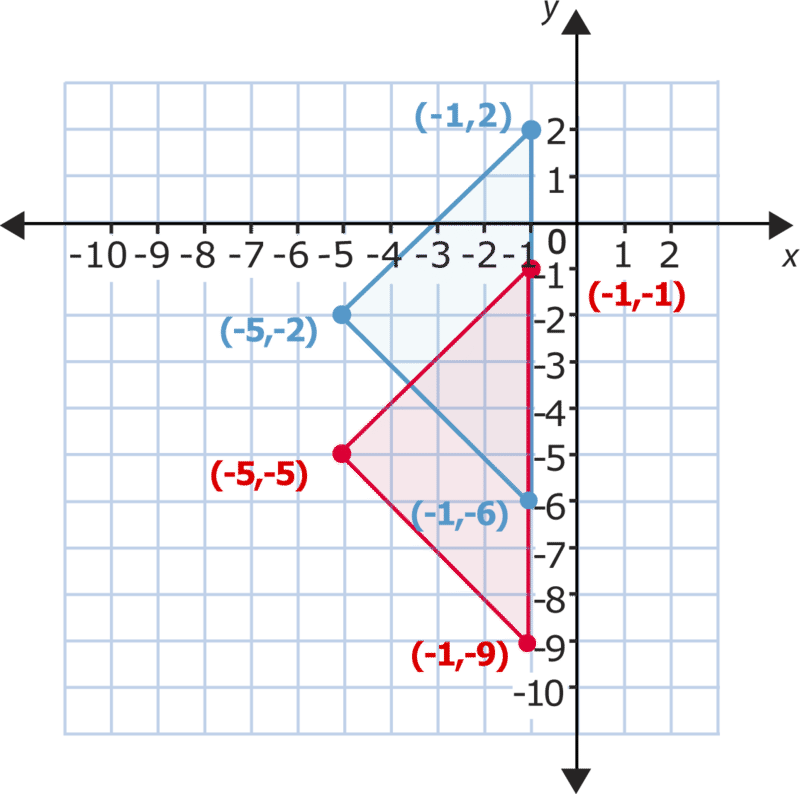
Se puede ver el cambio en todas las\(y\) coordenadas. Compara los puntos más altos. La\(y\) coordenada -a la izquierda es 2. La\(y\) coordenada -para el punto correspondiente en el triángulo después de que se mueva es -1. La\(y\) coordenada -disminuye en 3. Ahora compara el punto izquierdo de cada triángulo. La\(y\) coordenada -originalmente es -2, y la\(y\) coordenada -después de la traslación es -5. Nuevamente, la diferencia muestra un cambio de -3 en la\(y\) coordenada. Para el último punto, la\(y\) coordenada -comienza como -6, y cambia a -9 después del deslizamiento hacia abajo. Para cada punto, la\(y\) coordenada -disminuye en 3 mientras que las\(x\) coordenadas -permanecen iguales.
También se pueden traducir cifras de otras formas. Como puede adivinar, mueve las figuras a la derecha o a la izquierda en la cuadrícula de coordenadas por sus\(x\) coordenadas. También puedes mover figuras diagonalmente cambiando sus coordenadas x y\(y\) -coordenadas. Una forma de reconocer las traducciones, entonces, es comparar sus puntos. Todas las\(x\) coordenadas cambiarán de la misma manera, y las\(y\) coordenadas -cambiarán de la misma manera.
Aquí hay un ejemplo de cómo graficar una traducción.
Deslice la siguiente figura 5 lugares a la derecha.
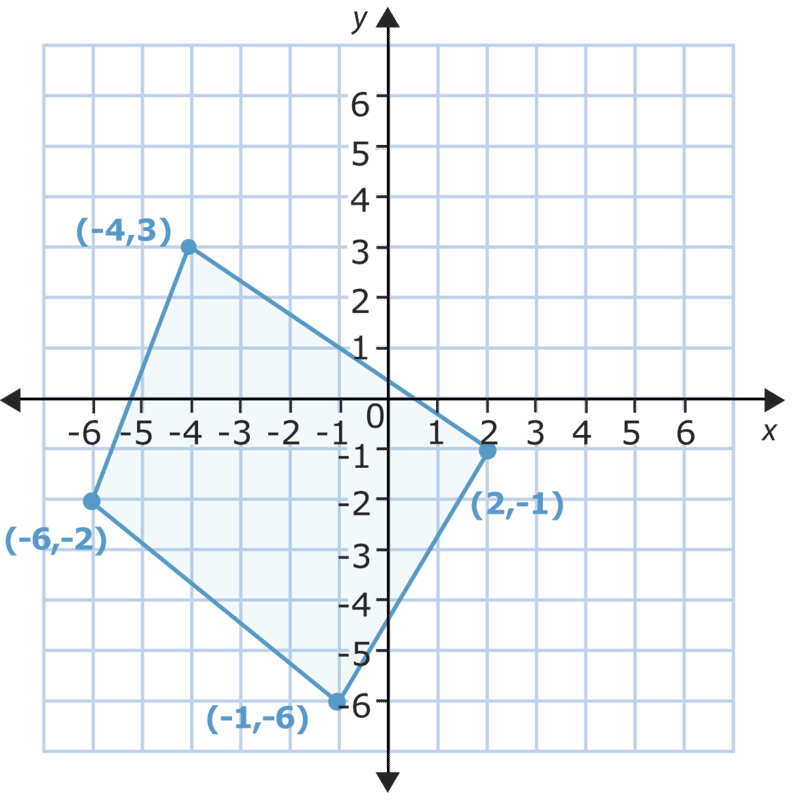
En esta traducción, moverás la figura hacia la derecha. Eso significa que las\(x\) coordenadas -para cada punto cambiarán pero las\(y\) coordenadas -no lo harán. Simplemente cuentas 5 lugares a la derecha de cada punto y haces un nuevo punto.
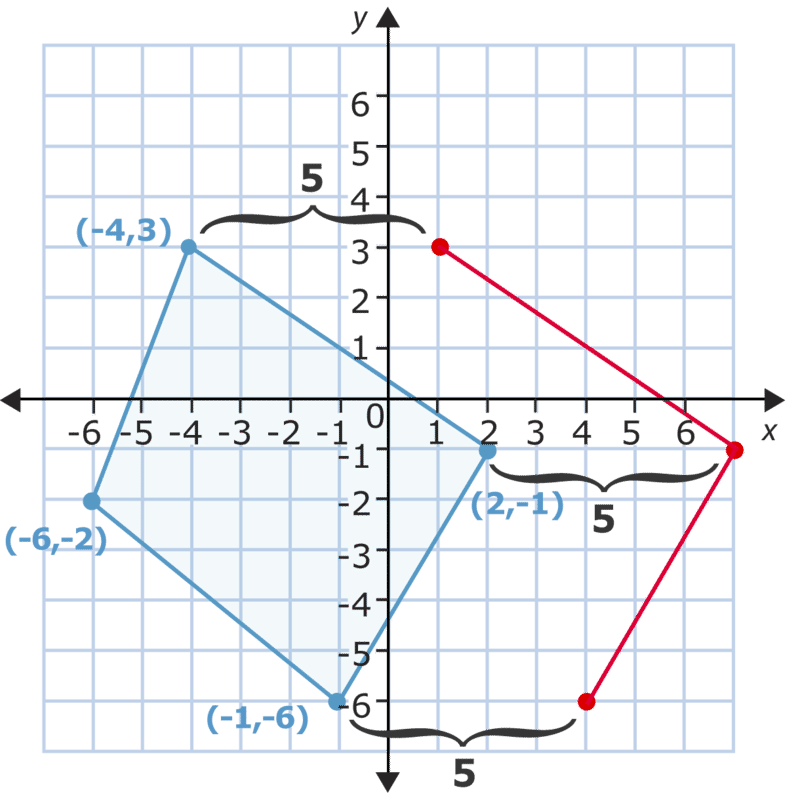
Una vez que reubica cada punto 5 lugares a la derecha, puede conectarlos para hacer la nueva figura que muestra la traducción.
Se puede verificar para ver si realizó la traducción correctamente agregando 5 a cada\(x\) coordenada (porque se movió hacia la derecha) y luego verificando estas contra los pares ordenados de la figura que dibujaste. Esto se llama notación de coordenadas. Observe que cada punto está representado por coordenadas.
\ (\ begin {array} {lccc}
(-4,3) & (-6, -2) & (-1, -6) & (2, -1)\\
+5 & +5 & +5 & +5\
(1,3) & (-1, -2) & (4, -6) & (7, -1)
\ end {array}\)
Estos son los puntos que graficaste, por lo que has realizado la traducción correctamente.
Ejemplo\(\PageIndex{1}\)
Anteriormente, se le dio un problema sobre la señora Gilcrest y su versión especial del juego Battleship.
Ella tradujo los barcos a la misma distancia arriba o abajo, derecha o izquierda. Si el primer barco está en (3, 6), (3, 7), (3, 8) y el segundo barco se traslada 4 unidades a la derecha y 4 unidades hacia arriba, ¿cuáles son las coordenadas del segundo barco?
Solución
Primero, recuerda los signos asociados con un movimiento hacia la derecha y un movimiento hacia arriba.
Derecha es un movimiento en la dirección positiva en el\(x\) eje -y hacia arriba es un movimiento en la dirección positiva en el\(y\) eje -eje.
A continuación, agregue los movimientos a las coordenadas.
(3+4, 6+4), (3+4, 7+4), (3+4, 8+4)
Luego escribe los nuevos vértices
(7, 10), (7, 11), (7, 12)
Las coordenadas de la segunda nave son (7, 10), (7, 11), (7, 12).
Ejemplo\(\PageIndex{2}\)
Resolver este problema.
Deslice la siguiente figura 4 lugares a la izquierda y 2 lugares hacia arriba.
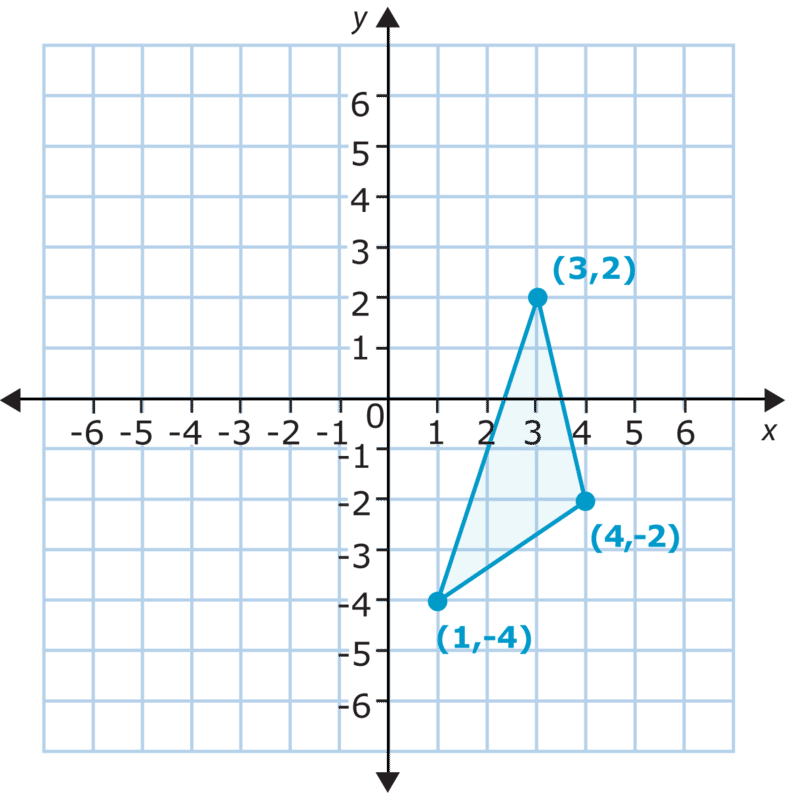
Solución
Primero, grafica los nuevos puntos.
Grafica cada punto contando 4 lugares a la izquierda, y de ahí 2 lugares hacia arriba.
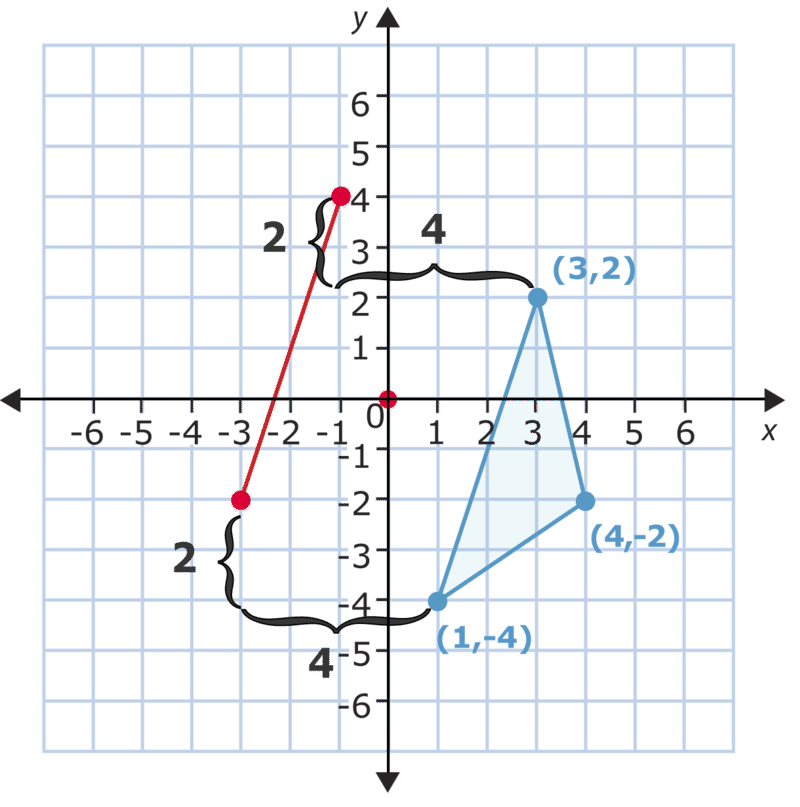
Entonces, formar el nuevo triángulo.
Conecta los nuevos puntos.
Puedes verificar la traducción cambiando las\(y\) coordenadas\(x\) - y -en los pares ordenados y luego comparándolas con los puntos que graficaste. Esta vez resta 4 de cada\(x\) coordenada y suma 2 a cada\(y\) coordenada. Veamos qué pasa.
\ (\ begin {array} {ccc}
(3,2) & (4, -2) & (1, -4)\\
-4+2 & -4+2 & -4+2\\
(-1,4) & (0,0) & (-3, -2)
\ end {array}\)
Ejemplo\(\PageIndex{3}\)
Traducir triángulo\(\(ABC\)\) (0, 1), (1, 3), (4, 0) arriba 4.
Solución
Primero, recuerda si arriba es un movimiento en el\(x\) eje -axis o el\(y\) -axis.
Arriba es un movimiento en el\(y\) eje.
A continuación, agregue 4 a cada uno de los\(y\) valores -.
(0, 1+4), (1, 3+4), (4, 0+4)
Después, escribe los nuevos vértices.
(0, 5), (1, 7), (4, 4)
El nuevo triángulo tiene coordenadas (0, 5), (1, 7), (4, 4).
Ejemplo\(\PageIndex{4}\)
Traducir Triángulo\(DEF\) (-3, 2), (1, 6), (2, 1) abajo 2.
Solución
Primero, recuerde si hacia abajo es un movimiento en el\(x\) eje -eje o en el\(y\) eje -eje.
Abajo es un movimiento en el\(y\) eje.
A continuación, resta 2 de cada uno de los\(y\) valores -.
(-3, 2-2), (1, 6-2), (2, 1-2)
Después, escribe los nuevos vértices.
(-3, 0), (1, 4), (2, -1)
El nuevo triángulo tiene coordenadas (-3, 0), (1, 4), (2, -1)
Ejemplo\(\PageIndex{5}\)
Traducir triángulo\(XYZ\) (-5, 4), (1, 8), (3, 5) a la derecha 3.
Solución
Primero, recuerde si la derecha es un movimiento en el\(x\) eje -eje o en el\(y\) eje -eje.
Derecha es un movimiento sobre el\(x\) eje.
A continuación, agregue 3 a cada\(x\) -valor.
(-5+3, 4), (1+3, 8), (3+3, 5)
Luego escribe los nuevos vértices
(-2, 4), (4, 8), (6, 5)
El nuevo triángulo tiene coordenadas (-2, 4), (4, 8), (6, 5).
Revisar
Identificar las transformaciones que se muestran a continuación como traslación, reflexión o rotación.

- Verdadero o falso. Esta cifra ha sido traducida 5 lugares a la derecha.
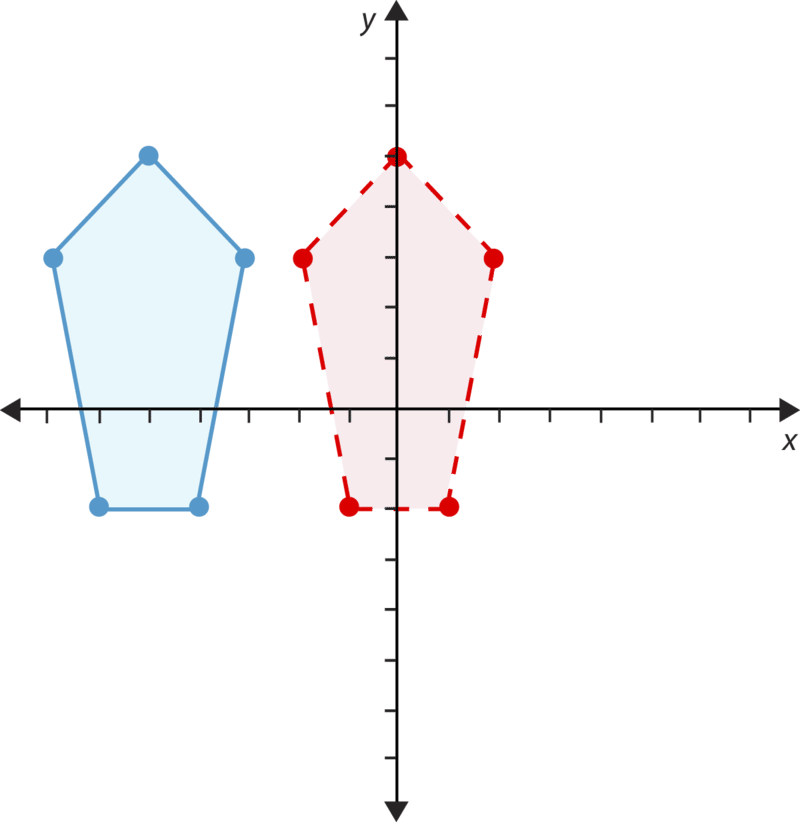
Traducir cada figura a la derecha 6 lugares y arriba 1. Después escribe las nuevas coordenadas para la figura.
- Triángulo\(DEF\) (-1, 2) (1, 6) (2, 1)
- Triángulo\(DEF\) (-3, 2) (1, 6) (2, 1)
- Triángulo\(DEF\) (0, 2) (1, 6) (2, 1)
- Triángulo\(DEF\) (4, -2) (1, 6) (2, 1)
- Triángulo\(DEF\) (5, 3) (1, 6) (2, 1)
- Triángulo\(DEF\) (4, 4) (1, 6) (2, 1)
Reseña (Respuestas)
Para ver las respuestas de Revisar, abra este archivo PDF y busque la sección 8.18.
Recursos
vocabulario
| Término | Definición |
|---|---|
| \(x\)-eje | El\(x\) eje -es el eje horizontal en el plano de coordenadas, que comúnmente representa el valor de la variable de entrada o independiente. |
| \(y\)-eje | El\(y\) eje -es la recta numérica vertical del plano cartesiano. |
| Plano de coordenadas | El plano de coordenadas es una rejilla formada por una recta numéricahorizontal y una recta numéricavertical que se cruzan en el punto (0, 0), denominado origen. El plano de coordenadas también se llama Plano Cartesiano. |
| Transformación | Una transformación mueve una figura de alguna manera en el plano de coordenadas. |
Recursos adicionales
Video: Identificar el cuadrante de un punto del sistema de coordenadas
Práctica: Figuras deslizantes

