8.8: Aplicaciones de traducción en similitud de círculo
- Page ID
- 107611
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Resolver problemas que involucran proporciones y círculos y usa transformaciones para mostrar que los círculos son similares.
Círculos y Similaridad
Sean tiene dos círculos, uno con un radio de 1 pulgada y otro con un radio de 3 pulgadas.
- ¿Cuál es la relación entre los radios de los círculos?
- ¿Cuál es el factor de escala entre los dos círculos?
- ¿Cuál es la relación entre las circunferencias de los círculos?
- ¿Cuál es la relación entre las áreas de los círculos?
- ¿Qué tienen que ver las relaciones de área y las proporciones de circunferencia con el factor de escala?
Un círculo es un conjunto de puntos equidistantes de un punto dado. El radio de un círculo, r, es la distancia desde el centro del círculo hasta el círculo. El tamaño de un círculo depende únicamente de su radio.
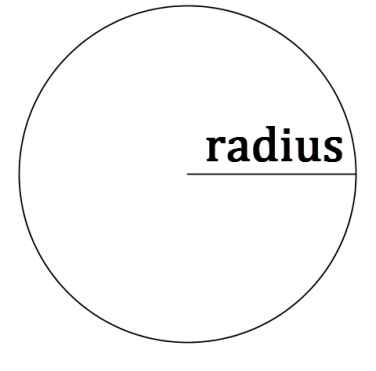
Dos figuras son similares si una transformación de similitud llevará una figura a la otra. Una transformación de similitud es una o más transformaciones rígidas seguidas de una dilatación. En los ejemplos, demostrarás que existe una transformación de similitud entre dos círculos cualesquiera y por lo tanto, todos los círculos son similares.
Recordemos dos fórmulas importantes relacionadas con los círculos:
- Circunferencia (Perímetro) de un Círculo:\(C=2\pi r\)
- Área de un círculo:\(A=\pi r^{2}\)
Una vez que hayas demostrado que todos los círculos son similares, explorarás cómo se relacionan las circunferencias y áreas de círculos.
Demostrar similitud de círculo
- Considere el círculo\(A\), centrado en el punto\(A\) con radio\(r_A\), y el círculo\(D\), centrado en el punto\(D\) con radio\(rD\). Realizar una transformación rígida para llevar punto\(A\) a punto\(D\).
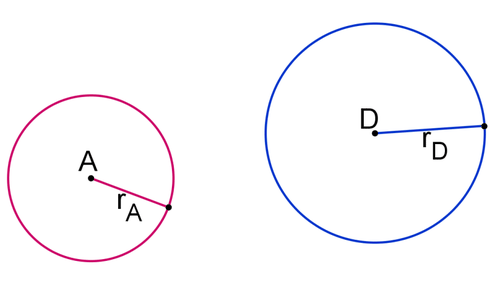
Dibuja un vector de punto\(A\) a punto\(D\). Traducir Circle\(A\)\) a lo largo del vector para crear círculo\(A′\). Tenga en cuenta que\(r_A \cong r′_A\).
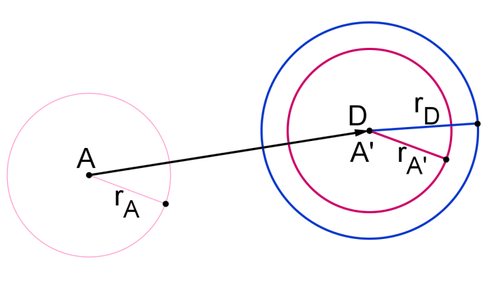
- Dilatar círculo\(A\) para mapearlo a círculo\(D\). ¿Puedes estar seguro de que los círculos son similares?
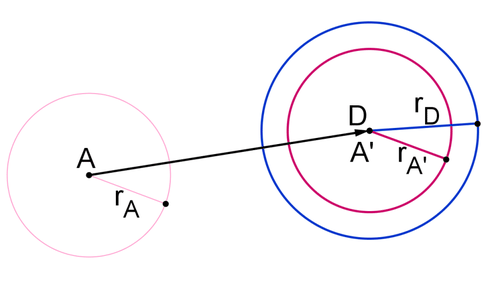
Debido a que el tamaño de un círculo está completamente determinado por su radio, puede usar los radios para encontrar el factor de escala correcto. Dilatar círculo\(A′\) alrededor del punto\(A′\) por un factor de escala de\(\dfrac{r_D}{r_{A′}}\).
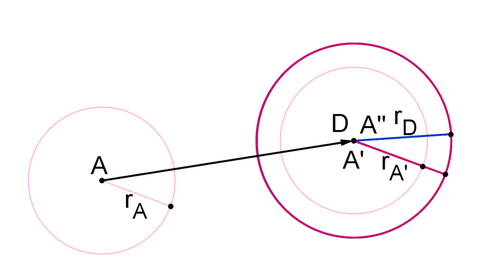
El círculo\(A′′\) es el mismo círculo\(A\) del círculo\(D\). Puedes estar seguro de esto porque\(r_{A′′}=\dfrac{r_D}{r_{A′}} \cdot r_{A′}=r_{D}\) y el punto\(A′′\) es lo mismo que punto\(D\). Debido a que un círculo se define por su centro y radio, si dos círculos tienen el mismo centro y radio entonces son el mismo círculo.
Esto significa que el círculo\(A\) es similar al círculo\(D\), porque una transformación de similitud (traducción luego dilatación) mapeó círculo\(A\) a círculo D\).
Círculo\(A\) y círculo\(D\) fueron dos círculos aleatorios. Esto demuestra que en general, todos los círculos son similares.
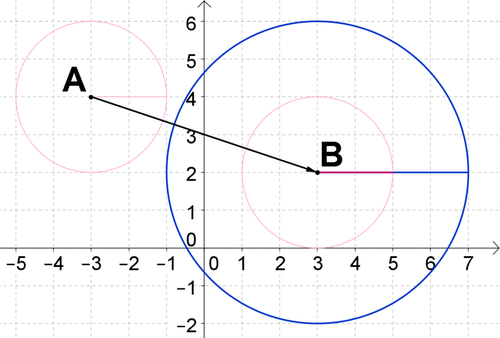
3. Mostrar que el círculo\(A\) con centro\((−3, 4)\) y radio 2 es similar al círculo\(B\) con centro\((3, 2)\) y radio 4.
Traducir círculo\(A\) a lo largo del vector de\((−3, 4)\) a\((3, 2)\). Después, dilatar la imagen alrededor de su centro en un factor de escala de 2. Habrás mapeado círculo\(A\) a círculo\(B\) con una transformación de similitud. Esto significa que el círculo\(A\) es similar al círculo\(B\).
Ejemplo\(\PageIndex{1}\)
Antes, te dieron un problema sobre Sean y sus dos círculos.
Sean tiene dos círculos, uno con un radio de 1 pulgada y otro con un radio de 3 pulgadas.
- ¿Cuál es la relación entre los radios de los círculos?
- ¿Cuál es el factor de escala entre los dos círculos?
- ¿Cuál es la relación entre las circunferencias de los círculos?
- ¿Cuál es la relación entre el área de los círculos?
- ¿Qué tienen que ver las relaciones de área y las proporciones de circunferencia con el factor de escala?
Solución
- La relación entre los radios es de 31.
- Existe un factor de escala porque dos círculos cualesquiera son similares. Se pueden utilizar los radios para determinar el factor de escala. La relación entre los radios es\(\dfrac{3}{1}\) así que el factor de escala es\(\dfrac{3}{1}=3\).
- La circunferencia del círculo más pequeño es\(C=2\pi (1)=2\pi\). La circunferencia del círculo más grande es\(C=2\pi (3)=6\pi\). La relación entre las circunferencias es\(\dfrac{6\pi}{2\pi}=\dfrac{3}{1}\).
- El área del círculo más pequeño es\(A=\pi (1)2=\pi\). El área del círculo más grande es\(A=\pi(3)^2=9\pi \). La relación entre las áreas es\(\dfrac{9\pi}{\pi}=\dfrac{9}{1}\). Tenga en cuenta que\(\dfrac{9}{1}=(\dfrac{3}{1})^2\).
- La relación de área es el factor de escala al cuadrado, porque el área es una medida bidimensional. La relación de circunferencia es igual al factor de escala, ya que la circunferencia es una medida unidimensional.
Ejemplo\(\PageIndex{2}\)
Mostrar que Círculo\(A\) con centro\((−1,7)\) y radio 2 es similar a Círculo\(B\) con centro\((4,6)\) y radio 3.
Solución
Traducir Círculo\(A\) a lo largo del vector de\((−1,7)\) a\((4,6)\). Después, dilatar la imagen alrededor de su centro con un factor de escala de\(\dfrac{3}{2}\). Habrás mapeado Círculo\(A\) a Círculo\(B\) con una transformación de similitud. Esto significa que Circle\(A\) es similar a Circle\(B\).
Ejemplo\(\PageIndex{3}\)
La relación entre la circunferencia del círculo\(D\) y la circunferencia del círculo\(C\) es\(\dfrac{4}{3}\). ¿Cuál es la proporción de sus áreas?
Solución
La relación de las circunferencias es la misma que el factor de escala. Por lo tanto, el factor de escala es\(\dfrac{4}{3}\). La relación de las áreas es el factor de escala al cuadrado. Por lo tanto, la proporción de las áreas es\((\dfrac{4}{3})^2=\dfrac{16}{9}\).
Ejemplo\(\PageIndex{4}\)
La relación entre el área del círculo\(F\) y el área del círculo\(E\) es\(\dfrac{9}{4}\). ¿Cuál es la proporción de sus radios?
Solución
La relación de las áreas es el factor de escala al cuadrado. Por lo tanto, el factor de escala es\(\sqrt{\dfrac{9}{4}}=\dfrac{3}{2}\). La relación de los radios es la misma que la del factor de escala, por lo que la relación de los radios es\(\dfrac{3}{2}\).
Revisar
Para #1 - #10, mostrar que los círculos son similares al describir la transformación de similitud necesaria para mapear un círculo sobre el otro.
- Círculo\(A\) con centro (2,7)\) y radio 4. Círculo\(B\) con centro\((1,−4)\) y radio 3.
- Círculo\(A\) con centro (6,4)\) y radio 3. Círculo\(B\) con centro\((−5,6)\) y radio 5.
- Círculo\(A\) con centro (1,4)\) y radio 2. Círculo\(B\) con centro\((3,−2)\) y radio 7.
- Círculo\(A\) con centro (8,1)\) y radio 6. Círculo\(B\) con centro\((6,−4)\) y radio 8.
- Círculo\(A\) con centro (−2,10)\) y radio 3. Círculo\(B\) con centro\((−1,−4)\) y radio 6.
- Círculo\(A\) con centro (−1,5) y radio 4. Círculo\(B\) con centro\((−1,5)\) y radio 5.
- Círculo\(A\) con centro (−4, −2) y radio 1. Círculo\(B\) con centro\((1,8)\) y radio 4.
- Círculo\(A\) con centro (10,3) y radio 5. Círculo\(B\) con centro\((4,2)\) y radio 8.
- Círculo\(A\) con centro (12,4) y radio 10. Círculo\(B\) con centro\((12,4)\) y radio 12.
- Círculo\(A\) con centro (−7,6) y radio 9. Círculo\(B\) con centro\((1,−4)\) y radio 9.
- La relación de la circunferencia de Círculo\(A\) a la circunferencia de Círculo\(B\) es\(\dfrac{2}{3}\). ¿Cuál es la proporción de sus radios?
- La relación entre el área de Círculo\(A\) y el área de Círculo\(B\) es\(\dfrac{6}{1}\). ¿Cuál es la proporción de sus radios?
- La relación entre el radio de Círculo\(A\) y el radio de Círculo\(B\) es\(\dfrac{5}{9}\). ¿Cuál es la proporción de sus áreas?
- La relación entre el área de Círculo\(A\) y el área de Círculo\(B\) es\(\dfrac{12}{5}\). ¿Cuál es la proporción de sus circunferencias?
- Para demostrar que dos círculos cualesquiera son similares es necesario realizar una traducción y/o una dilatación. ¿Por qué nunca necesitarás usar reflejos o rotaciones?
Reseña (Respuestas)
Para ver las respuestas de Revisar, abra este archivo PDF y busque la sección 8.1.
El vocabulario
| Término | Definición |
|---|---|
| Círculo | Un círculo es el conjunto de todos los puntos a una distancia específica de un punto dado en dos dimensiones. |
| Dilatación | Reducir o agrandar una figura según un factor de escala es una dilatación. |
| Radio | El radio de un círculo es la distancia desde el centro del círculo hasta el borde del círculo. |
| Transformación Rígida | Una transformación rígida es una transformación que conserva la distancia y los ángulos, no cambia el tamaño ni la forma de la figura. |
| Transformación de similitud | Una transformación de similitud es una o más transformaciones rígidas seguidas de una dilatación. |
Recursos adicionales
Elemento interactivo

