8.7: Software de Geometría para Traducciones
- Page ID
- 107634
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\(\newcommand{\longvect}{\overrightarrow}\)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Realizar y analizar traducciones usando Geogebra.
El software de geometría tiene una función de traducción que facilita la traducción de un objeto a lo largo de un vector. ¿Se puede realizar una traducción usando software de geometría sin esa función?
Traducciones
Recordemos que una traducción es un ejemplo de una transformación rígida. Una traslación mueve cada punto de una forma una distancia especificada en una dirección especificada definida por un vector. Abajo, el paralelogramo se ha traducido a lo largo del vector\ rightarrow {v}\) para crear un nuevo paralelogramo (la imagen).
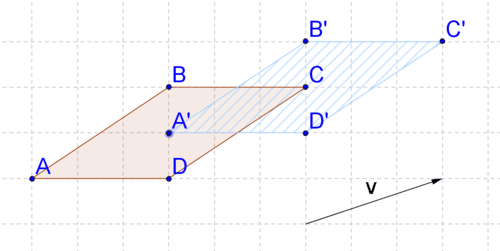
Cuando se trabaja en una cuadrícula (o papel cuadriculado), realizar traducciones es relativamente fácil. En la traducción anterior, se puede ver que el vector mueve cada punto una unidad hacia arriba y tres unidades hacia la derecha. Para realizar la traslación, basta con mover cada punto que defina el paralelogramo una unidad hacia arriba y tres unidades hacia la derecha. Pero, ¿y si la grilla no está ahí? Entonces, no es tan fácil describir la traducción porque no hay líneas de cuadrícula como guía.
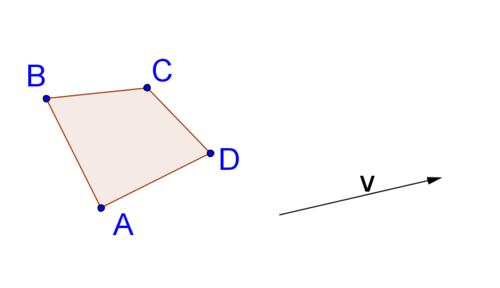
Para realizar una traducción sin cuadrícula, es necesario:
- Encuentra líneas paralelas al vector a través de cada uno de los puntos que definen la forma.
- Mueva la longitud del vector a lo largo de cada una de esas líneas.
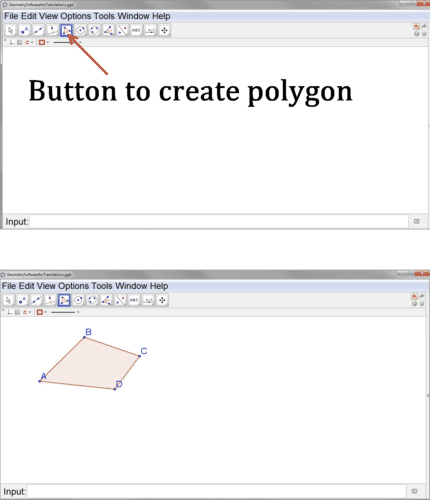
Hacer esto a mano requiere una cuidadosa construcción de líneas paralelas y copia de segmentos de línea. El software de geometría simplifica este proceso, porque el software de geometría tiene un botón de “traducir”. Geogebra es un ejemplo de software de geometría que se puede descargar gratis. Para realizar una traducción en Geogebra, primero crea tu polígono.
A continuación, crea el vector que definirá tu traducción. A continuación, se ha creado un vector de punto\(G\) a punto\(H\).
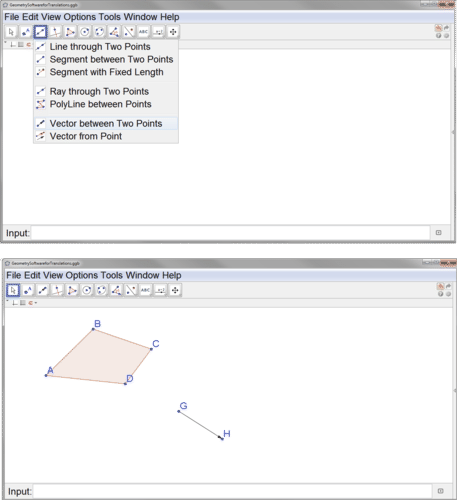
Para realizar la traducción, seleccione el botón de traducción, luego el polígono y luego el vector.
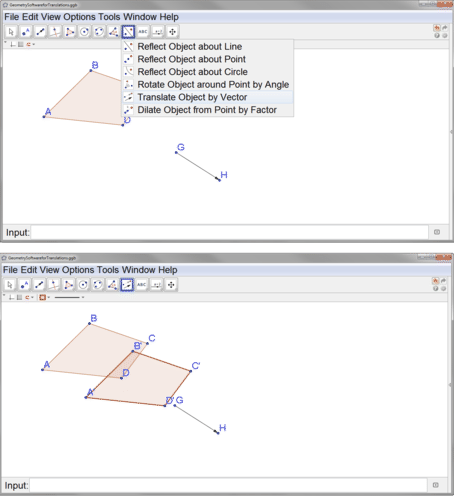
Tenga en cuenta que los puntos que definen la imagen están etiquetados con notación prima. Recuerde que la ubicación específica del vector no importa. En este punto puedes arrastrar el vector a otra ubicación y tu traducción no cambiará. También puedes mover puntos\(G\) o\(H\) redefinir el vector (o cambiar tu polígono original) y la ubicación de tu imagen se moverá en consecuencia.
Echemos un vistazo a un problema de ejemplo.
Mostrar que el segmento\(A\) con el que se conecta\(A′\) es paralelo al vector que conecta los puntos\(G\) y\(H\).
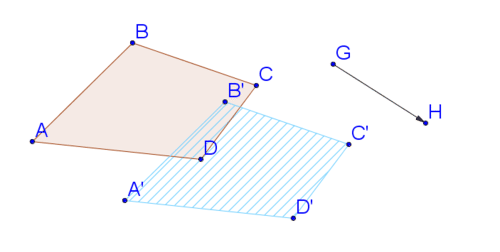
Utilice Geogebra para construir una línea paralela al vector a través del punto\(A\). Se puede ver que también pasa a través\(A′\). Esto significa que el segmento de línea\(A\) con el\(A′\) que se conecta es paralelo al vector.
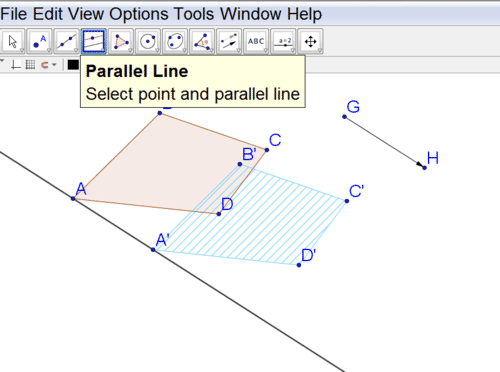
Traduce el polígono sin usar el botón de traducir.
Vas a utilizar Geogebra para hacer los mismos pasos que harías si estuvieras traduciendo a mano. Primero, construya líneas paralelas al vector a través de cada uno de los cuatro puntos que definen el cuadrilátero, utilizando el método del Ejemplo A.
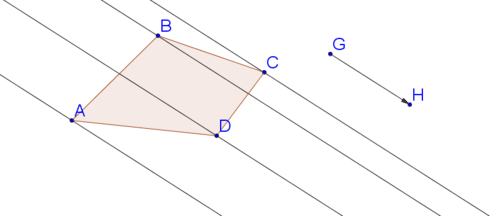
A continuación, copia el vector y pegarlo para que comience en el punto\(A\). Repita para puntos\(B\),\(C\), y\(D\). Tal vez tengas que asegurarte de que las copias de punto no\(H\) estén ocultas.
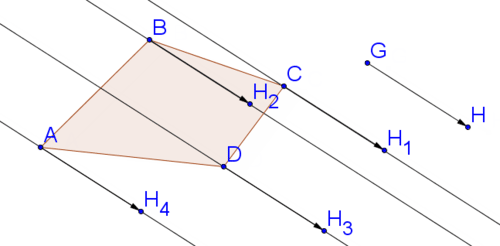
Formar un polígono con las copias de punto\(H\).
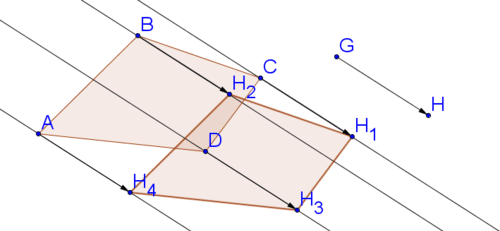
Ahora, comparemos y contrastemos los dos métodos para traducir un polígono usando Geogebra.
Usar el botón traducir es más rápido, pero realizar los pasos de construir las líneas paralelas y copiar los vectores también funciona y ayuda a mostrar la conexión entre líneas paralelas, vectores y traducciones. En ambos casos se puede mover el vector o la forma original después de que se haya realizado la traslación y la imagen cambiará y se moverá en consecuencia.
Ejemplo\(\PageIndex{1}\)
Anteriormente, se le preguntó si puede realizar una traducción utilizando software de geometría sin la función.
Solución
Puede realizar una traducción usando software de geometría sin el botón “traducir” construyendo líneas paralelas y copiando y pegando el vector en esas líneas.
Ejemplo\(\PageIndex{2}\)
Crea tu propio polígono y vector en Geogebra.
Ejemplo\(\PageIndex{3}\)
Traduzca el polígono a lo largo del vector usando el botón traducir.
Ejemplo\(\PageIndex{4}\)
Intenta traducir el polígono a lo largo del vector sin usar el botón traducir construyendo líneas paralelas y copiando y pegando el vector como se muestra en el Ejemplo B. ¿Cómo puedes verificar que lo has hecho correctamente?
Solución
Las respuestas variarán dependiendo del polígono que construyas. Mire hacia atrás en la sección de orientación para obtener ayuda con Geogebra. Para verificar que has realizado la traducción sin el botón de traducir correctamente, solo asegúrate de que ambas imágenes terminaron en el mismo lugar.
Revisar
- Crea un polígono en Geogebra.
- Crea un vector que moverá el polígono hacia la derecha.
- Traduce el polígono a lo largo del vector de #2 usando el botón traducir.
- Crea otro vector que moverá el polígono hacia arriba y hacia la izquierda.
- Traduce el polígono a lo largo del vector de #4 usando el botón traducir.
- Crea un tercer vector que moverá el polígono recto hacia abajo.
- Traduzca el polígono a lo largo del vector de #6 construyendo líneas paralelas y copiando y pegando el vector.
- Comprueba tu trabajo a #7 usando el botón traducir para traducir el polígono a lo largo del vector de #6. ¿Cómo se puede saber si realizó la traducción correctamente?
- Las traducciones son transformaciones rígidas, lo que significa que se conserva la distancia. Verifica que la distancia se haya conservado usando Geogebra para medir lados de tu polígono original y sus imágenes. Seleccione “distancia o longitud” de uno de los menús desplegables. Después, da clic en cada segmento de línea que desee medir para ver su longitud.
- Las traducciones son transformaciones rígidas, lo que significa que se conservan los ángulos. Verifique que los ángulos se hayan conservado usando Geogebra para medir dos ángulos correspondientes. Seleccione “ángulo” en el mismo menú desplegable que en #9. Entonces, dile a Geogebra qué ángulo quieres medir haciendo clic en los tres puntos que usarías para nombrar el ángulo. Debe hacer clic en los puntos en el sentido de las agujas del reloj para que mida el ángulo correcto.
- Construir un círculo en Geogebra.
- Crea un vector que moverá el círculo hacia la derecha.
- Traduce el círculo a lo largo del vector de #12 usando el botón traducir.
- Crea otro vector que moverá el círculo hacia arriba y hacia la izquierda.
- Traduce el círculo a lo largo del vector de #14 usando el botón traducir.
- Explora cómo podrías traducir el círculo sin usar el botón traducir creando líneas paralelas y copiando y pegando el vector.
Reseña (Respuestas)
Para ver las respuestas de Revisar, abra este archivo PDF y busque la sección 2.3.
El vocabulario
| Término | Definición |
|---|---|
| Traducción | Una traslación es una transformación que desliza una figura en el plano de coordenadas sin cambiar su forma, tamaño u orientación. |
| Transformación Rígida | Una transformación rígida es una transformación que conserva la distancia y los ángulos, no cambia el tamaño ni la forma de la figura. |

