8.9: Notación de traducción
- Page ID
- 107570
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Introducción gráfica a las traducciones de imágenes. Aprende a usar la notación para describir reglas de mapeo, y graficar imágenes dadas preimagen y traducción
Reglas para traducciones
Jack describe una traducción como un punto que se mueve de\(J(−2, 6)\) a\(J′(4,9)\). Escribe la regla de mapeo para describir esta traducción para Jack.
En geometría, una transformación es una operación que mueve, voltea o cambia una forma (llamada preimagen) para crear una nueva forma (llamada imagen). Una traslación es un tipo de transformación que mueve cada punto de una figura a la misma distancia en la misma dirección. Las traducciones a menudo se denominan diapositivas. Se puede describir una traducción usando palabras como “movido hacia arriba 3 y más de 5 a la izquierda” o con notación. Hay dos tipos de notación que hay que conocer.
- Parece una notación\(T_{(3, 5)}\). Esta notación le indica que agregue 3 a los\(x\) valores y agregue 5 a los\(y\) valores.
- La segunda notación es una regla de mapeo de la forma\((x,y) \rightarrow (x−7, y+5)\). Esta notación le dice que las\(y\) coordenadas\(x\) y se traducen a\(x−7\) y\(y+5\).
La notación de reglas de mapeo es la más común.
Elemento Interactivo
Escribamos una regla de mapeo para cada una de las siguientes traducciones:
- Sarah describe una traducción como un punto que\(P\) se mueve de\(P(−2,2)\) a\(P′(1,−1)\).
En general,\(P(x, y) \rightarrow P′(x+a, y+b)\).
En este caso,\(P(−2, 2) \rightarrow P′(−2+a, 2+b)\) o\(P(−2, 2) \rightarrow P′(1, −1)\)
Por lo tanto:
\ (\ begin {array} {rr}
-2+a=1 &\ text {y}\ quad 2+b=-1\
a=3 &\ quad b=-3
\ end {array}\)
La regla es:\((x,y) \rightarrow (x+3, y−3)\)
- Mikah describe una traducción como punto D en un diagrama que se mueve de\(D(1, −5)\) a\(D′(−3,1)\).
En general,\(P(x,y) \rightarrow P′(x+a, y+b)\).
En este caso,\(D(1,−5) \rightarrow D′(1+a,−5+b)\) o\(D(1,−5) \rightarrow D′(−3,1)\)
Por lo tanto:
\ (\ begin {array} {rrr}
1+a=-3 &\ text {y} & -5+b=1\\
a=-4 & & b=6
\ end {array}\)
La regla es:\((x,y) \rightarrow (x−4, y+6)\)
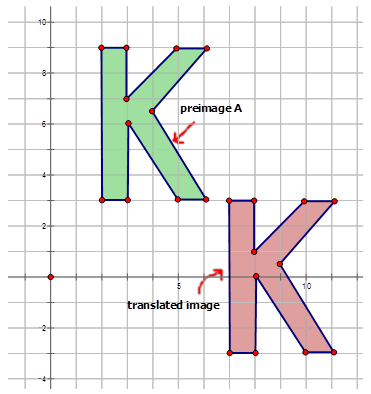
- La traducción de la preimagen\(A\) a la imagen traducida\(J\) en el siguiente diagrama:
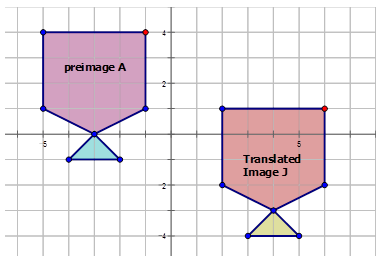
Primero, elige un punto en el diagrama para usar para ver cómo se traduce.
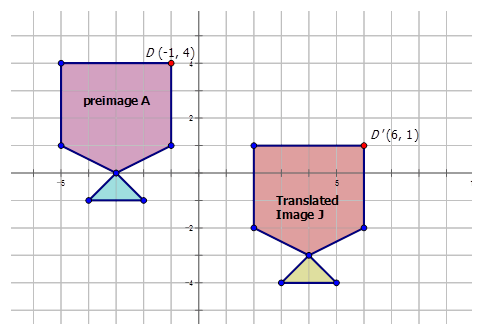
\(D:(−1,4) D′:(6,1)\)
\(D(x,y) \rightarrow D′(x+a,y+b)\)
Entonces:\(D(−1,4) \rightarrow D′(−1+a,4+b)\) o\(D(−1,4) \rightarrow D′(6,1)\)
Por lo tanto:
\ (\ begin {array} {rrr}
-1+a=6 &\ text {y} & 4+b=1\\
a=7 & & b=-3
\ end {array}\)
La regla es:\((x,y) \rightarrow (x+7,y−3)\)
Ejemplo\(\PageIndex{1}\)
Anteriormente, le dijeron que Jack describió una traducción como un punto que\(J\) se mueve de\(J(−2,6)\) a\(J′(4,9)\). ¿Cuál es la regla de mapeo que describe esta traducción?
Solución
\((x,y) \rightarrow (x+6, y+3)\)
Ejemplo\(\PageIndex{2}\)
Escribe la regla de mapeo que representa la traducción del triángulo rojo al triángulo verde traducido en el diagrama de abajo.
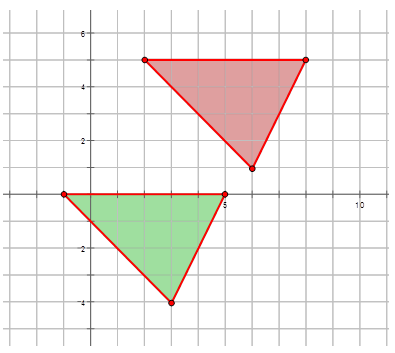
Solución
\((x, y) \rightarrow (x−3, y−5)\)
Ejemplo\(\PageIndex{3}\)
El siguiente patrón es parte del papel pintado que se encuentra en el lobby de un hotel. Escriba la regla de mapeo que representa la traducción de un trapecio azul a un trapecio azul traducido que se muestra en el diagrama a continuación.
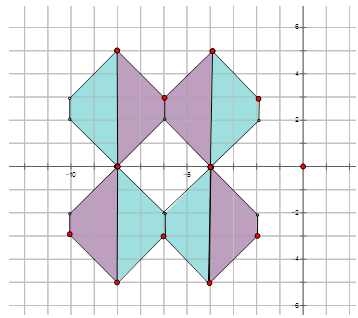
Solución
Si miras de cerca el diagrama a continuación, hay dos pares de trapecios que son traducciones entre sí. Por lo tanto puedes elegir un trapecio azul que sea una traslación del otro y escoger un punto para averiguar cuánto se ha movido la forma para llegar a la posición traducida.
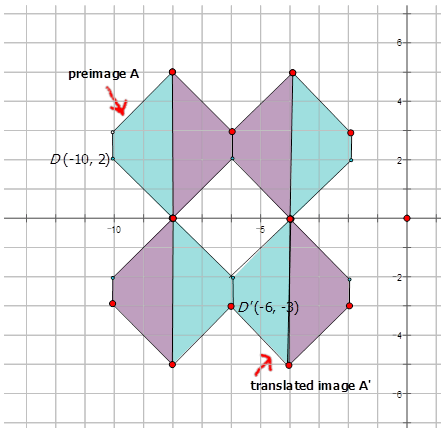
Para esos dos trapecios:\((x,y) \rightarrow (x+4, y−5)\)
Revisar
Escribe la regla de mapeo para describir el movimiento de los puntos en cada una de las traducciones a continuación.
- \(S(1,5) \rightarrow S′(2,7)\)
- \(W(−5,−1) \rightarrow W′(−3,1)\)
- \(Q(2,−5) \rightarrow Q′(−6,3)\)
- \(M(4,3) \rightarrow M′(−2,9)\)
- \(B(−4,−2) \rightarrow B′(2,−2)\)
- \(A(2,4) \rightarrow A′(2,6)\)
- \(C(−5,−3) \rightarrow C′(−3,4)\)
- \(D(4,−1) \rightarrow D′(−4,2)\)
- \(Z(7,2) \rightarrow Z′(−3,6)\)
- \(L(−3,−2) \rightarrow L′(4,−1)\)
Escribe la regla de mapeo que representa la traducción de la preimagen a la imagen para cada diagrama a continuación.
-
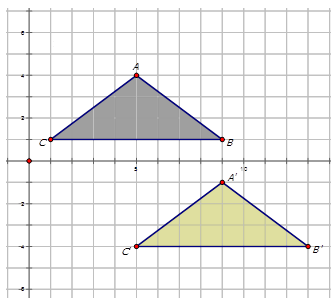
Figura\(\PageIndex{6}\) -
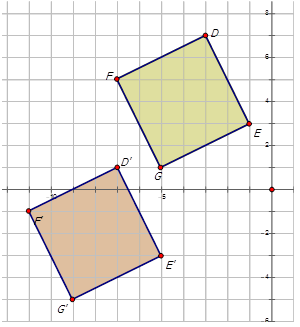
Figura\(\PageIndex{7}\) -
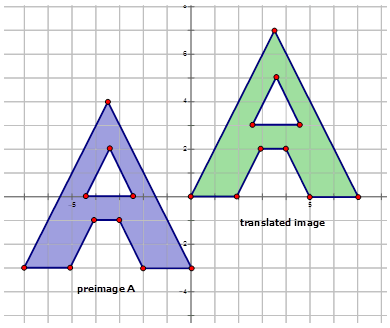
Figura\(\PageIndex{8}\) -
Figura\(\PageIndex{9}\) -
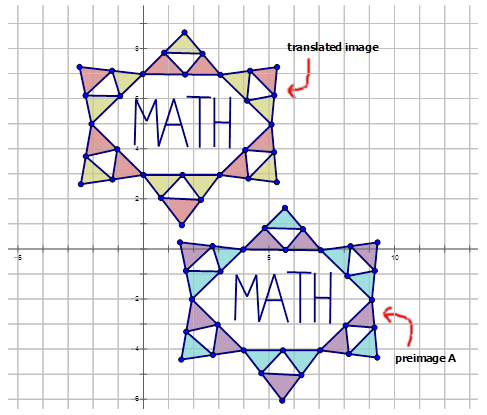
Figura\(\PageIndex{10}\)
Reseña (Respuestas)
Para ver las respuestas de Revisar, abra este archivo PDF y busque la sección 10.3.
Recursos adicionales
Elemento Interactivo
Video: Cuadrantes de plano de coordenadas
Práctica: Notación de traducción