8.12: Software de Geometría y Rotaciones Gráficas
- Page ID
- 107576
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\(\newcommand{\longvect}{\overrightarrow}\)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Grafica imágenes giradas dadas la preimagen y el número de grados. Realizar rotaciones usando Geogebra.
Cuadrilátero\(WXYZ\) tiene coordenadas\(W(−5,−5)\),\(X(−2,0), \(Y(2,3)\) y\(Z(−1,3)\). Dibuja el cuadrilátero en el plano cartesiano. Gire la imagen en\(110^{\circ}\) sentido antihorario sobre el punto\(X\). Mostrar la imagen resultante.
Gráficas de Rotaciones
En geometría, una transformación es una operación que mueve, voltea o cambia una forma para crear una nueva forma. Una rotación es un ejemplo de una transformación donde una figura se gira alrededor de un punto específico (llamado centro de rotación), un cierto número de grados.
Por ahora, para poder graficar una rotación en general utilizarás software de geometría. Esto te permitirá rotar cualquier figura cualquier número de grados alrededor de cualquier punto. Hay algunas rotaciones comunes que son buenas para saber cómo prescindir del software de geometría, que se muestran en la tabla a continuación.
| Centro de Rotación | Ángulo de rotación | Preimagen (Punto\(P\)) | Imagen girada (punto\(P′\)) |
|---|---|---|---|
| \((0, 0)\) | \(90^{\circ}\)(o\ (−270^ {\ circ}) | \ (P\))” class="lt-k12-6056">\((x,y)\) | \ (P′\))” class="lt-k12-6056">\((−y,x)\) |
| \((0, 0)\) | \(180^{\circ}\)(o\(−180^{\circ}\)) | \ (P\))” class="lt-k12-6056">\((x,y)\) | \ (P′\))” class="lt-k12-6056">\((−x,−y)\) |
| \((0, 0)\) | \(270^{\circ}\)(o\(−90^{\circ}\)) | \ (P\))” class="lt-k12-6056">\((x,y)\) | \ (P′\))” class="lt-k12-6056">\((y,−x)\) |
Dibujemos la preimagen y la imagen y etiquetemos adecuadamente cada una para la siguiente transformación:
La línea\(\overline{AB}\) trazada de\((-4, 2)\) a se\((3, 2)\) ha girado alrededor del origen en un ángulo de\(90^{\circ}\) CW.
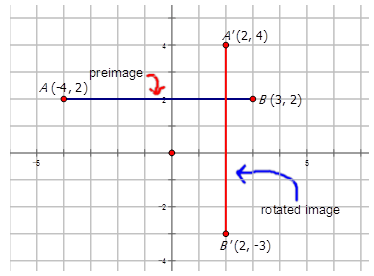
Ahora, dibujemos y etiquetemos la imagen girada para las siguientes rotaciones:
- El diamante\(ABCD\) se gira\(145^{\circ}\) CCW alrededor del origen para formar la imagen\(A′B′C′D′\).
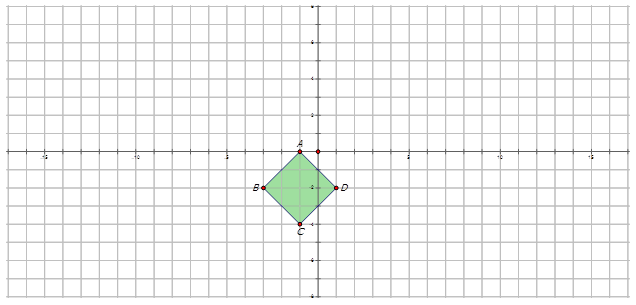
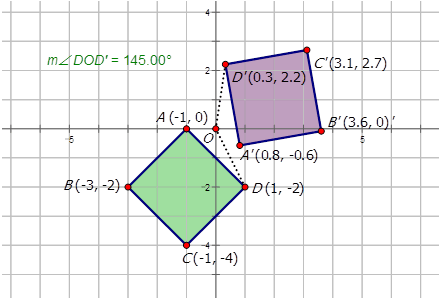
Observe que la dirección es en sentido antihorario.
- La siguiente figura se gira alrededor del origen\(200^{\circ}\) CW para hacer una imagen rotada.
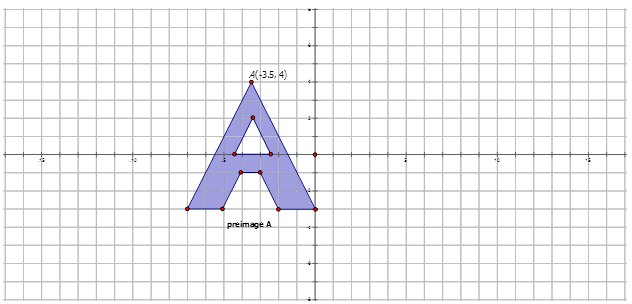
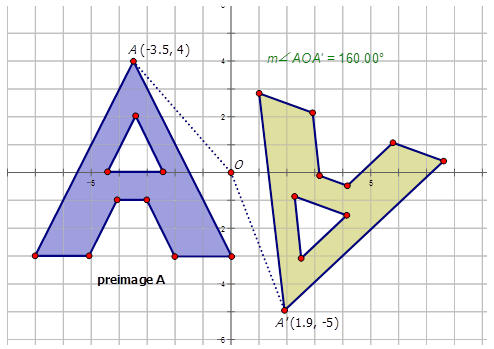
Observe que la dirección de la rotación es en sentido antihorario, por lo tanto el ángulo de rotación es\(160^{\circ}\).
Ejemplo\(\PageIndex{1}\)
Antes, te preguntaron sobre el cuadrilátero\(WXYZ\) tiene coordenadas\(W(−5,−5)\),\(X(−2,0)\), Y (2,3)\) y\(Z(−1,3)\). Dibuja el cuadrilátero en el plano cartesiano. Gire la imagen\(110^{\circ}\) en sentido antihorario sobre el punto X\). Mostrar la imagen resultante.
Solución
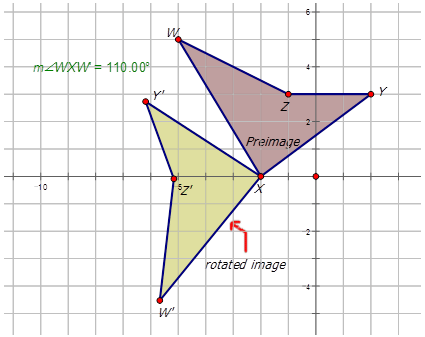
Ejemplo\(\PageIndex{2}\)
La línea\(\overline{ST}\) dibujada de\((-3, 4)\) a se\((-3, 8)\) ha girado\(60^{\circ}\) CW alrededor del punto\(S\). Dibuja la preimagen y la imagen y etiquete adecuadamente cada una.
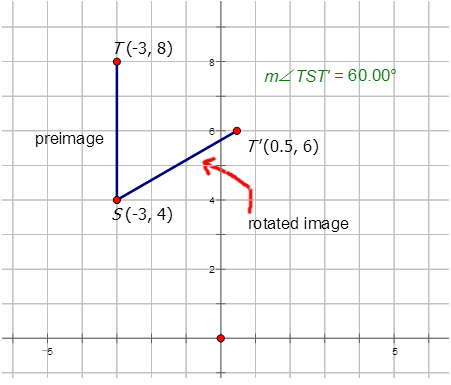
Solución
Observe que la dirección del ángulo es en sentido horario, por lo tanto la medida del ángulo es\(60^{\circ}\) CW o\(−60^{\circ}\).
Ejemplo\(\PageIndex{3}\)
El polígono de abajo se ha girado\(155^{\circ}\) CCW sobre el origen. Dibuja la imagen girada y etiquete adecuadamente cada una.
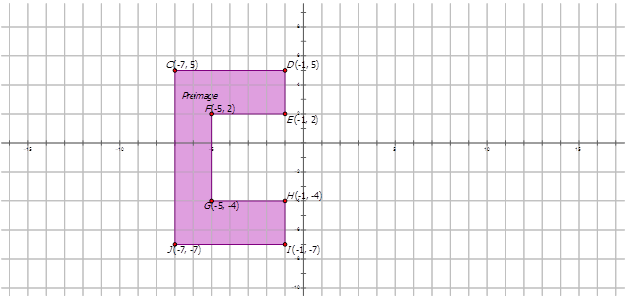
Solución
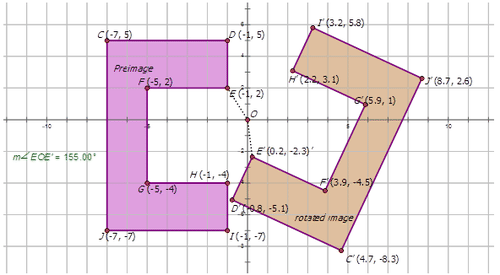
Observe que la dirección del ángulo es en sentido antihorario, por lo tanto, la medida del ángulo es\(155^{\circ}\) CCW o\(155^{\circ}\).
Ejemplo\(\PageIndex{4}\)
El pentágono púrpura se gira alrededor del punto\(225^{\circ}\) A. Encuentra las coordenadas del pentágono púrpura. En el diagrama, dibuje y etiquete el pentágono girado.
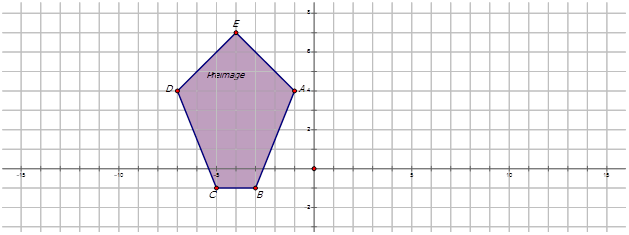
Solución
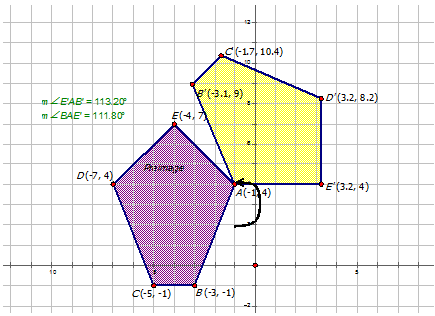
La medida de\(\angle BAB′=m\angle BAE′+m\angle E′AB′\). Por lo tanto\(\angle BAB′=111.80^{\circ} +113.20^{\circ}\) o\(225^{\circ}\). Observe que la dirección del ángulo es en sentido antihorario, por lo tanto, la medida del ángulo es\(225^{\circ}\) CCW o\(225^{\circ}\).
Revisar
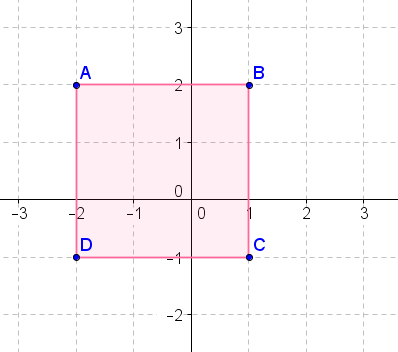
- Gire la figura anterior\(90^{\circ}\) en sentido horario sobre el origen.
- Gire la figura anterior\(270^{\circ}\) en sentido horario sobre el origen.
- Gire la figura anterior\(180^{\circ}\) sobre el origen.
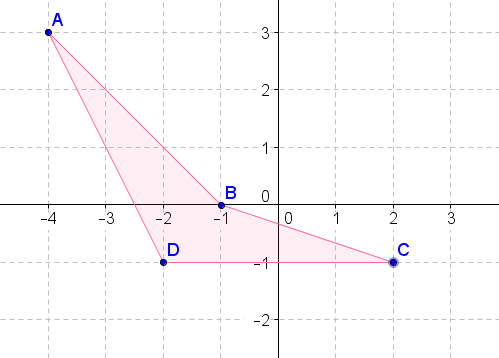
- Gire la figura anterior en\(90^{\circ}\) sentido antihorario sobre el origen.
- Gire la figura anterior en\(270^{\circ}\) sentido antihorario sobre el origen.
- Gire la figura anterior\(180^{\circ}\) sobre el origen.
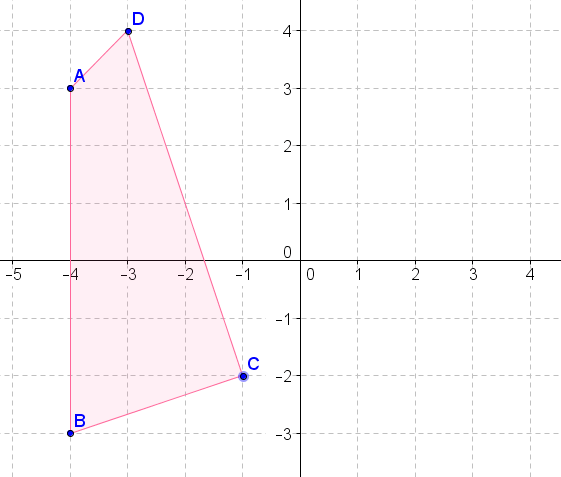
- Gire la figura anterior\(90^{\circ}\) en sentido horario sobre el origen.
- Gire la figura anterior\(270^{\circ}\) en sentido horario sobre el origen.
- Gire la figura anterior\(180^{\circ}\) sobre el origen.
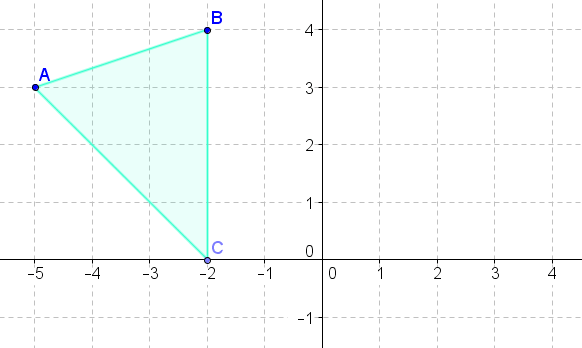
- Gire la figura anterior en\(90^{\circ}\) sentido antihorario sobre el origen.
- Gire la figura anterior en\(270^{\circ}\) sentido antihorario sobre el origen.
- Gire la figura anterior\(180^{\circ}\) sobre el origen.
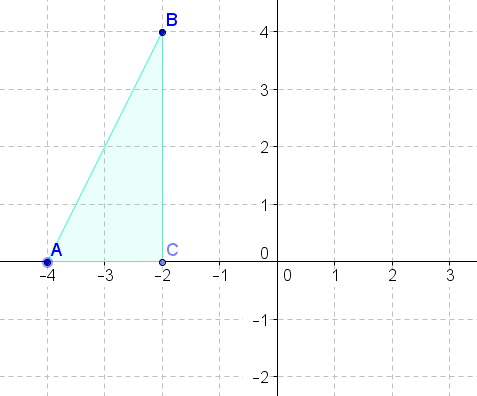
- Gire la figura anterior\(90^{\circ}\) en sentido horario sobre el origen.
- Gire la figura anterior\(270^{\circ}\) en sentido horario sobre el origen.
- Gire la figura anterior\(180^{\circ}\) sobre el origen.
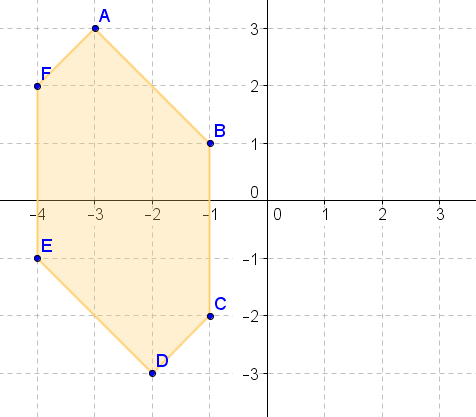
- Gire la figura anterior en\(90^{\circ}\) sentido antihorario sobre el origen.
- Gire la figura anterior en\(270^{\circ}\) sentido antihorario sobre el origen.
- Gire la figura anterior\(180^{\circ}\) sobre el origen.
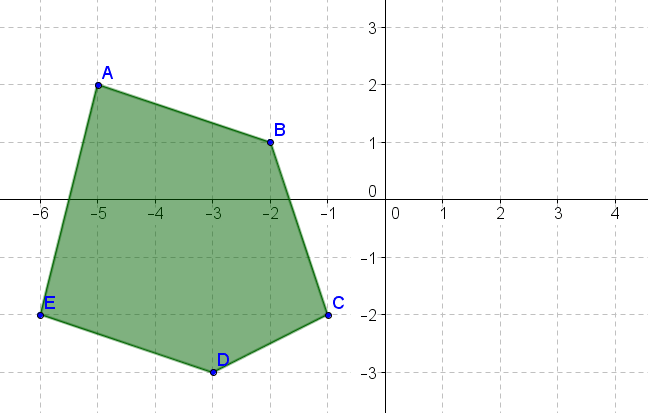
- Gire la figura anterior\(90^{\circ}\) en sentido horario sobre el origen.
- Gire la figura anterior\(270^{\circ}\) en sentido horario sobre el origen.
- Gire la figura anterior\(180^{\circ}\) sobre el origen.
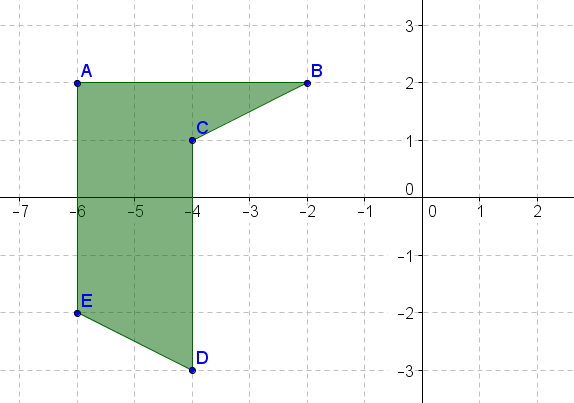
- Gire la figura anterior en\(90^{\circ}\) sentido antihorario sobre el origen.
- Gire la figura anterior en\(270^{\circ}\) sentido antihorario sobre el origen.
- Gire la figura anterior\(180^{\circ}\) sobre el origen.
Reseña (Respuestas)
Para ver las respuestas de Revisar, abra este archivo PDF y busque la sección 10.8.
El vocabulario
| Término | Definición |
|---|---|
| Rotación | Una rotación es una transformación que convierte una figura en el plano de coordenadas un cierto número de grados alrededor de un punto dado sin cambiar la forma o el tamaño de la figura. |
Recursos adicionales
Práctica: Software de Geometría y Rotaciones Gráficas

