8.13: Definir la reflexión
- Page ID
- 107573
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\(\newcommand{\longvect}{\overrightarrow}\)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Transformaciones que convierten una figura en su imagen especular volteándola sobre una línea.
Reflexiones
Una transformación es una operación que mueve, voltea o cambia de otra manera una figura para crear una nueva figura. Una transformación rígida (también conocida como transformación de isometría o congruencia) es una transformación que no cambia el tamaño o la forma de una figura.
Las transformaciones rígidas son traslaciones, reflexiones y rotaciones. La nueva figura creada por una transformación se llama la imagen. La figura original se llama la preimagen. Si la preimagen es A, entonces la imagen sería\(A′\), dijo “un primo”. Si hay una imagen de\(A′\), eso sería etiquetado\(A′′\), dijo “un doble primo”.
Un reflejo es una transformación que convierte una figura en su imagen especular volteándola sobre una línea. La línea de reflexión es la línea sobre la que se refleja una figura. Si un punto está en la línea de reflexión entonces la imagen es la misma que la preimagen. Las imágenes son siempre congruentes con las preimágenes.

Si bien puedes reflexionar sobre cualquier línea, algunas líneas comunes de reflexión tienen reglas que vale la pena memorizar:
Reflexión sobre el\(y\) eje:\((x,y)\rightarrow (−x,y)\)
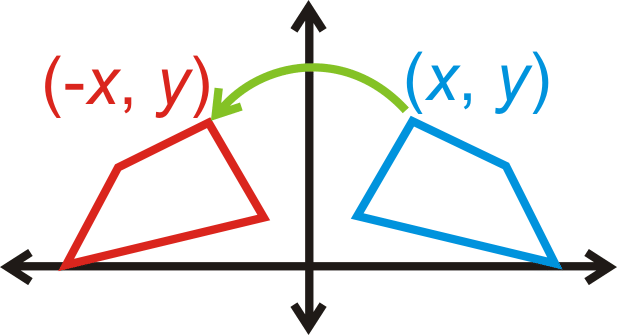
Reflexión sobre el\(x\) eje:\((x,y)\rightarrow (x,−y)\)
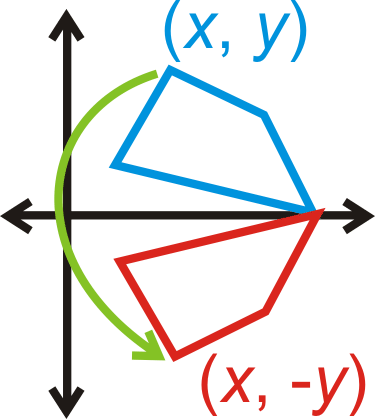
Reflexión sobre\(y=x\):\((x,y)\rightarrow (y,x)\)
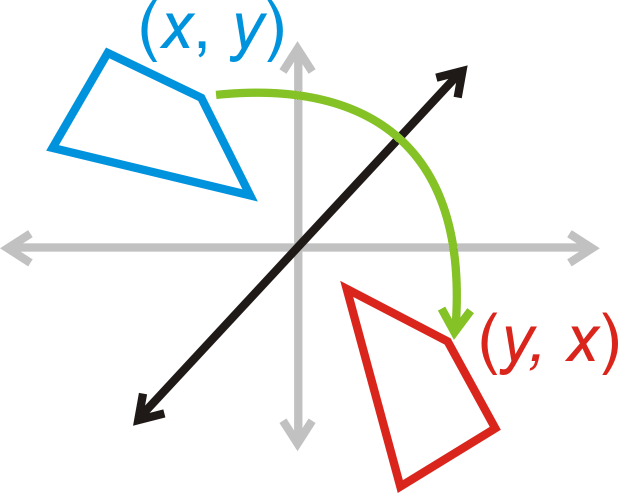
Reflexión sobre\(y=−x\):\((x,y)\rightarrow (−y,−x)\)
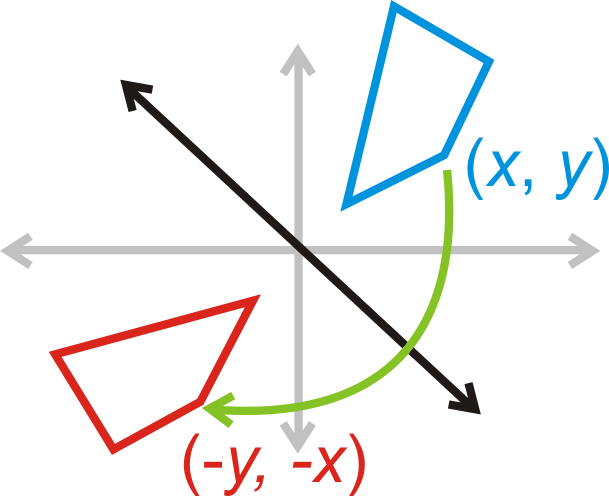
¿Y si te dieran las coordenadas de un cuadrilátero y se te pidiera reflejar ese cuadrilátero sobre el\(y\) eje? ¿Cuáles serían sus nuevas coordenadas?
Ejemplo\(\PageIndex{1}\)
Reflexionar\(\Delta ABC\) sobre el\(y\) eje. Encuentra las coordenadas de la imagen.
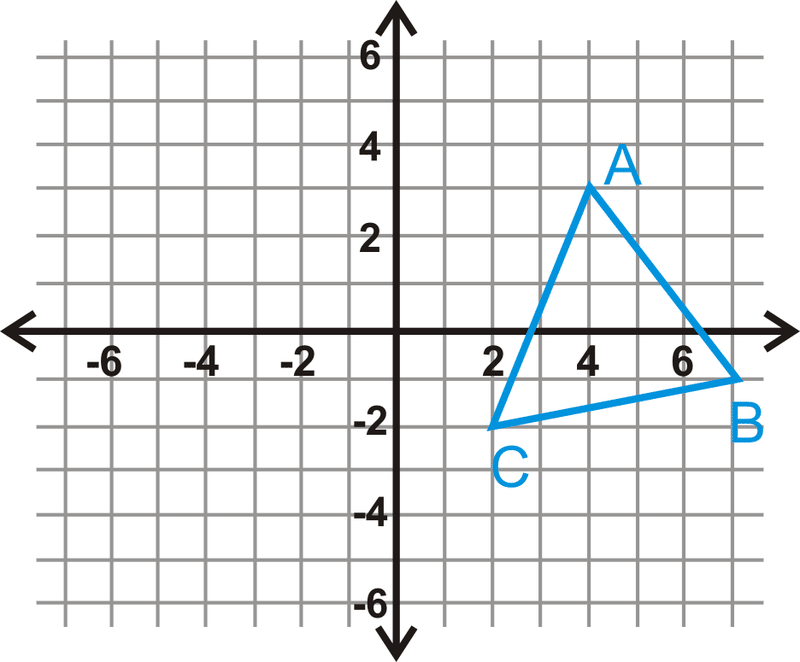
Solución
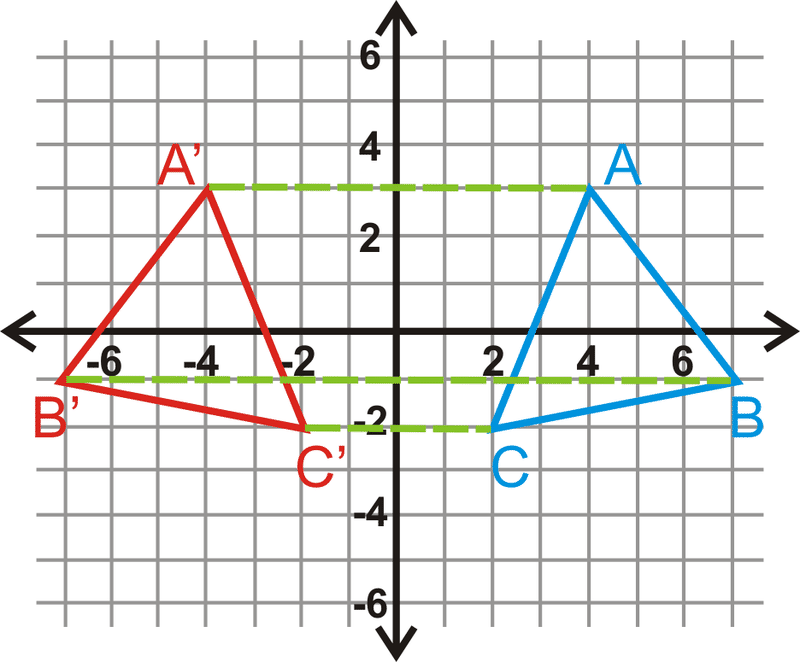
\(\Delta A′B′C′\)estará a la misma distancia del\(y\) eje -que\(\Delta ABC\), pero en el otro lado. De ahí que sus\(x\) coordenadas sean opuestas.
\(\begin{aligned} &A(4,3)\rightarrow A′(−4,3) \\ &B(7,−1)\rightarrow B′(−7,−1) \\ &C(2,−2)\rightarrow C′(−2,−2)\end{aligned}\)
Ejemplo\(\PageIndex{2}\)
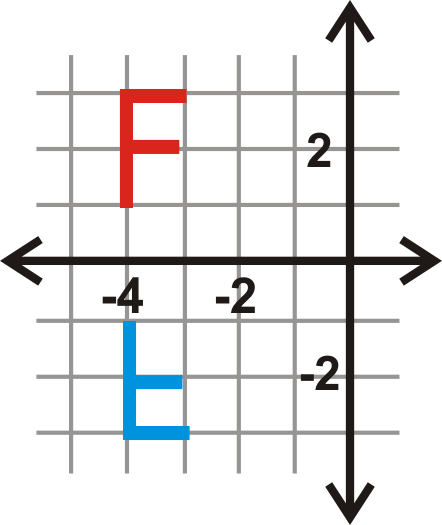
Refleja la letra “\(F\)′′ sobre el\(x\) eje.
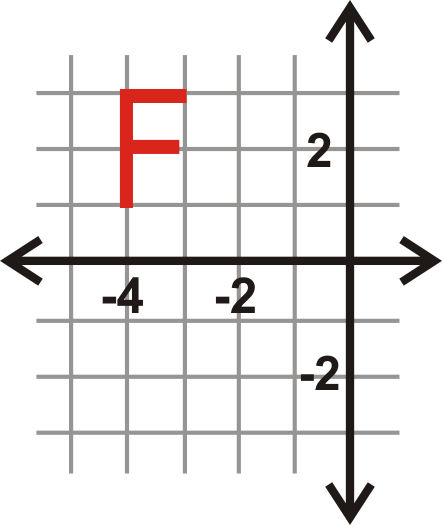
Solución
Al reflejar la letra F sobre el\(x\) eje -axis, las\(y\) coordenadas −estarán a la misma distancia del\(x\) eje -pero en el otro lado del\(x\) eje -axis. De ahí que sus\(y\) coordenadas sean opuestas.
Ejemplo\(\PageIndex{3}\)
Refleja el triángulo\(\Delta ABC\) con vértices\(A(4,5)\),\(B(7,1)\) y\(C(9,6)\) sobre la línea\(x=5\). Encuentra las coordenadas de\(A′\),\(B′\), y\(C′\).
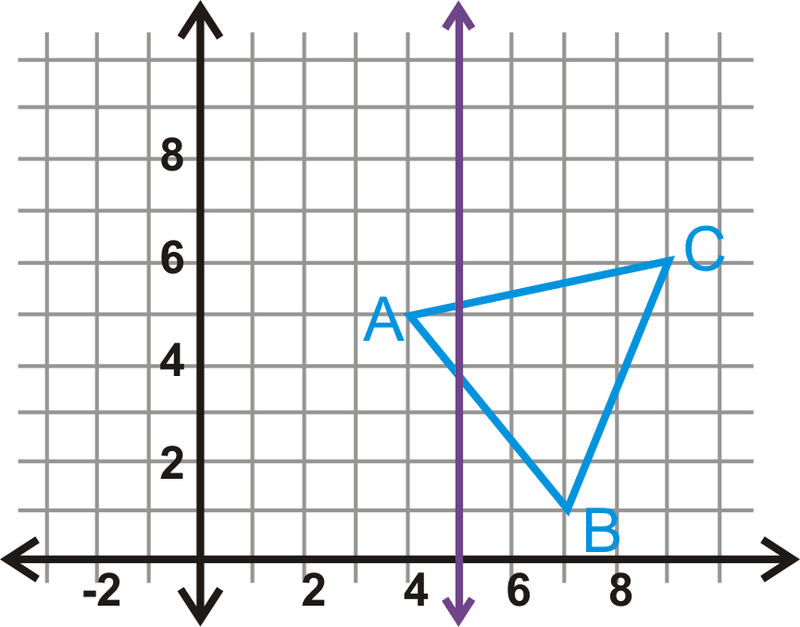
Solución
Los vértices de la imagen están a la\(x=5\) misma distancia que los de la preimagen.
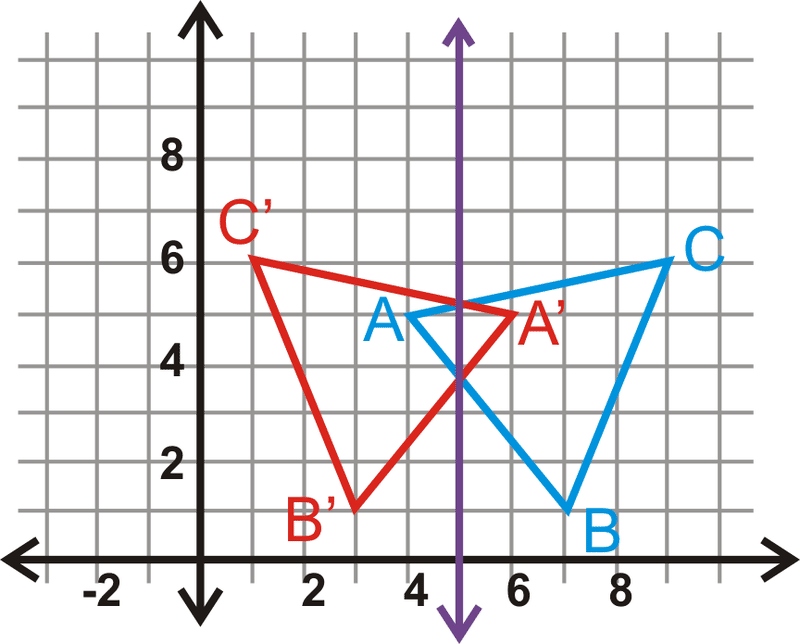
\(\begin{aligned} A(4,5)\rightarrow A′(6,5) \\ &B(7,1)\rightarrow B′(3,1) \\ &C(9,6)\rightarrow C′(1,6) \end{aligned}\)
Ejemplo\(\PageIndex{4}\)
Refleja el segmento de línea\(\overline{PQ}\) con puntos finales\(P(−1,5)\) y\(Q(7,8)\) sobre la línea\(y=5\).
Solución
P está en la línea de reflexión, lo que significa que\(P′\) tiene las mismas coordenadas. \(Q′\)está a la misma distancia de\ (y=5, pero del otro lado.
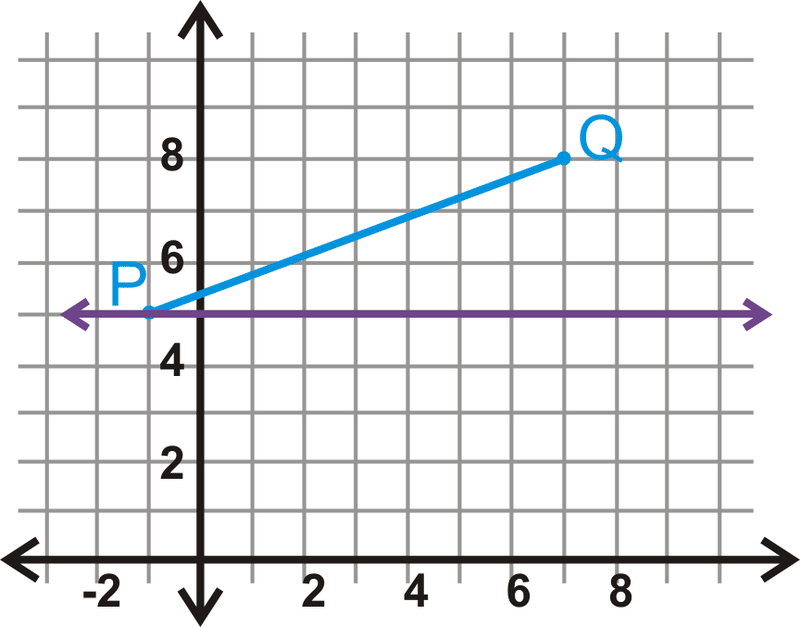
\(\begin{aligned}P(−1,5)&\rightarrow P′(−1,5) \\ Q(7,8)&\rightarrow Q′(7,2)\end{aligned}\)
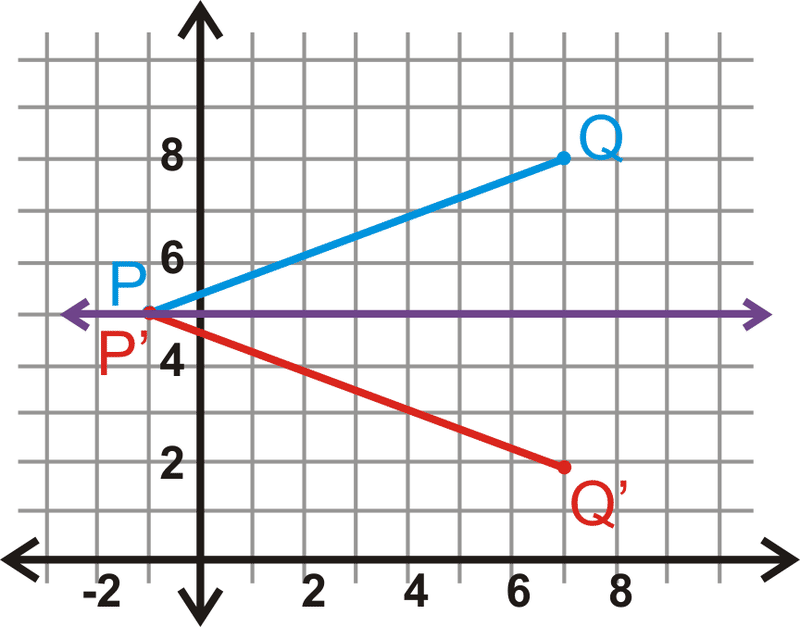
Ejemplo\(\PageIndex{5}\)
Un triángulo\(\Delta LMN\) y su reflejo,\(\Delta L′M′N′\) están abajo. ¿Cuál es la línea de reflexión?
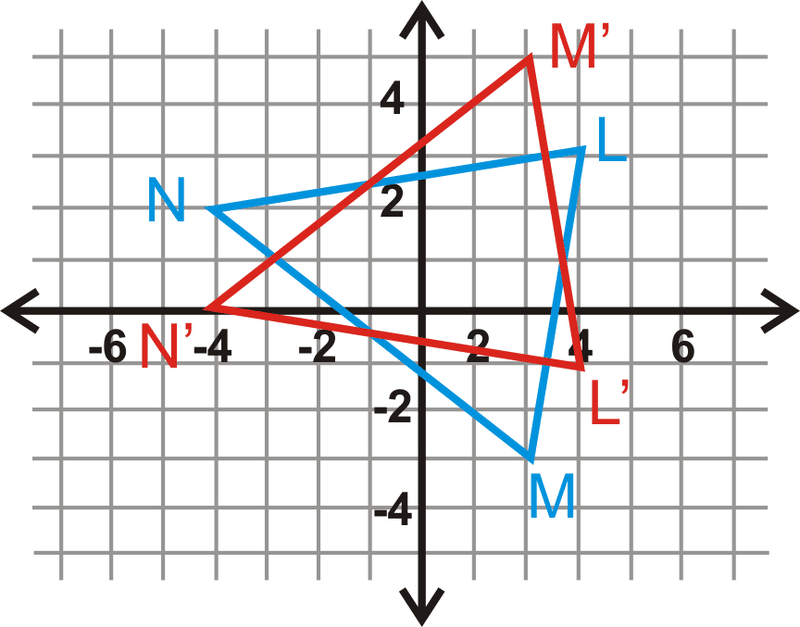
Solución
Al mirar la gráfica, vemos que las partes correspondientes de la preimagen y la imagen se cruzan cuando\(y=1\). Por lo tanto, esta es la línea de reflexión.
Si la imagen no se cruza con la preimagen, busque el punto medio entre el punto de preimagen y su imagen. Este punto está en la línea de reflexión.
Ejemplo\(\PageIndex{6}\)
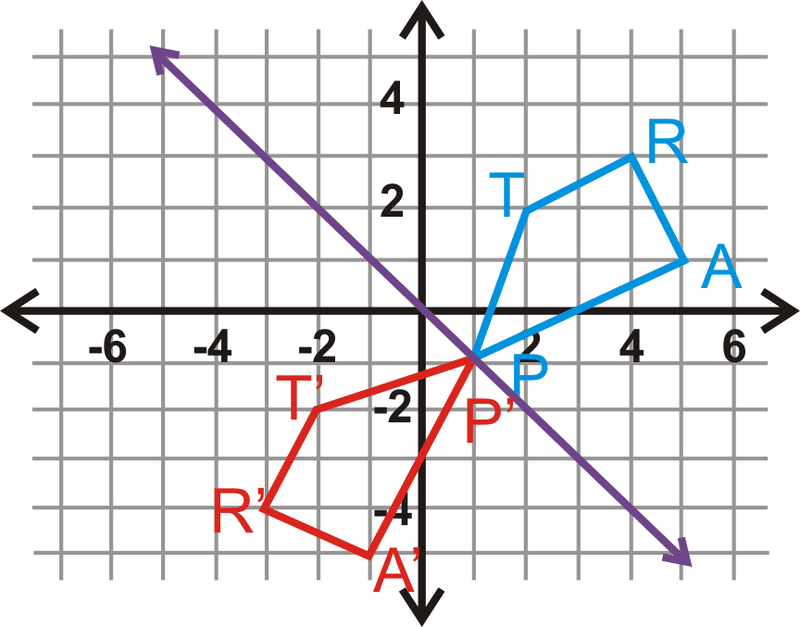
Refleja el trapecio\(TRAP\) sobre la línea\(y=−x\).
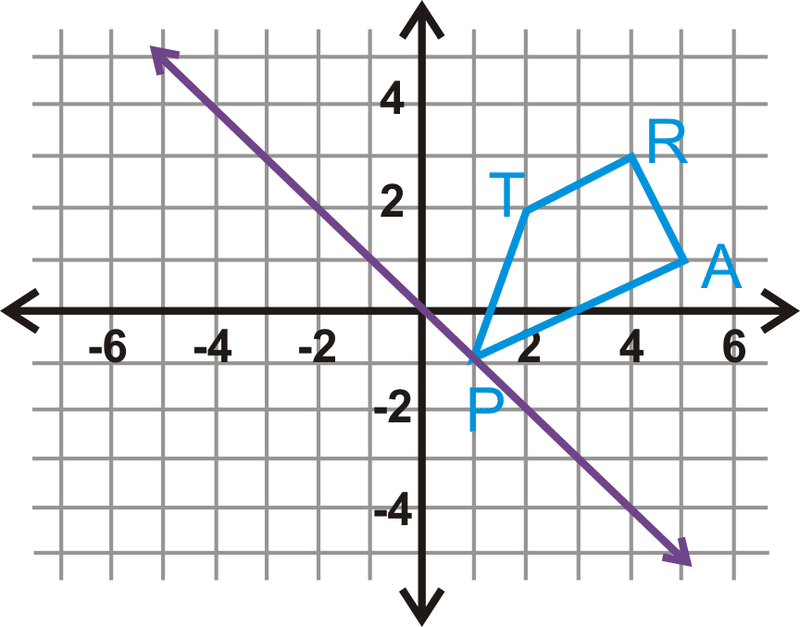
Solución
La línea púrpura es\(y=−x\). Se puede reflejar el trapecio sobre esta línea.
\(\begin{aligned} T(2,2)\rightarrow T′(−2,−2) \\ R(4,3)\rightarrow R′(−3,−4) \\ A(5,1)&\rightarrow A′(−1,−5) \\ P(1,−1)&\rightarrow P′(1,−1) \end{aligned}\)
Revisar
- Si\((5,3)\) se refleja sobre el\(y\) eje -eje, ¿cuál es la imagen?
- Si\((5,3)\) se refleja sobre el\(x\) eje -eje, ¿cuál es la imagen?
- Si\((5,3)\) se refleja sobre\(y=x\), ¿cuál es la imagen?
- Si\((5,3)\) se refleja sobre\(y=−x\), ¿cuál es la imagen?
- Trazar las cuatro imágenes. ¿Qué forma hacen? Ser específico.
- ¿Qué letra es un reflejo sobre una línea vertical de la letra “\(b\)′′”?
- ¿Qué letra es un reflejo sobre una línea horizontal de la letra “\(b\)′′”?
Refleja cada forma sobre la línea dada.
- \(y\)-eje
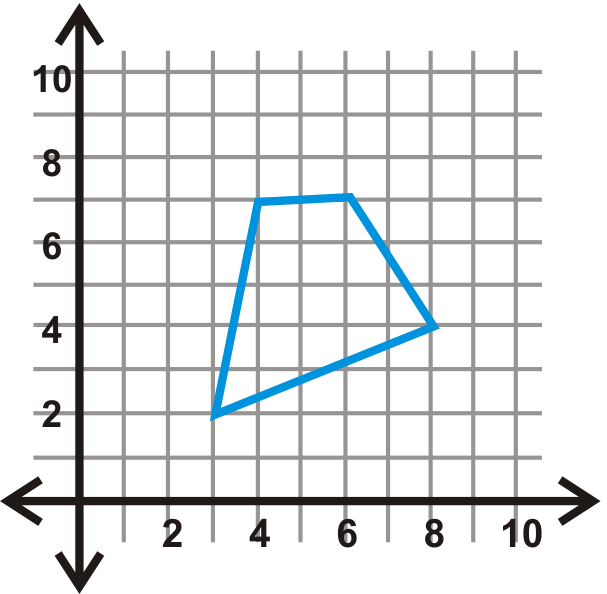
Figura\(\PageIndex{17}\) - \(x\)-eje
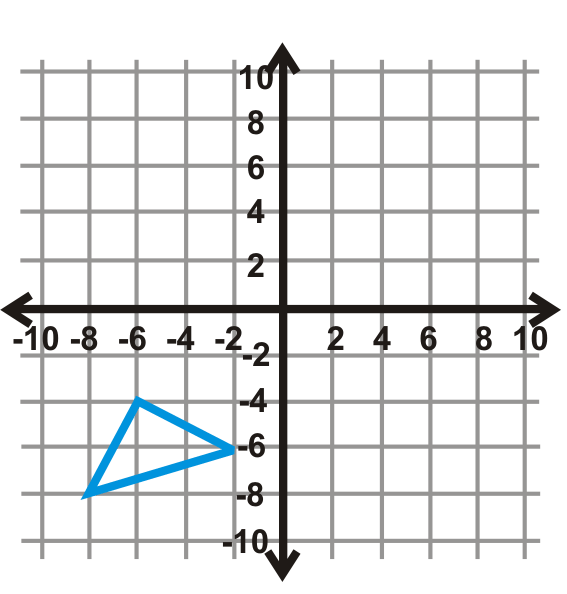
Figura\(\PageIndex{18}\) - \(y=3\)
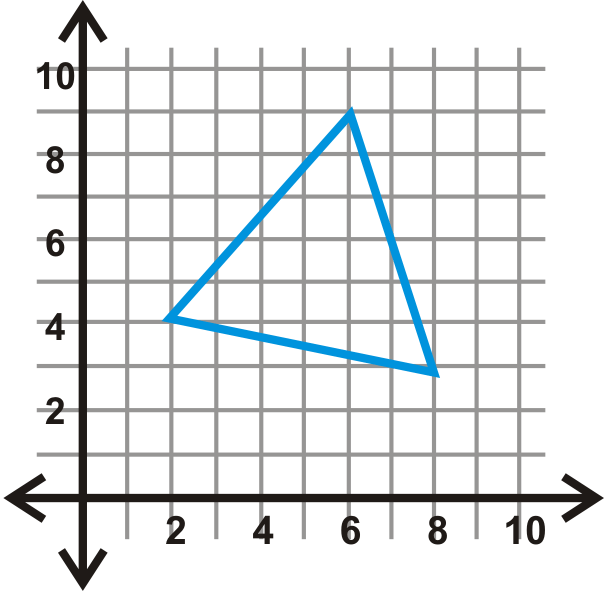
Figura\(\PageIndex{19}\) - \(x=−1\)
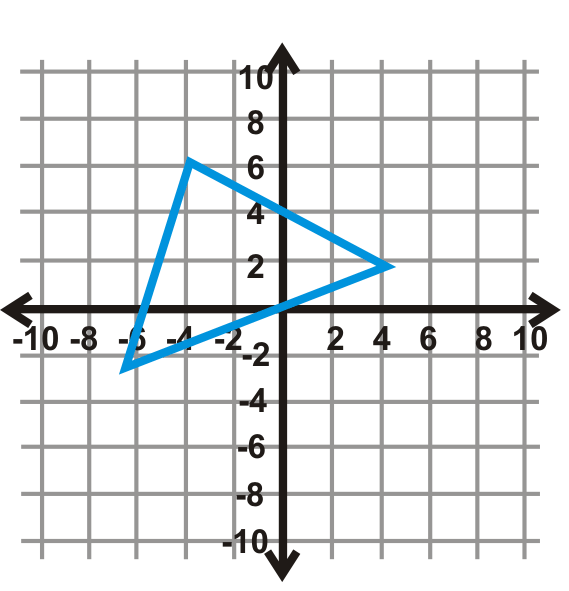
Figura\(\PageIndex{20}\) - \(x\)-eje
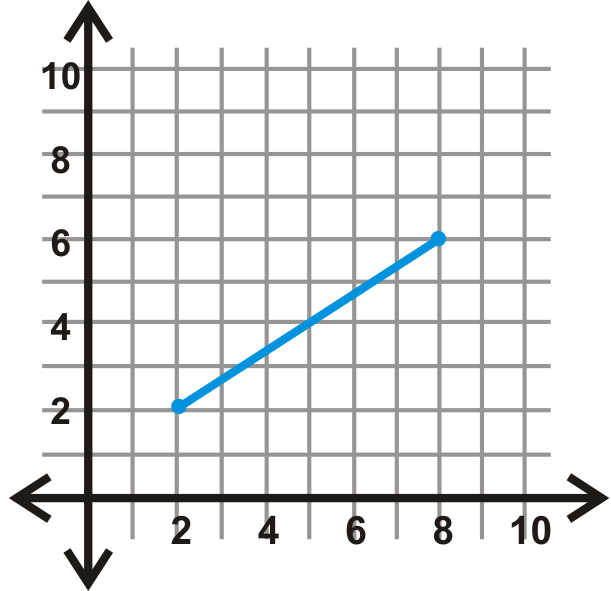
Figura\(\PageIndex{21}\) - \(y\)-eje
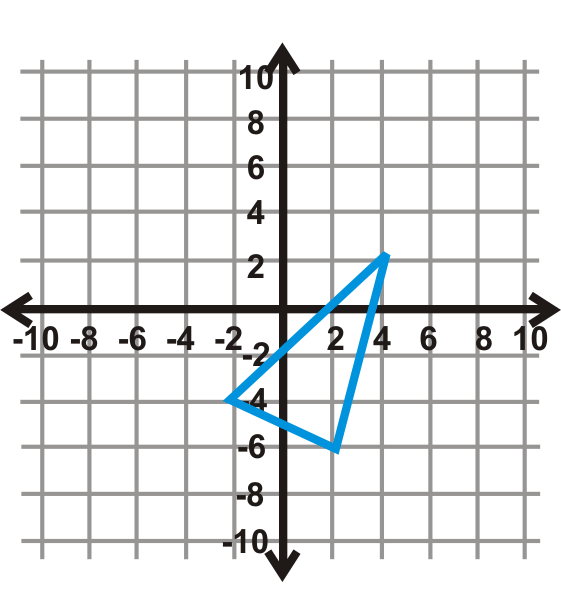
Figura\(\PageIndex{22}\) - \(y=x \)

Figura\(\PageIndex{23}\) - \(y=−x \)

Figura\(\PageIndex{24\) - \(x=2 \)

Figura\(\PageIndex{25}\) - \(y=−4 \)

Figura\(\PageIndex{26}\) - \(y=−x \)

Figura\(\PageIndex{27}\) - \(y=x \)

Figura\(\PageIndex{28}\)
Encuentra la línea de reflexión el triángulo azul (preimagen) y el triángulo rojo (imagen).
-
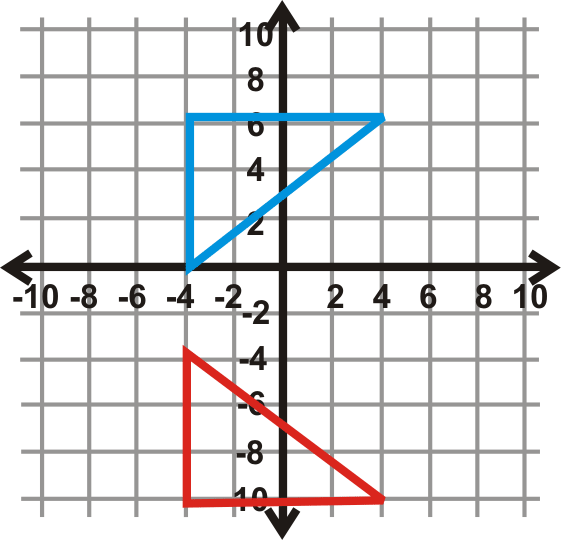
Figura\(\PageIndex{29}\) -
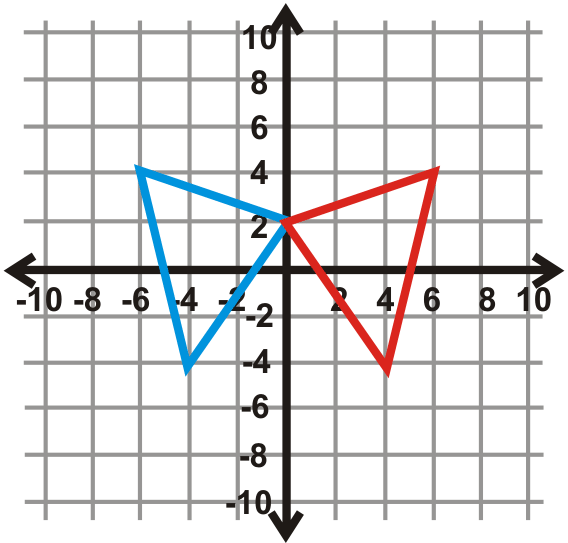
Figura\(\PageIndex{30}\) -
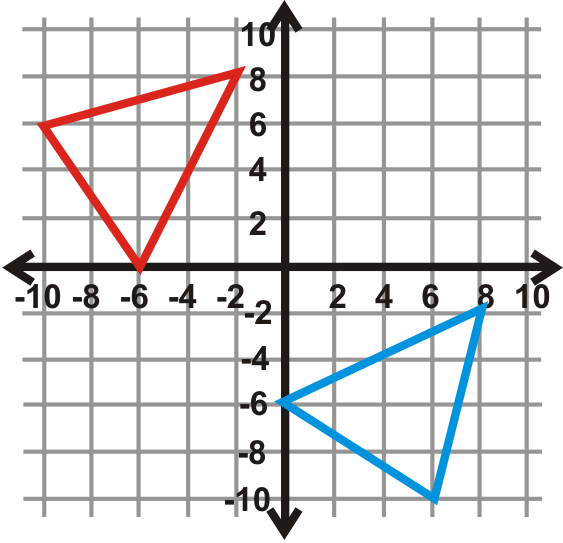
Figura\(\PageIndex{31}\)
El vocabulario
| Término | Definición |
|---|---|
| Plano de coordenadas | El plano de coordenadas es una rejilla formada por una recta numérica horizontal y una recta numérica vertical que se cruzan en el\((0, 0)\) punto, denominado origen. El plano de coordenadas también se llama Plano Cartesiano. |
| Patrones Geométricos | Los patrones geométricos son patrones visuales de figuras geométricas que siguen una regla. |
| Imagen | La imagen es la apariencia final de una figura después de una operación de transformación. |
| bisectriz perpendicular | Una bisectriz perpendicular de un segmento de línea pasa a través del punto medio del segmento de línea e intersecta el segmento de línea en\(90^{\circ}\). |
| Líneas perpendiculares | Las líneas perpendiculares son líneas que se cruzan en\(90^{\circ}\) ángulo. |
| Preimagen | La pre-imagen es la apariencia original de una figura en una operación de transformación. |
| Reflexión | Una reflexión es una transformación que voltea una figura en el plano de coordenadas a través de una línea dada sin cambiar la forma o el tamaño de la figura. |
| Transformación | Una transformación mueve una figura de alguna manera en el plano de coordenadas. |
| Transformación Rígida | Una transformación rígida es una transformación que conserva la distancia y los ángulos, no cambia el tamaño ni la forma de la figura. |
Reseña (Respuestas)
Para ver las respuestas de Revisar, abra este archivo PDF y busque la sección 12.5.
Recursos adicionales
Elemento Interactivo
Video: Transformación: Principios de Reflexión - Básicos
Actividades: Reflexiones Discusión Preguntas
Ayudas de estudio: Guía de estudio de tipos de transformaciones
Práctica: Definir la reflexión
Mundo Real: Reflejando la Realidad

