8.11: Reglas de Rotación
- Page ID
- 107599
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\(\newcommand{\longvect}{\overrightarrow}\)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Reglas estatales que describen rotaciones dadas.
Reglas para Rotaciones
La siguiente figura muestra un patrón de dos peces. Escriba la regla de mapeo para la rotación de la Imagen A a la Imagen B.
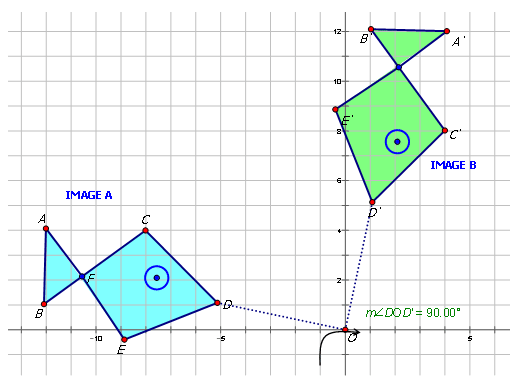
En geometría, una transformación es una operación que mueve, voltea o cambia una forma para crear una nueva forma. Una rotación es un ejemplo de una transformación donde una figura se gira alrededor de un punto específico (llamado centro de rotación), un cierto número de grados. Las rotaciones comunes sobre el origen se muestran a continuación:
| Centro de Rotación | Ángulo de rotación | Preimagen (Punto P) | Imagen Girada (Punto P′) | Notación (Punto P′) |
|---|---|---|---|---|
| (0, 0) | \(90^{\circ}\)(o\(−270^{\circ}\)) | \((x,y)\) | \((−y,x)\) | \((x,y)\rightarrow (−y,x)\) |
| (0, 0) | \(180^{\circ}\)(o\(−180^{\circ}\)) | \((x,y)\) | \((−x,−y)\) | \((x,y)\rightarrow (−x,−y)\) |
| (0, 0) | \(270^{\circ}\)(o\(−90^{\circ}\)) | \((x,y)\) | \((y,−x)\) | \((x,y)\rightarrow (y,−x)\) |
Se pueden describir las rotaciones en palabras, o con notación. Considera la imagen de abajo:
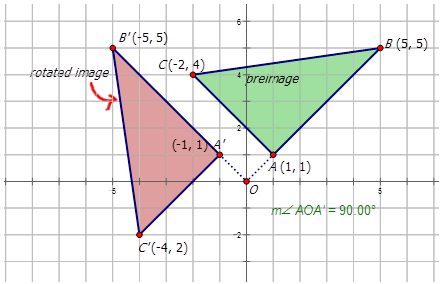
Observe que la preimagen se gira alrededor de la\(90^{\circ}\) CCW de origen. Si describieras la imagen rotada usando notación, escribirías lo siguiente:
\(R_{90^{\circ}}(x,y)=(−y,x)\)
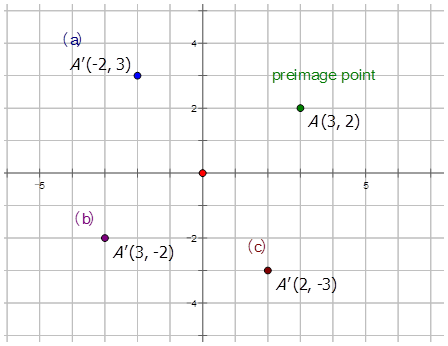
Escribamos la notación para describir las siguientes rotaciones CCW en el punto (3, 2)\) y dibujemos la imagen:
- sobre el origen en\(90^{\circ}\)
Rotación sobre el origen en\(90^{\circ}: \(R_{90^{\circ}}(x,y)=(−y,x)\)
- sobre el origen en\(180^{\circ}\)
Rotación sobre el origen en\(180^{\circ}\):\(R_{180^{\circ}}(x,y)=(−x, −y)\)
- sobre el origen en\(270^{\circ}\)
Rotación sobre el origen en 270^ {\ circ}:\(R_270^{\circ}(x,y)=(y,−x)\)
Ahora vamos a realizar las siguientes rotaciones en la imagen que\(A\) se muestra a continuación en el diagrama a continuación y describamos las rotaciones:
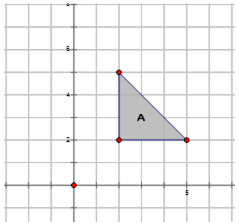
- sobre el origen en\(90^{\circ}\), y etiquetarlo\(B\).
Rotación sobre el origen en\(90^{\circ}\):\(R_{90^{\circ}}A\rightarrow B=R_{90^{\circ}}(x,y)\rightarrow (−y,x)\)
- sobre el origen en\(180^{\circ}\), y etiquetarlo\(O\).
Rotación sobre el origen en\(180^{\circ}\):\(R_{180^{\circ}}A\rightarrow O=R_{180^{\circ}}(x,y)\rightarrow (−x,−y)\)
- sobre el origen en\(270^{\circ}\), y etiquetarlo\(Z\).
Rotación sobre el origen en\(270^{\circ}\):\(R_{270^{\circ}}A\rightarrow Z=R270^{\circ}(x,y)\rightarrow (y,−x)\)
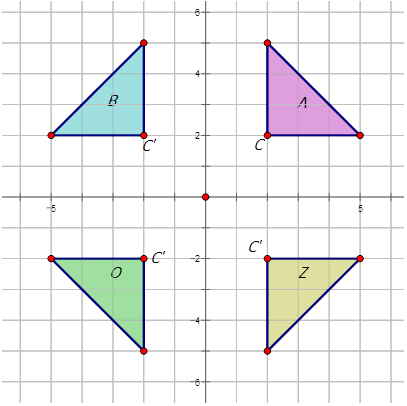
Finalmente, escribamos la notación que representa la rotación de la preimagen A a la imagen girada J en el diagrama siguiente:
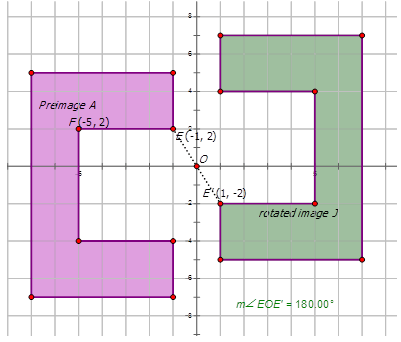
Primero, elige un punto en el diagrama para usar para ver cómo se gira.
\(E:(−1,2)\qquad E′:(1,−2)\)
Observe cómo las\(y\) coordenadas\(x\) - y -se multiplican por -1. Esto indica que la preimagen\(A\) se refleja sobre el origen por\(180^{\circ}\) CCW para formar la imagen rotada J. Por lo tanto la notación es\(R_{180^{\circ}}A\rightarrow J=R_{180^{\circ}}(x,y)\rightarrow (−x,−y)\).
Ejemplo\(\PageIndex{1}\)
Anteriormente, se le dio la siguiente figura que muestra un patrón de dos peces. Escribe la regla de mapeo para la rotación de Imagen\(A\) a Imagen\(B\).

Solución
Observe que la medida del ángulo es\(90^{\circ}\) y la dirección es en sentido horario. Por lo tanto, la Imagen se\(A\) ha rotado\(−90^{\circ}\) para formar Imagen\(B\). Para escribir una regla para esta rotación escribirías:\(R_{270^{\circ}}(x,y)=(−y,x)\).
Ejemplo\(\PageIndex{}\)
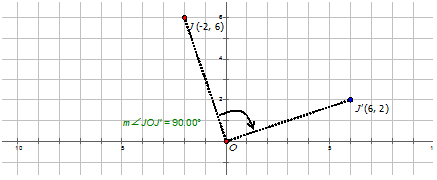
Thomas describe una rotación como punto que\(J\) se mueve de\(J(−2,6)\) a\(J′(6,2)\). Escribe la notación para describir esta rotación para Thomas.
\(J:(−2,6)\qquad J′:(6,2)\)
Solución
Dado que la\(x\) coordenada -se multiplica por -1, la\(y\) coordenada -permanece igual, y finalmente las\(y\) coordenadas\(x\) - y -cambian de lugar, esta es una rotación sobre el origen por\(270^{\circ}\) o\(−90^{\circ}\). La notación es:\(R_{270^{\circ}}J\rightarrow J′=R_270^{\circ}(x,y)\rightarrow (y,−x)\)
Ejemplo\(\PageIndex{1}\)
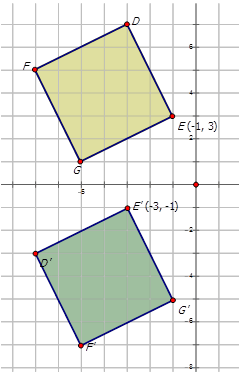
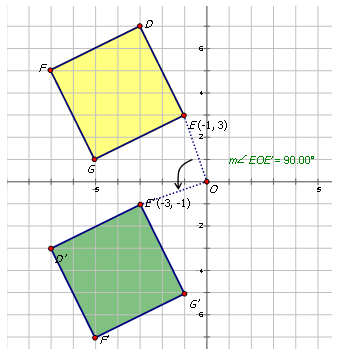
Escribe la notación que representa la rotación del diamante amarillo al diamante verde girado en el diagrama de abajo.
Solución
Para escribir la notación para describir la rotación, elija un punto en la preimagen (el diamante amarillo) y luego el punto girado en el diamante verde para ver cómo se ha movido el punto. Observe que el punto E\) se muestra en el diagrama:
\(E(−1,3)\rightarrow E′(−3,−1)\)
Dado que ambas\(y\) coordenadas\(x\) - y -son lugares invertidos y la\(y\) coordenada se ha multiplicado por -1, la rotación es sobre el origen\(90^{\circ}\). La notación para esta rotación sería:\(R_{90^{\circ}}(x,y)\rightarrow (−y,x)\).
Ejemplo\(\PageIndex{1}\)
Karen estaba jugando con un programa de dibujo en su computadora. Ella creó los siguientes diagramas y luego quiso determinar las transformaciones. Escribe la regla de notación que representa la transformación del diagrama púrpura y azul al diagrama naranja y azul.
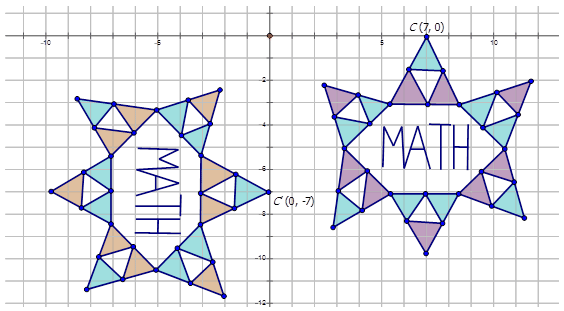
Solución
Para escribir la notación para describir la transformación, elija un punto en la preimagen (diagrama púrpura y azul) y luego el punto transformado en el diagrama naranja y azul para ver cómo se ha movido el punto. Observe que el punto\(C\) se muestra en el diagrama:
\(C(7,0)\rightarrow C′(0,−7)\)
Dado que las\(x\) -coordenadas sólo se multiplican por -1, y luego\(x\) - y\(y\) -coordenadas cambian de lugar, la transformación es una rotación es sobre el origen por\(270^{\circ}\). La notación para esta rotación sería:\(R_{270^{\circ}}(x,y)\rightarrow (y,−x)\).
Revisar
Complete la siguiente tabla:
| Punto de partida | \(90^{\circ}\)Rotación | \(180^{\circ}\)Rotación | \(270^{\circ}\)Rotación | \(360^{\circ}\)Rotación |
|---|---|---|---|---|
| 1. \((1, 4)\) | \ (90^ {\ circ}\) Rotación” class="lt-k12-6036"> | \ (180^ {\ circ}\) Rotación” class="lt-k12-6036"> | \ (270^ {\ circ}\) Rotación” class="lt-k12-6036"> | \ (360^ {\ circ}\) Rotación” class="lt-k12-6036"> |
| 2. \((4, 2)\) | \ (90^ {\ circ}\) Rotación” class="lt-k12-6036"> | \ (180^ {\ circ}\) Rotación” class="lt-k12-6036"> | \ (270^ {\ circ}\) Rotación” class="lt-k12-6036"> | \ (360^ {\ circ}\) Rotación” class="lt-k12-6036"> |
| 3. \((2, 0)\) | \ (90^ {\ circ}\) Rotación” class="lt-k12-6036"> | \ (180^ {\ circ}\) Rotación” class="lt-k12-6036"> | \ (270^ {\ circ}\) Rotación” class="lt-k12-6036"> | \ (360^ {\ circ}\) Rotación” class="lt-k12-6036"> |
| 4. \((-1, 2)\) | \ (90^ {\ circ}\) Rotación” class="lt-k12-6036"> | \ (180^ {\ circ}\) Rotación” class="lt-k12-6036"> | \ (270^ {\ circ}\) Rotación” class="lt-k12-6036"> | \ (360^ {\ circ}\) Rotación” class="lt-k12-6036"> |
| 5. \((-2, -3)\) | \ (90^ {\ circ}\) Rotación” class="lt-k12-6036"> | \ (180^ {\ circ}\) Rotación” class="lt-k12-6036"> | \ (270^ {\ circ}\) Rotación” class="lt-k12-6036"> | \ (360^ {\ circ}\) Rotación” class="lt-k12-6036"> |
Escribe la notación que representa la rotación de la preimagen a la imagen para cada diagrama a continuación.
-
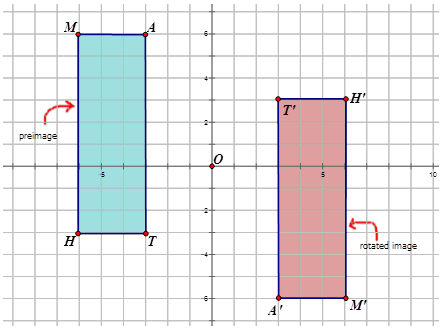
Figura\(\PageIndex{12}\) -
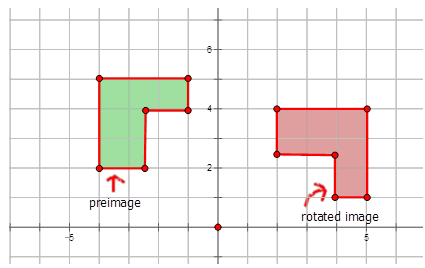
Figura\(\PageIndex{13}\) -
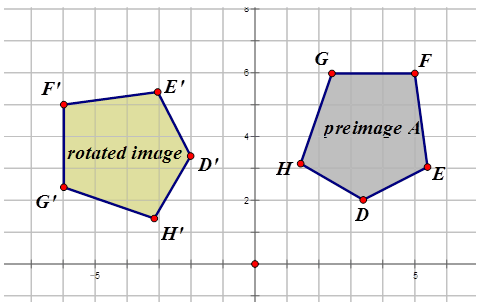
Figura\(\PageIndex{14}\) -
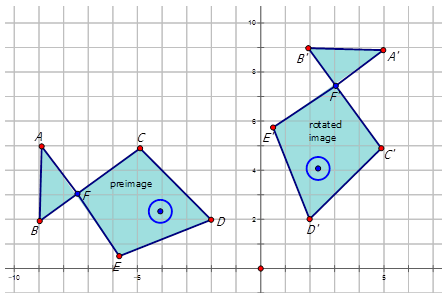
Figura\(\PageIndex{15}\) -
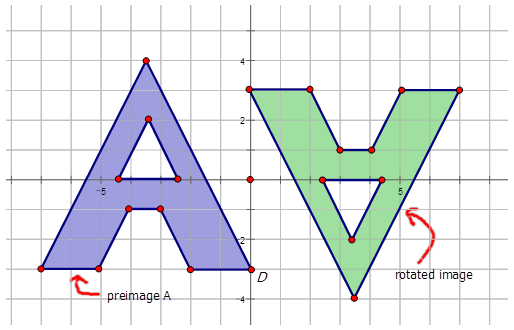
Figura\(\PageIndex{16}\)
Escribe la notación que representa la rotación de la preimagen a la imagen para cada diagrama a continuación.
-
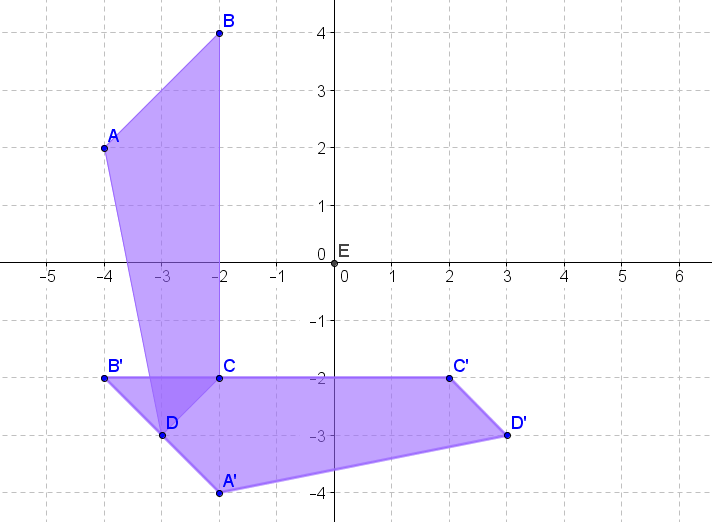
Figura\(\PageIndex{17}\) -
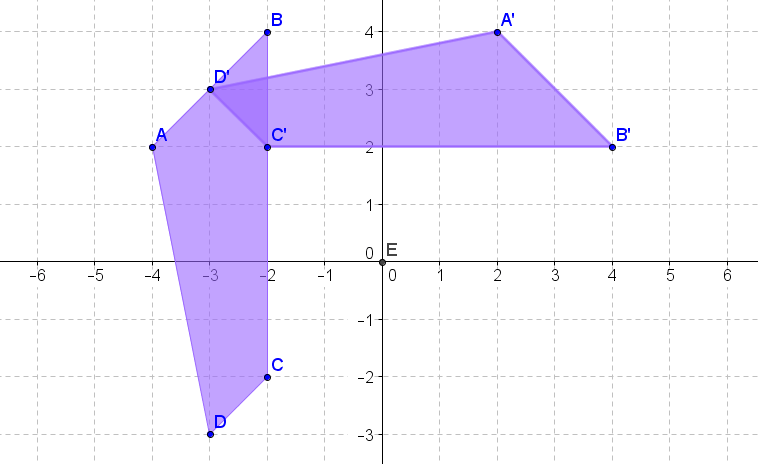
Figura\(\PageIndex{18}\) -
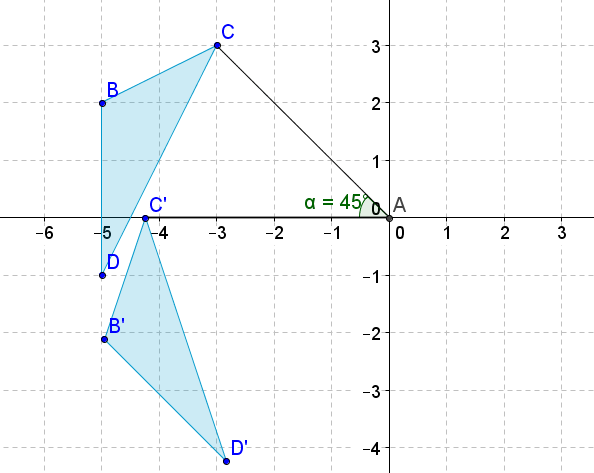
Figura\(\PageIndex{19}\) -
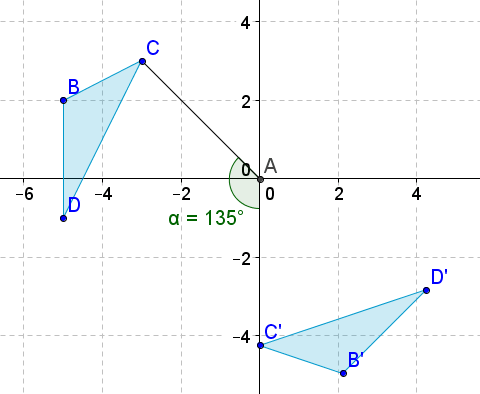
Figura\(\PageIndex{20}\) -
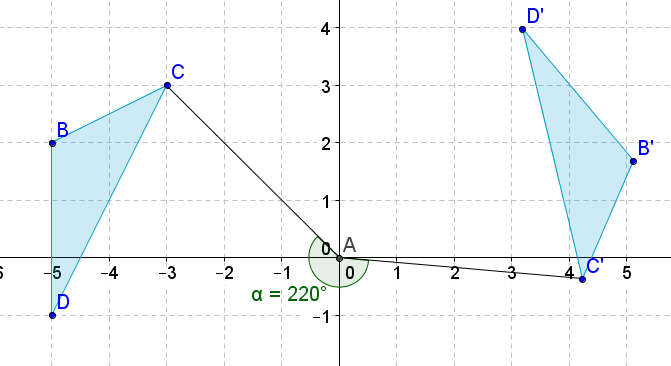
Figura\(\PageIndex{21}\)
Reseña (Respuestas)
Para ver las respuestas de Revisar, abra este archivo PDF y busque la sección 10.9.
Recursos adicionales
Video: Reglas para Rotaciones
Práctica: Reglas de rotación

