1.7:1.7 Aumentando y disminuyendo
- Page ID
- 107317
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Es importante poder distinguir entre cuándo las funciones están aumentando y cuándo están disminuyendo. En los negocios esto podría significar la diferencia entre ganar dinero y perder dinero. En física podría significar la diferencia entre acelerar y desacelerar.
¿Cómo decides cuándo una función está aumentando o disminuyendo?
Funciones crecientes y decrecientes
El aumento de medias coloca en la gráfica donde la pendiente es positiva.
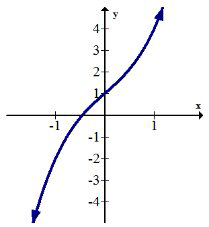
La definición formal de un intervalo creciente es: un intervalo abierto en el\(x\) eje de\((a, d)\) donde cada\(b, c \in(a, d)\) con\(b<c\) tiene\(f(b) \leq f(c)\)
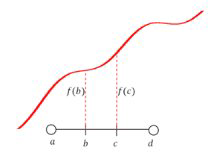
Se dice que un intervalo aumenta estrictamente si\(f(b)<f(c)\) se sustituye en la
definición.
Las medias decrecientes colocan en la gráfica donde la pendiente es negativa. La definición formal de decreciente y estrictamente decreciente son idénticas a la definición de aumentar con el signo de desigualdad invertido.
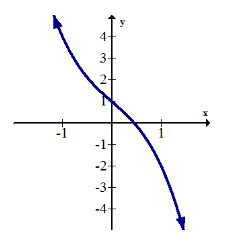
Una función se llama monotónica si la función solo va en una dirección y nunca cambia entre aumentar y disminuir.
Fuera de las funciones básicas, las funciones monótonamente crecientes son:
\(f(x)=x, f(x)=x^{3}, f(x)=\sqrt{x}, f(x)=e^{x}, f(x)=\ln x, f(x)=\frac{1}{1+e^{-x}}\)
Las únicas funciones básicas que no están aumentando monótonamente son:
\(f(x)=x^{2}, f(x)=|x|, f(x)=\frac{1}{x}, f(x)=\sin x\)
Identificar analíticamente dónde las funciones están aumentando y disminuyendo a menudo requiere Cálculo. Para Precálculo, será suficiente para poder identificar intervalos gráficamente y a través de tu conocimiento de cómo son las funciones padre.
Ejemplos
Anteriormente, se le preguntó cómo determinar si una función está aumentando o disminuyendo. Incrementar es donde la función tiene una pendiente positiva y decreciente es donde la función tiene una pendiente negativa. Un error común es mirar la función de cuadratura y ver dos curvas que aumentan simétricamente lejos de cero. En cambio, siempre debes leer las funciones de izquierda a derecha y dibujar líneas de pendiente y decidir si son positivas o negativas.
Estimar donde la siguiente función es cada vez mayor y decreciente.
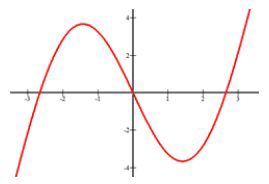
Incrementando:\(x \in(-\infty,-1.5) \cup(1.5, \infty)\).
Disminución:\(x \in(-1.5,1.5)\)
Estimar donde la siguiente función es cada vez mayor y decreciente.
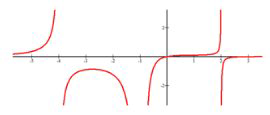
Incrementando\(x \in(-\infty,-4) \cup(-4,-2.7) \cup(-1,2) \cup(2, \infty)\).
Disminuyendo\(x \in(-2.7,-1)\)
Estimar los intervalos donde la función está aumentando y disminuyendo.
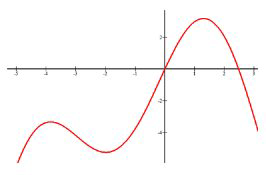
Creciente:\(x \in(-\infty,-4) \cup(-2,1.5)\)
Disminuyendo:\(x \in(-4,-2) \cup(1.5, \infty)\)
Observe que se utilizan intervalos abiertos porque en\(x=-4,-2,1.5\) la pendiente de la función es cero. Esto es aquí la pendiente transita de ser positiva a negativa. La razón por la que se utilizan paréntesis abiertos es porque la función en realidad no está aumentando o disminuyendo en esos puntos específicos.
Una función continua tiene un máximo global en el punto (3, 2), un mínimo global en (5, -12) y no tiene extremos relativos u otros lugares con una pendiente de cero. ¿Cuáles son los intervalos crecientes y decrecientes para esta función?
Incrementando\(x \in(-\infty, 3) \cup(5, \infty)\).
Disminuyendo\(x \in(3,5)\)
Nota: Las\(y\) coordenadas no se utilizan en los intervalos. Un error común es querer usar las\(y\) coordenadas.
Revisar
Utilice la gráfica a continuación para 1-2.
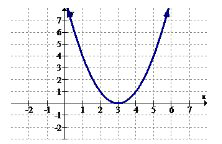
1. Identificar los intervalos (si los hay) donde la función está aumentando.
2. Identificar los intervalos (si los hay) donde la función está disminuyendo.
Utilice la gráfica de abajo para 3-4.
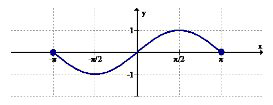
3. Identificar los intervalos (si los hay) donde la función está aumentando.
4. Identificar los intervalos (si los hay) donde la función está disminuyendo.
Utilice la gráfica de abajo para 5-6.
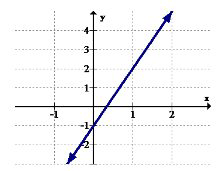
5. Identificar los intervalos (si los hay) donde la función está aumentando.
6. Identificar los intervalos (si los hay) donde la función está disminuyendo.
Utilice la gráfica de abajo para 7-8.
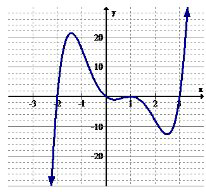
7. Identificar los intervalos (si los hay) donde la función está aumentando.
8. Identificar los intervalos (si los hay) donde la función está disminuyendo.
Utilice la gráfica de abajo para 9-10.
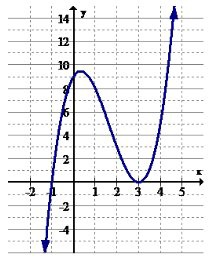
9. Identificar los intervalos (si los hay) donde la función está aumentando.
10. Identificar los intervalos (si los hay) donde la función está disminuyendo.
11. Dar un ejemplo de una función monótonamente creciente.
12. Dar un ejemplo de una función monótonamente decreciente.
13. Una función continua tiene un máximo global en el punto (1, 4), un mínimo global en (3, -6) y no tiene extremos relativos u otros lugares con una pendiente de cero. ¿Cuáles son los intervalos crecientes y decrecientes para esta función?
14. Una función continua tiene un máximo global en el punto (1, 1) y no tiene otros extremos o lugares con una pendiente de cero. ¿Cuáles son los intervalos crecientes y decrecientes para esta función?
15. Una función continua tiene un mínimo global en el punto (5, -15) y no tiene otros extremos o lugares con una pendiente de cero. ¿Cuáles son los intervalos crecientes y decrecientes para esta función?