1.11:1.11 Composición de la función
- Page ID
- 107353
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Las funciones se pueden sumar, restar, multiplicar y dividir creando nuevas funciones y gráficas que son combinaciones complicadas de las diversas funciones originales. Una forma importante de transformar funciones es a través de la composición de funciones. La composición de funciones permite alinear dos o más funciones que actúan sobre una entrada en tándem.
¿La composición de funciones es esencialmente lo mismo que multiplicar las dos funciones juntas?
Composición de las funciones
Una forma común de describir funciones es un mapeo desde el espacio de dominio al espacio de rango:
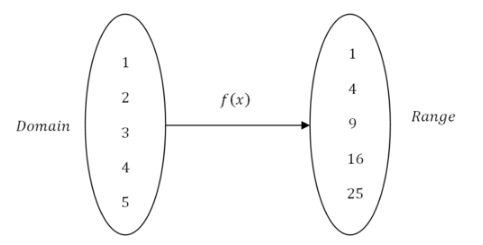
Composición de funciones significa que tienes dos o más funciones y el rango de la primera función se convierte en el dominio de la segunda función.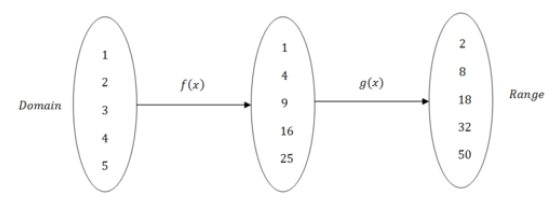 
Hay dos notaciones utilizadas para describir la composición de funciones. En cada caso el orden de las funciones importa porque aritméticamente los resultados serán diferentes. Al cuadrar un número y luego duplicar el resultado será diferente de duplicar un número y luego cuadrar el resultado. En el diagrama anterior,\(f(x)\) ocurre primero y\(g(x)\) ocurre segundo. Esto se puede escribir como:
\(g(f(x))\)o\((g \circ f)(x)\)
Deberías leer este "\(g\)\(f\)de”\(x\). En ambos casos notamos que el\(f\) está más cerca del
\(x\) y opera primero sobre los\(x\) valores.
Ejemplos
Anteriormente, se le preguntó si la composición de funciones es lo mismo que multiplicar dos funciones juntas. La composición de funciones no es lo mismo que multiplicar dos funciones juntas. Con la composición de funciones hay una función externa y una función interna. Supongamos que las dos funciones fueron duplicar y cuadrar. Está claro con solo mirar la entrada de ejemplo del número 5 que 50 (cuadrar luego duplicar) es diferente de 100 (duplicar luego cuadrar). Tanto 50 como 100 son ejemplos de composición de funciones, mientras que 250 (cinco duplicados multiplicados por cinco al cuadrado) es un ejemplo del producto de dos funciones separadas que suceden simultáneamente.
Para los siguientes dos ejemplos, use las siguientes funciones:
\(f(x)=x^{2}-1\)
\(h(x)=\frac{x-1}{x+5}\)
\(g(x)=3 e^{x}-x\)
\(j(x)=\sqrt{x+1}\)
Mostrar\(f(h(x)) \neq h(f(x))\)
\(f(h(x))=f\left(\frac{x-1}{x+5}\right)=\left(\frac{x-1}{x+5}\right)^{2}-1\)
\(h(f(x))=h\left(x^{2}-1\right)=\frac{\left(x^{2}-1\right)-1}{\left(x^{2}-1\right)+5}=\frac{x^{2}-2}{x^{2}+4}\)
Para demostrar verdaderamente que no son iguales lo mejor es encontrar un ejemplo de contador específico de un número donde difieran. A veces las expresiones algebraicas pueden verse diferentes, pero en realidad son las mismas. Deberías notar que\(f(h(x))\) está indefinido cuando\(x=-5\) porque entonces habría cero en el denominador. \(h(f(x))\)por otro lado se define en\(x=-5 .\) ya que las dos composiciones de funciones difieren, se puede concluir:
\(f(h(x)) \neq h(f(x))\)
Qué es\(f(j(h(g(x)))) ?\)
Estas funciones están anidadas dentro de los argumentos de las otras funciones. A veces las funciones se simplifican significativamente cuando se componen juntas, como\(f\) y\(j\) lo hacen en este caso. Tiene sentido evaluar esas dos funciones primero juntas y mantenerlas fuera del argumento.
\(f(x)=x^{2}-1 ; h(x)=\frac{x-1}{x+5} ; g(x)=3 e^{x}-x ; j(x)=\sqrt{x+1}\)
\(f(j(y))=f(\sqrt{y+1})=(\sqrt{y+1})^{2}-1=y+1-1=y\)
¿Observe cómo la composición de\(f\) y\(j\) produjo solo el argumento en sí?
Por lo tanto,
\(\begin{aligned} f(j(h(g(x))))=h(g(x)) &=h\left(3 e^{x}-x\right) \\ &=\frac{\left(3 e^{x}-x\right)-1}{\left(3 e^{x}-x\right)+5} \\ &=\frac{3 e^{x}-x-1}{3 e^{x}-x+5} \end{aligned}\)
Para los siguientes dos ejemplos, use las gráficas que se muestran a continuación:
\(f(x)=|x|\)
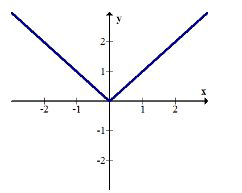
\(g(x)=e^{x}\)
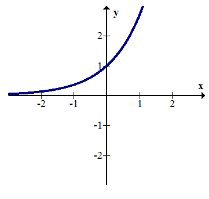
\(h(x)=-x\)
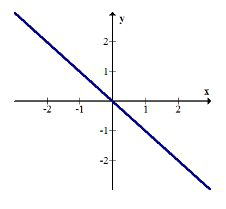
Redactar\(g(f(x))\) y graficar el resultado. Describir la transformación.
\(g(f(x))=g(|x|)=e^{|x|}\)
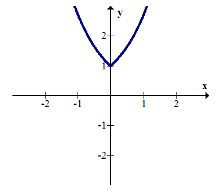
La porción positiva de la gráfica exponencial se ha reflejado sobre el\(y\) eje y la porción negativa de la gráfica exponencial se ha truncado por completo.
Redactar\(h(g(x))\) y graficar el resultado. Describir la transformación.
\(h(g(x))=h\left(e^{x}\right)=-e^{x}\)
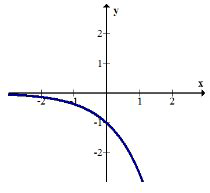
La gráfica exponencial se ha reflejado sobre el\(x\) eje.
Revisar
Para las preguntas 1-9, utilice las siguientes tres funciones:\(f(x)=|x|, h(x)=-x, g(x)=(x-2)^{2}-3\)
1. Gráfica\(f(x), h(x)\) y\(g(x)\).
2. Encuentra\(f(g(x))\) algebraicamente.
3. Grafica\(f(g(x))\) y describe la transformación.
4. Encuentra\(g(f(x))\) algebraicamente.
5. Grafica\(g(f(x))\) y describe la transformación.
6. Encuentra\(h(g(x))\) algebraicamente.
7. Grafica\(h(g(x))\) y describe la transformación.
8. Encuentra\(g(h(x))\) algebraicamente.
9. Grafica\(g(h(x))\) y describe la transformación.
Para 10-16, utilice las siguientes tres funciones:\(j(x)=x^{2}, k(x)=|x|, m(x)=\sqrt{x}\)
10. Gráfica\(j(x), k(x)\) y\(m(x)\).
11. Encuentra\(j(k(x))\) algebraicamente.
12. Grafica\(j(k(x))\) y describe la transformación.
13. Encuentra\(k(m(x))\) algebraicamente.
14. Grafica\(k(m(x))\) y describe la transformación.
15. Encuentra\(m(k(x))\) algebraicamente.
16. Grafica\(m(k(x))\) y describe la transformación.