1.12:1.12 Inversiones de funciones

Las funciones se conocen comúnmente como reglas que toman entradas y producen salidas. Una función i nverse hace exactamente lo contrario, deshaciendo lo que hace la función original. ¿Cómo se puede saber si dos funciones son inversas?

Encontrar inversos de funciones

Una función se escribe como$f(x)$ y su inversa se escribe como$f^{-1}(x)$. Un error común es ver el -1 e interpretarlo como exponente y escribir$\frac{1}{f(x)},$ pero esto no es correcto. En cambio,$f^{-1}(x)$ debe verse como una nueva función desde el rango de$f(x)$ regreso al dominio.

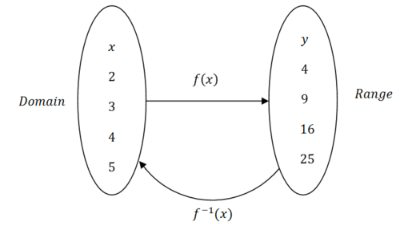
Es importante ver el ciclo que inicia con$x$, se convierte$y$ y luego vuelve a$x$. Para que dos funciones sean verdaderamente inversas entre sí, este ciclo debe sostenerse algebraicamente.

$f\left(f^{-1}(x)\right)=x$y$f^{-1}(f(x))=x$

Cuando se le da una función hay dos pasos a seguir para encontrar su inversa. En la función original, primero cambie las variables$x$ y$y$. A continuación, resolver la función para$y$. Esto te dará la función inversa. Después de encontrar la inversa, es importante verificar ambas direcciones de las composiciones para asegurarse de que juntas la función y su inversa produzcan el valor$x$. Es decir, verificar que$f\left(f^{-1}(x)\right)=x$ y$f^{-1}(f(x))=x$.

Gráficamente, las inversas son reflejos a través de la línea$y=x$. A continuación se ven inversos$y=e^{x}$ y$y=\ln x .$ Observe cómo las$(x, y)$ coordenadas en una gráfica se convierten en$(y, x)$ coordenadas en la otra gráfica.

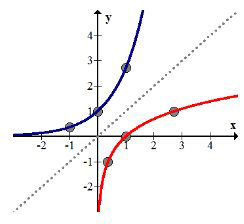
Para decidir si una función inversa también es realmente una función, puede usar la prueba de línea vertical en la función inversa como de costumbre. También puede usar la prueba de línea horizontal en la función original. La prueba de línea horizontal es exactamente igual que la prueba de línea vertical excepto que las líneas simplemente viajan horizontalmente.

Ejemplos

Ejemplo 1

Anteriormente, se le preguntó cómo se puede decir que dos funciones son inversas. Se puede decir que dos funciones son inversas si cada una deshace la otra, dejando siempre la original$x$.

Ejemplo 2

Encuentra la inversa, luego verifica la inversa algebraicamente. $f(x)=y=(x+1)^{2}+4$

Para encontrar la inversa, cambiar$x$ y$y$ luego resolver para$y$.

$\begin{aligned} x &=(y+1)^{2}+4 \\ x-4 &=(y+1)^{2} \\ \pm \sqrt{x-4} &=y+1 \\-1 \pm \sqrt{x-4} &=y=f^{-1}(x) \end{aligned}$

Para verificar algebraicamente, debes mostrar$x=f\left(f^{-1}(x)\right)=f^{-1}(f(x))$

$\begin{aligned} f\left(f^{-1}(x)\right) &=f(-1 \pm \sqrt{x-4}) \\ &=((-1 \pm \sqrt{x-4})+1)^{2}+4 \\ &=(\pm \sqrt{x-4})^{2}+4 \\ &=x-4+4=x \end{aligned}$

$\begin{aligned} f^{-1}(f(x)) &=f^{-1}\left((x+1)^{2}+4\right) \\ &=-1 \pm \sqrt{\left((x+1)^{2}+4\right)-4} \\ &=-1 \pm \sqrt{(x+1)^{2}} \\ &=-1+x+1=x \end{aligned}$

Como se puede ver en la gráfica, la$\pm$ causa que la inversa sea una relación en lugar de una función. Esto se puede observar en la gráfica porque la función original no pasa la prueba de línea horizontal y la inversa no pasa la prueba de línea vertical.

Ejemplo 3

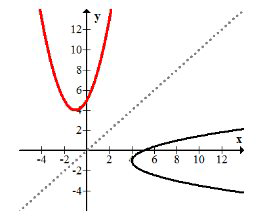
Encuentra la inversa de la función y luego verifica eso$x=f\left(f^{-1}(x)\right)=f^{-1}(f(x))$.

$f(x)=y=\frac{x+1}{x-1}$

A veces es bastante desafiante cambiar$x$$y$ y luego resolver por$y$. Debes tener cuidado con tu álgebra.

$\begin{aligned} x &=\frac{y+1}{y-1} \\ x(y-1) &=y+1 \\ x y-x &=y+1 \\ x y-y &=x+1 \\ y(x-1) &=x+1 \\ y &=\frac{x+1}{x-1} \end{aligned}$

Esta función resulta ser su propio inverso. ya que son idénticos, solo hace falta demostrar que$x=f\left(f^{-1}(x)\right)$

$f\left(\frac{x+1}{x-1}\right)=\frac{\left(\frac{x+1}{x-1}\right)+1}{\left(\frac{x+1}{x-1}\right)-1}=\frac{x+1+x-1}{x+1-(x-1)}=\frac{2 x}{2}=x$

Ejemplo 4

¿Cuál es la inversa de$f(x)=y=\sin x ?$

La función seno no pasa la prueba de línea horizontal y por lo tanto su verdadero inverso no es una función.

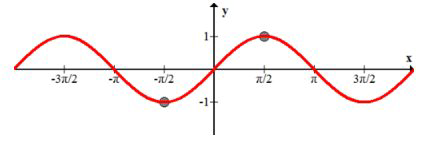
Sin embargo, si restringe el dominio a solo la parte del$x$ eje -entre$-\frac{\pi}{2}$ y$\frac{\pi}{2}$ entonces pasará la prueba de línea horizontal y la inversa será una función.

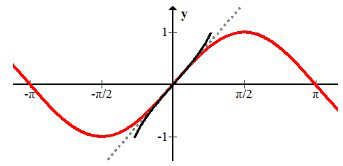
La inversa de la función sinusoidal se llama la función arcoseno,$f(x)=\sin ^{-1}(x),$ y se muestra en negro. Se trunca para que solo invierta una parte de toda la onda sinusoidal. Estudiarás las funciones periódicas y sus inversas con más detalle posteriormente.

Ejemplo 5

Determinar si$f(x)=\frac{3}{7} x-21$ y$g(x)=\frac{7}{3} x+21$ son inversos el uno del otro.

A pesar de$g(x)=\frac{7}{3} x+21$ que$f(x)=\frac{3}{7} x-21$ y tengan algunas piezas invertidas, no son inversas entre sí. Para mostrar esto, debes demostrar que la composición no simplifica a$x$.

$\frac{3}{7}\left(\frac{7}{3} x+21\right)-21=x+9-21=x-12 \neq x$

Revisar

Considerar$f(x)=x^{3}$

1. Sketch$f(x)$ y$f^{-1}(x)$.

2. Encuentra$f^{-1}(x)$ algebraicamente. ¿En realidad es una función?

3. Verificar algebraicamente que$f(x)$ y$f^{-1}(x)$ son inversos.

Considerar$g(x)=\sqrt{x}$.

4. Sketch$g(x)$ y$g^{-1}(x)$.

5. Encuentra$g^{-1}(x)$ algebraicamente. ¿En realidad es una función?

6. Verificar algebraicamente que$g(x)$ y$g^{-1}(x)$ son inversos.

Considerar$h(x)=|x|$

7. Sketch$h(x)$ y$h^{-1}(x)$.

8. Encuentra$h^{-1}(x)$ algebraicamente. ¿En realidad es una función?

9. Verificar gráficamente eso$h(x)$ y$h^{-1}(x)$ son inversos.

Considerar$j(x)=2 x-5$

10. Sketch$j(x)$ y$j^{-1}(x)$.

11. Encuentra$j^{-1}(x)$ algebraicamente. ¿En realidad es una función?

12. Verificar algebraicamente que$j(x)$ y$j^{-1}(x)$ son inversos.

13. Utilice la prueba de línea horizontal para determinar si la inversa de también$f(x)=x^{3}-2 x^{2}+1$ es una función.

14. ¿Son$g(x)=\ln (x+1)$ e$h(x)=e^{x-1}$ inversas? Explique.

15. Si se le dio una tabla de valores para una función, ¿cómo podría crear una tabla de valores para la inversa de la función?

c