2.11 Asíntotas oblicuas
- Page ID
- 107377
Cuando el grado del numerador de una función racional excede el grado del denominador por uno entonces la función tiene asíntotas oblicuas. Para encontrar estas asíntotas, es necesario utilizar la división polinómica larga y la porción no restante de la función se convierte en la asíntota oblicua. Una pregunta natural a hacer es: ¿qué sucede cuando el grado del numerador supera el del denominador por más de uno?
asíntotas oblicuas
Se muestra la siguiente función antes y después de que se realice la división polinómica larga.
\(f(x)=\frac{x^{4}+3 x^{2}+2 x+14}{x^{3}-3 x^{2}}=x+3+\frac{12 x^{2}+2 x+14}{x^{3}-3 x^{2}}\)
Observe que la porción restante irá a cero cuando\(x\) se vuelva extremadamente grande o extremadamente pequeña porque la potencia del numerador es menor que la potencia del denominador. Esto significa que si bien esta función puede volverse alocada con valores absolutos pequeños de\(x\), los valores absolutos grandes de\(x\) están extremadamente cerca de la línea\(y=x+3\).
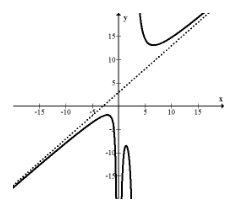
Las asíntotas oblicuas son estas asíntotas inclinadas que muestran exactamente cómo una función aumenta o disminuye sin límite. Las asíntotas oblicuas también se llaman asíntotas inclinadas.
En ocasiones una función tendrá una asíntota que no parece una línea. Eche un vistazo a la siguiente función:
\(f(x)=\frac{\left(x^{2}-4\right)(x+3)}{10(x-1)}\)
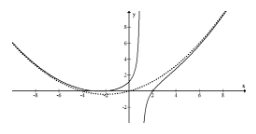
El grado del numerador es 3 mientras que el grado del denominador es 1 por lo que la asíntota inclinada no será una línea. Sin embargo, cuando se observa la gráfica, todavía hay un patrón claro en cuanto a cómo esta función aumenta sin límite a medida que\(x\) se acerca a números muy grandes y muy pequeños.
\(f(x)=\frac{1}{10}\left(x^{2}+4 x\right)-\frac{12}{10(x-1)}\)
Como pueden ver, esto parece una parábola con un resto. Esta función racional tiene una columna vertebral parábola. Una columna vertebral es una función a la que tiende una gráfica. Esto no es técnicamente una asíntota oblicua porque no es una línea.
Ejemplos
Antes, se le preguntó qué sucede cuando el poder del numerador supera en más de uno el poder del denominador. Como se vio anteriormente, cuando el poder del numerador excede el poder del denominador por más de uno, la función desarrolla una columna vertebral que se forma como cualquier polinomio. Las asíntotas oblicuas son siempre líneas.
Encuentra las asíntotas e intercepciones de la función:
\(f(x)=\frac{x^{3}}{x^{2}-4}\)
La función tiene asíntotas verticales en\(x=\pm 2\).
Después de una larga división, la función se convierte en:
\(f(x)=x+\frac{4}{x^{2}-4}\)
Esto hace que la asíntota oblicua en\(y=x\)
Identificar las asíntotas verticales y oblicuas de la siguiente función racional.
\ [
f (x) =\ frac {x^ {3} -x^ {2} -x-1} {(x-3) (x+4)}
\]
Después de usar la división larga polinomial y reescribir la función con una porción restante y no restante, se ve así:
\ [
f (x) =x-2+\ frac {13 x-25} {x^ {2} +x-12} =x-2+\ frac {13 x-25} {(x-3) (x+4)}
\]
La asíntota oblicua es\(y=x-2\). Las asíntotas verticales están en\(x=3\) y\(x=-4\) que son más fáciles de observar en última forma de la función porque claramente no cancelan para convertirse en agujeros.
Crear una función con una asíntota oblicua en asíntotas\(y=3 x-1,\) verticales en\(x=2,-4\) e incluye un agujero donde\(x\) es 7.
Si bien hay un número infinito de funciones que coinciden con estos criterios, un ejemplo es:
\ [
f (x) =3 x-1+\ frac {(x-7)} {(x-2) (x+4) (x-7)}
\]
Identificar la columna vertebral de la siguiente función y explicar por qué la función no tiene una asíntota oblicua.
\ [
f (x) =\ frac {5 x^ {5} +27} {x^ {3}}
\]
Si bien la división polinómica larga es posible, también es posible simplemente dividir cada término por\(x^{3}\).
\ [
f (x) =\ frac {5 x^ {5} +27} {x^ {3}} =\ frac {5 x^ {5}} {x^ {3}} +\ frac {27} {x^ {3}} =5 x^ {2} +\ frac {27} {x^ {3}}
\]
La columna vertebral de esta función es la parábola\(y=5 x^{2}\). Esto no es una asíntota oblicua porque no es una línea.
Revisar
1. ¿Qué es una asíntota oblicua?
2. ¿Cómo se puede saber mirando la ecuación de una función si va a tener una asíntota oblicua o no?
3. ¿Puede una función tener tanto una asíntota oblicua como una asíntota horizontal? Explique.
Para cada una de las siguientes gráficas, bosquejar la gráfica y luego bosquejar en la asíntota oblicua si existe. Si no existe, explique por qué no.
4.
5.
6.
7.
8.
Encuentra la ecuación de la asíntota oblicua para cada una de las siguientes funciones racionales. Si no hay una asíntota oblicua, explique por qué no y dé una ecuación de la columna vertebral de la función si existe una.
9. \(f(x)=\frac{x^{3}-7 x-6}{x^{2}-2 x-15}\)
10. \(g(x)=\frac{x^{3}-7 x-6}{x^{4}-3 x^{2}-10}\)
11. \(h(x)=\frac{x^{2}+5 x+6}{x^{2}+2 x+1}\)
12. \(k(x)=\frac{x^{4}+9 x^{3}+21 x^{2}-x-30}{x^{2}+2 x+1}\)
13. Crear una función con una asíntota oblicua en\(y=2 x-1,\) una asíntota vertical en\(x=3\) y un agujero donde\(x\) es 7.
14. Crea una función con una asíntota oblicua en\(y=x\), asíntotas verticales en\(x=1,-3\) y sin agujeros.
15. ¿Una parábola tiene una asíntota oblicua? ¿Qué pasa con una función cúbica?