2.4: Expresiones racionales
- Page ID
- 107384
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\(\newcommand{\longvect}{\overrightarrow}\)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Una expresión racional es una relación, igual que una fracción. Sin embargo, en lugar de una relación entre números, una expresión racional es una relación entre dos expresiones.
Una pregunta impulsora a hacer es: ¿Son las reglas para simplificar y operar sobre expresiones racionales las mismas que las reglas para simplificar y operar sobre fracciones?
Trabajar con expresiones racionales
Al simplificar u operar sobre expresiones racionales, es vital que cada polinomio sea plenamente factorizado. Una vez factorizadas todas las expresiones, se pueden cancelar o eliminar factores idénticos en el numerador y denominador. La razón por la que se pueden eliminar es que cualquier expresión dividida por sí misma es igual a 1. Una expresión idéntica en el numerador y denominador es solo una expresión que se divide por sí misma, y así es igual a 1.
Sumando y restando expresiones racionales
Para sumar o restar expresiones racionales, es fundamental encontrar primero un denominador común. Si bien cualquier denominador común funcionará, usar el mínimo denominador común es un medio para mantener bajo control el número de factores adicionales. Mira cada expresión racional con la que estás trabajando e identifica tu denominador común deseado. Multiplica cada expresión por una forma apropiada de 1, tal como\(\frac{x-2}{x-2}\), y entonces deberías tener tu denominador común. Además de los problemas de resta y suma, el numerador debe multiplicarse, combinarse y refactorizarse para que se considere simplificado.
Multiplicar y dividir expresiones racionales
Para multiplicar expresiones racionales, debes escribir el producto de todos los factores numeradores sobre el producto de todos los factores denominador y luego cancelar, o eliminar, factores idénticos.Para dividir expresiones racionales, debes reescribir el problema de división como un problema de multiplicación. Multiplicar la primera expresión racional por la recíproca de la segunda expresión racional. Siga los pasos anteriores para multiplicar. Tanto en los problemas de multiplicación como de división, las respuestas se dejan más comúnmente totalmente factorizadas para demostrar que todo se ha reducido adecuadamente.
Ejemplos
Anteriormente, se le preguntó si las reglas para simplificar y operar sobre expresiones racionales son las mismas que las reglas para simplificar y operar sobre fracciones. Las expresiones racionales son una extensión de fracciones y las operaciones de simplificar, sumar, restar, multiplicar y dividir funcionan exactamente de la misma manera.
Restar las siguientes expresiones racionales.
\(\frac{x-2}{x+3}-\frac{x^{3}-3 x^{2}+8 x-24}{2(x+2)\left(x^{2}-9\right)}\)
Ser capaz de factorizar de manera efectiva es de suma importancia.
\(=\frac{x-2}{x+3}-\frac{x^{3}-3 x^{2}+8 x-24}{2(x+2)\left(x^{2}-9\right)}\)
\(=\frac{(x-2)}{(x+3)}-\frac{x^{2}(x-3)+8(x-3)}{2(x+2)\left(x^{2}-9\right)}\)
\(=\frac{(x-2)}{(x+3)}-\frac{(x-3)\left(x^{2}+8\right)}{2(x+2)(x+3)(x-3)}\)
Antes de restar, simplifique cuando sea posible para que no contribuya a denominadores innecesariamente complicados.
\(=\frac{(x-2)}{(x+3)}-\frac{x^{2}+8}{2(x+2)(x+3)}\)
La expresión izquierda carece\(2(x+2)\), así que multiplica tanto su numerador como su denominador por\(2(x+2)\)
\(=\frac{2(x+2)(x-2)}{2(x+2)(x+3)}-\frac{\left(x^{2}+8\right)}{2(x+2)(x+3)}\)
\(=\frac{2\left(x^{2}-4\right)-x^{2}-8}{2(x+2)(x+3)}\)
\(=\frac{x^{2}-16}{2(x+2)(x+3)}\)
Simplificar la siguiente expresión racional.
\(\frac{x^{2}+7 x+12}{x^{2}+4 x+3} \cdot \frac{x^{2}+9 x+8}{2 x^{2}-128} \div \frac{x+4}{x-8} \cdot \frac{14}{1}\)
Primer factor todo. Segundo, convertir la división en multiplicación (sólo un término). Tercero, cancelar apropiadamente lo que dejará la respuesta.
\(=\frac{(x+3)(x+4)}{(x+3)(x+1)} \cdot \frac{(x+8)(x+1)}{2(x+8)(x-8)} \cdot \frac{(x-8)}{(x+4)} \cdot \frac{14}{1}\)
\(=\frac{(x+3)(x+4)}{(x+3)(x+1)} \cdot \frac{(x+8)(x+1)}{2(x+8)(x-8)} \cdot \frac{(x-8)}{(x+4)} \cdot \frac{14}{1}\)
\(=\frac{14}{2}\)
\(=7\)
En este ejemplo, se muestra el strike through. Debe utilizar esta técnica para hacer coincidir factores en el numerador y el denominador a la hora de simplificar.
Combina las siguientes expresiones racionales.
\(\frac{1}{x^{2}+5 x+6}-\frac{1}{x^{2}-4}+\frac{(x-7)(x+5)+5}{(x+2)(x-2)(x+3)(x-4)}\)
Primero factorizar todo y decidir sobre un denominador común. Si bien los numeradores realmente no necesitan ser factorizados, a veces es útil para simplificar las expresiones individuales antes de combinarlas. Tenga en cuenta que el numerador de la expresión en la mano derecha parece factorizado pero realmente no lo es. Dado que el 5 no está conectado con el resto del numerador a través de la multiplicación, esa parte de la expresión necesita ser multiplicada y es necesario combinar términos similares.
\(=\frac{1}{(x+2)(x+3)}-\frac{1}{(x+2)(x-2)}+\frac{x^{2}-2 x-35+5}{(x+2)(x-2)(x+3)(x-4)}\)
\(=\frac{1}{(x+2)(x+3)}-\frac{1}{(x+2)(x-2)}+\frac{x^{2}-2 x-30}{(x+2)(x-2)(x+3)(x-4)}\)
Tenga en cuenta que la expresión derecha tiene 4 factores en el denominador mientras que cada una de las expresiones de la izquierda tiene dos que coinciden y dos que faltan en esos cuatro factores. Esto te dice por qué necesitas multiplicar cada expresión para que los denominadores coincidan.
\(=\frac{(x-2)(x-4)}{(x+2)(x-2)(x+3)(x-4)}-\frac{(x+3)(x-4)}{(x+2)(x-2)(x+3)(x-4)}+\frac{x^{2}-2 x-30}{(x+2)(x-2)(x+3)(x-4)}\)
Ahora bien, como las expresiones racionales tienen un denominador común, los numeradores pueden multiplicarse y combinarse. A veces en lugar de reescribir una expresión repetidamente en matemáticas se puede usar una abreviatura. En este caso, se puede sustituir el denominador por la letra\(D\) y luego reemplazarlo al final.
\(=\frac{(x-2)(x-4)-(x+3)(x-4)+x^{2}-2 x-30}{D}\)
\(=\frac{x^{2}-6 x+8-\left[x^{2}-x-12\right]+x^{2}-2 x-30}{D}\)
Observe cómo es sumamente importante usar corchetes para indicar que la resta se aplica a todos los términos de la expresión media no solo\(x^{2}\). Este es uno de los errores más comunes.
\(=\frac{x^{2}-6 x+8-x^{2}+x+12+x^{2}-2 x-30}{D}\)
\(=\frac{x^{2}-7 x-10}{D}\)
Después de que el numerador se haya simplificado por completo intenta factorizar la expresión restante y ver si algo se cancela con el denominador que ahora necesitas reemplazar.
\(=\frac{(x+2)(x-5)}{(x+2)(x-2)(x+3)(x-4)}\)
\(=\frac{(x-5)}{(x-2)(x+3)(x-4)}\)
Simplifica la siguiente expresión.
\(\frac{\frac{1}{x+1}-\frac{1}{x+2}}{\frac{1}{x-2}-\frac{1}{x+1}}\)
La expresión en sí no parece una expresión racional, sino que se puede reescribir para que sea más reconocible. Además, trabajar con fracciones dentro de fracciones es una habilidad importante.
\(=\left(\frac{1}{x+1}-\frac{1}{x+2}\right) \div\left(\frac{1}{x-2}-\frac{1}{x+1}\right)\)
\(=\left[\frac{(x+2)}{(x+1)(x+2)}-\frac{(x+1)}{(x+1)(x+2)}\right] \div\left[\frac{(x+1)}{(x+1)(x-2)}-\frac{(x-2)}{(x+1)(x-2)}\right]\)
\(=\left[\frac{1}{(x+1)(x+2)}\right] \div\left[\frac{3}{(x+1)(x-2)}\right]\)
\(=\frac{1}{(x+1)(x+2)} \cdot \frac{(x+1)(x-2)}{3}\)
\(=\frac{(x-2)}{3(x+2)}\)
Simplifica la siguiente expresión que tiene un número infinito de fracciones anidadas dentro de otras fracciones.
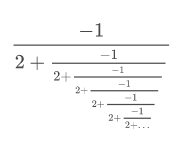
Sería un ejercicio de inutilidad intentar intentar computar esta expresión directamente. En cambio, observe que la naturaleza repetitiva de la expresión se presta a una sustitución extremadamente agradable.
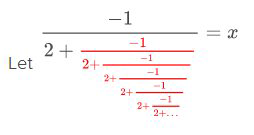
Observe que la porción roja de la fracción es exactamente la misma que el resto de la fracción y así\(x\) puede sustituirse ahí y resolverse.
\(\begin{aligned} \frac{-1}{2+x} &=x \\-1 &=x(2+x) \\-1 &=x^{2}+2 x \\ 0 &=x^{2}+2 x+1 \\ 0 &=(x+1)^{2} \\ x &=-1 \end{aligned}\)
La razón por la que esta expresión se incluye en este concepto es porque resalta un aspecto de resolución de problemas de la simplificación de expresiones que distingue Precálculo de Álgebra 1 y Álgebra 2.
Revisar
Realizar la operación indicada y simplificar en la medida de lo posible.
1. \(\frac{x^{2}+5 x+4}{x^{2}+4 x+3} \cdot \frac{5 x^{2}+15 x}{x+4}\)
2. \(\frac{x^{2}-4}{x^{2}+4 x+4} \cdot \frac{7}{x-2}\)
3. \(\frac{4 x^{2}-12 x}{5 x+10} \cdot \frac{x+2}{x} \div \frac{x-3}{1}\)
4. \(\frac{4 x^{3}-4 x}{x} \div \frac{2 x-2}{x-4}\)
5. \(\frac{2 x^{3}+8 x}{x+1} \div \frac{x}{2 x^{2}-2}\)
6. \(\frac{3 x-1}{x^{2}+2 x-15}-\frac{2}{x+5}\)
7. \(\frac{x^{2}-8 x+7}{x^{2}-4 x-21} \cdot \frac{x^{2}-9}{1-x^{2}}\)
8. \(\frac{2}{x+7}+\frac{1}{x-7}\)
9. \(\frac{6}{x-7}-\frac{6}{x+7}\)
10. \(\frac{3 x+35}{x^{2}-25}+\frac{2}{x+5}\)
11. \(\frac{2 x+20}{x^{2}-4 x-12}+\frac{2}{x+2}\)
12. \(\frac{2}{x+6}-\frac{x-9}{x^{2}-3 x-18}\)
13. \(-\frac{5 x+30}{x^{2}+11 x+30}+\frac{2}{x+5}\)
14. \(\frac{x+3}{x+2}+\frac{x^{3}+4 x^{2}+5 x+20}{2 x^{4}+2 x^{2}-40}\)
15. \(\frac{-4}{2+\frac{-4}{2+\frac{-4}{2+\frac{-4}{2+\frac{-4}{2+\frac{-4}{2+\cdots}}}}}}\)

