2.9 Aíntotas Verticales
- Page ID
- 107369
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\(\newcommand{\longvect}{\overrightarrow}\)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)La función racional básica\(f(x)=\frac{1}{x}\) es una hipérbola con una asíntota vertical en\(x=0\). Las funciones racionales más complicadas pueden tener múltiples asíntotas verticales. Estas asíntotas son características muy importantes de la función al igual que los agujeros. Tanto los agujeros como las asíntotas verticales ocurren en\(x\) valores que hacen que el denominador de la función sea cero. Una pregunta impulsora es: ¿qué hace que las asíntotas verticales sean diferentes de los agujeros?
Búsqueda de asíntotas verticales
Las asíntotas verticales ocurren cuando un factor del denominador de una expresión racional no se cancela con un factor del numerador. Cuando se tiene un factor que no cancela, en lugar de hacer un agujero a ese\(x\) valor, existe una asíntota vertical. La asíntota vertical está representada por una línea vertical punteada. La mayoría de las calculadoras no identificarán asíntotas verticales y algunas dibujarán incorrectamente una línea empinada como parte de una función donde realmente existe la asíntota.
Tu trabajo es poder identificar asíntotas verticales a partir de una función y describir cada asíntota usando la ecuación de una línea vertical.
Tome la siguiente función racional:
\(f(x)=\frac{(2 x-3)(x+1)(x-2)}{(x+2)(x+1)}\)
Para identificar los agujeros y las ecuaciones de las asíntotas verticales, primero decidir qué factores cancelan. El factor que cancela representa la discontinuidad removible. Hay un agujero en (-1,15). La asíntota vertical ocurre en\(x=-2\) porque el factor\(x+2\) no cancela.
Vea el siguiente video, enfocándose en las partes sobre asíntotas verticales.
Anteriormente, se le preguntó en qué se diferencian las asíntotas que los agujeros. Los agujeros ocurren cuando los factores del numerador y el denominador cancelan. Cuando un factor en el denominador no cancela, produce una asíntota vertical. Tanto los agujeros como las asíntotas verticales restringen el dominio de una función racional.
Escribe una función que se ajuste a los siguientes criterios:
- asíntotas verticales a 0 y 3
- Ceros a 2 y 5
- Agujero en (4, 2)
Cada criterio ayuda a construir la función. Las asíntotas verticales implican que el denominador tiene dos factores que no cancelan con el numerador:
\(\frac{1}{x \cdot(x-3)}\)
Los ceros a 2 y 5 implican que el numerador tiene dos factores que no cancelan.
\(\frac{(x-2)(x-5)}{x \cdot(x-3)}\)
El agujero en (4,2) implica que hay un factor\(x-4\) que cancela en el numerador y el denominador.
\(\frac{(x-2)(x-5)(x-4)}{x \cdot(x-3)(x-4)}\)
La parte complicada es que la altura de la función debe ser 2 después de que el\(x-4\) factor haya sido cancelado y el 4 sea sustituido en. Actualmente es\(-\frac{1}{2}\)
\(\frac{(4-2)(4-5)}{4 \cdot(4-3)}=-\frac{1}{2}\)
Para que el agujero exista a una altura de 2, es necesario multiplicar la función por un escalar de -4.
\(f(x)=\frac{-4(x-2)(x-5)(x-4)}{x \cdot(x-3)(x-4)}\)
Dibuja las asíntotas verticales para la siguiente función.
\(f(x)=\frac{1}{(x-4)(x-2)(x+3)}\)
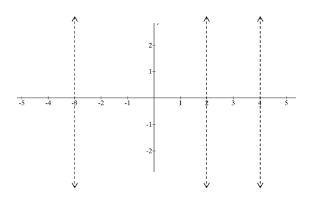
Tenga en cuenta que es posible que no conozca las características de lo que hace la función dentro de estas líneas verticales. Pronto aprenderás a usar pruebas de signos así como técnicas que ya aprendiste para rellenar las cuatro secciones en las que se divide esta función.
Identificar los agujeros y ecuaciones de las asíntotas verticales de la siguiente función racional.
\(f(x)=\frac{3(x-1)(x+2)(x-3)(x+4)}{5\left(x+\frac{1}{2}\right)(2+x)(3-x)(x-8)}\)
Las asíntotas verticales ocurren en\(x=-\frac{1}{2}, x=8 .\) Los agujeros ocurren cuando\(x\) es -2 y\(3 .\) Para obtener la altura de los agujeros en estos puntos, recuerde cancelar lo que se puede cancelar y luego sustituir los valores. Un error muy común es olvidar cancelar\(\frac{x-3}{3-x}=-1\)
\(\begin{aligned} g(x) &=\frac{-3(x-1)(x+4)}{5\left(x+\frac{1}{2}\right)(x-8)} \\ g(-2) &=\frac{6}{25} \\ g(3) &=\frac{12}{25} \end{aligned}\)
Los agujeros están en\(\left(-2, \frac{6}{25}\right),\left(3, \frac{12}{25}\right)\)
Identificar el dominio de la siguiente función y luego identificar los agujeros y asíntotas verticales.
\(f(x)=\frac{(3 x-4)(1-x)\left(x^{2}+4\right)}{(3 x-2)(x-1)}\)
El dominio de la función escrita en notación de intervalos es:\(\left(-\infty, \frac{2}{3}\right) \cup\left(\frac{2}{3}, 1\right) \cup(1, \infty) .\) Tenga en cuenta que el dominio es todo números reales excepto donde el denominador es cero.
Hay dos discontinuidades: una es un agujero y otra es una asíntota vertical. El agujero ocurre en (1,5) La asíntota vertical ocurre en\(x=\frac{2}{3}\)
Observe que los agujeros se identifican como puntos mientras que las asíntotas verticales se identifican como líneas de la forma
\(x=a\) donde\(a\) hay alguna constante.
Revisar
1. Escribe una función que se ajuste a los siguientes criterios:
- Aíntotas verticales en 1 y 4
- Ceros a 3 y 5
- Orificio en (6, 3)
2. Escribe una función que se ajuste a los siguientes criterios:
- asíntotas verticales a -2 y 2
- Ceros en 1 y 5
- Orificio en (3, -4)
3. Escribe una función que se ajuste a los siguientes criterios:
- asíntotas verticales a 0 y 3
- Ceros en 1 y 2
- Orificio en (8, 21)
4. Escribe una función que se ajuste a los siguientes criterios:
- Aíntotas verticales a las 2 y 6
- Cero a 5
- Orificio en (4, 1)
5. Escribe una función que se ajuste a los siguientes criterios:
- Aíntota vertical a las 4
- Ceros a 0 y 3
- Orificio en (5, 10)
Dar las ecuaciones de las asíntotas verticales para las siguientes funciones.
6. \(f(x)=\frac{(2-x)}{(x-2)(x-4)}\)
7. \(g(x)=\frac{-x}{(x+1)(x-3)}\)
8. \(h(x)=6-\frac{x+2}{(x+1)(x-5)}\)
9. \(j(x)=\frac{10}{x-3}-\frac{x}{(x+2)(x-3)}\)
10. \(k(x)=2-\frac{(4-x)}{(x+3)(x-4)}\)
Identificar los agujeros y ecuaciones de las asíntotas verticales de las siguientes funciones racionales.
11. \(f(x)=\frac{3(x-1)(x+1)(x-4)(x+4)}{4(x+4)(2+x)(4-x)(x+1)}\)
12. \(g(x)=\frac{x(x-3)(x-8)(x-3)(x+4)}{7(x+1)(1+x)(3-x)(x-8)}\)
Declarar el dominio de las siguientes funciones racionales.
13. \(h(x)=\frac{x(x+1)(x-3)(x+4)}{x(3-x)(x-1)}\)
14. \(j(x)=\frac{x^{2}+3 x-4}{x^{2}-6 x-16}\)
15. \(k(x)=\frac{2 x-10}{x^{3}+4 x^{2}+3 x}\)

