2.10 Asíntotas Horizontales
- Page ID
- 107370
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\(\newcommand{\longvect}{\overrightarrow}\)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Las asíntotas verticales describen el comportamiento de una función como los valores de\(x\) aproximación a un número específico. Las asíntotas horizontales describen el comportamiento de una función como los valores de\(x\) volverse infinitamente grandes e infinitamente pequeños. ya que las funciones no pueden tocar asíntotas verticales, ¿tampoco se les permite tocar asíntotas horizontales?
Búsqueda de asíntotas horizontales
Las asíntotas horizontales son un medio para describir el comportamiento final de una función. El comportamiento final esencialmente es una descripción de lo que sucede a cada lado de la gráfica a medida que la función continúa infinitamente hacia la derecha y hacia la izquierda. Al determinar las asíntotas horizontales, es importante considerar tanto el lado derecho como el izquierdo, ya que las asíntotas horizontales no necesariamente serán las mismas en ambos lugares. Considera la función recíproca y observa cómo como\(x\) va a la derecha y a la izquierda se aplana a la línea\(y=0\).
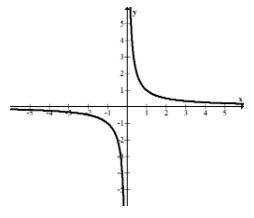
A veces las funciones se aplanan y otras veces las funciones aumentan o disminuyen sin límite. Básicamente hay tres casos.
Caso 1: El grado de numerador es menor que el grado de denominador
El primer caso es que la función se aplana a 0 ya que\(x\) se vuelve infinitamente grande o infinitamente pequeña. Esto sucede cuando el grado del numerador es menor que el grado del denominador. El grado está determinado por el mayor exponente de\(x\).
\(f(x)=\frac{2 x^{8}+3 x^{2}+100}{x^{9}-12}\)
Una forma de razonar por qué esto tiene sentido es porque cuando\(x\) es un número ridículamente grande entonces la mayoría de las partes de la función apenas tienen ningún impacto. El 100 por ejemplo no es nada en comparación y tampoco lo es el\(3 x^{2}\). Los dos términos importantes a comparar son\(x^{8}\) y\(x^{9}\). El 2 ni siquiera es importante ahora porque si\(x\) es solo un millón que el\(x^{9}\) será un millón de veces más grande que el\(x^{8}\) y el 2 apenas importa de nuevo. Esencialmente, cuando\(x\) se hace lo suficientemente grande, esta función actúa como\(\frac{1}{x}\) que tiene una asíntota horizontal de\(0 .\)
Caso 2: El grado de numerador es igual al grado de denominador
Si el grado del numerador es igual al grado del denominador, la asíntota horizontal es igual a la relación de los coeficientes iniciales.
\(f(x)=\frac{6 x^{4}-3 x^{3}+12 x^{2}-9}{3 x^{4}+144 x-0.001}\)
Observe como el grado tanto del numerador como del denominador es 4. Esto quiere decir que la asíntota horizontal es\(y=\frac{6}{3}=2\). Una forma de razonar por qué esto tiene sentido es porque cuando\(x\) llega a ser un número muy grande todas las potencias más pequeñas realmente no tendrán mucho impacto. Los mayores contribuyentes son sólo los mayores poderes. Entonces el valor del numerador será aproximadamente el doble que el del denominador. A medida que\(x\) se hace aún más grande, entonces la función se acercará aún más a 2.
Caso 3: El grado de numerador es mayor que el grado de denominador
Si el grado del numerador es mayor que el grado del denominador, no existe una asíntota horizontal. Debes determinar si la función aumenta o disminuye sin límite tanto en la dirección izquierda como en la derecha.
Vea el siguiente video, enfocándose en las partes sobre asíntotas horizontales.
Ejemplos
Anteriormente, se le preguntó si a las funciones se les permite tocar sus asíntotas horizontales. Las funciones pueden tocar y pasar por asíntotas horizontales sin límite. Esta es una diferencia entre asíntotas verticales y horizontales. En el cálculo, existen pruebas rigurosas para demostrar que funciones como la del Ejemplo C se acercan arbitrariamente a la asíntota.
Identificar las asíntotas verticales y horizontales de la siguiente función racional.
\(f(x)=\frac{(x-2)(4 x+3)(x-4)}{(x-1)(4 x+3)(x-6)}\)
Hay factor que cancela que no es ni una asíntota horizontal ni vertical. Las asíntotas verticales ocurren en\(x=1\) y\(x=6\). Para obtener la asíntota horizontal se podría multiplicar metódicamente cada binomio, sin embargo como la mayoría de esos términos no importan, es más eficiente determinar primero las potencias relativas del numerador y el denominador. En este caso ambos resultan ser 3. A continuación determinar el coeficiente de los términos cúbicos solamente. El numerador tendrá\(4 x^{3}\) y el denominador tendrá\(4 x^{3}\) y así la asíntota horizontal ocurrirá en\(y=\frac{4}{4}=1\)
Describir el comportamiento del extremo derecho de la siguiente función.
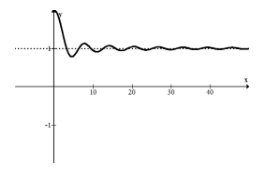
Observe la rapidez con la que se establece esta función de onda de amortiguación. Parece que hay un eje horizontal obvio a la derecha en\(y=1\)
Identificar las asíntotas horizontales de la siguiente función.
\(f(x)=\frac{(x-3)(x+2)}{|(x-5)| \cdot(x-1)}\)
Primero note el valor absoluto que rodea uno de los términos en el denominador. Los grados tanto del numerador como del denominador serán 2 lo que significa que la asíntota horizontal ocurrirá en un número. A medida que\(x\) se vuelve infinitamente grande, la función es aproximadamente:
\(f(x)=\frac{x^{2}}{x^{2}}\)
Entonces la asíntota horizontal es\(y=-1\) como\(x\) se vuelve infinitamente grande.
Por otro lado, a medida que\(x\) se vuelve infinitamente pequeña la función es aproximadamente:
\(f(x)=\frac{x^{2}}{-x^{2}}\)
Entonces la asíntota horizontal es\(y=-1\) como\(x\) se vuelve infinitamente pequeña.
En este caso, no se puede utilizar ciegamente la regla del coeficiente principal porque el valor absoluto cambia el signo.
Identificar las asíntotas horizontales si existen para las siguientes 3 funciones.
1. \(f(x)=\frac{3 x^{6}-72 x}{x^{6}+999}\)
Los grados del numerador y del denominatro son iguales por lo que es la asíntota horizontal\(y=3\).
2. \(h(x)=\frac{a x^{4}+b x^{3}+c x^{2}+d x+e}{f x^{4}+g x^{3}+h x^{2}}\)
Los grados del numerador y el denominador son iguales de nuevo por lo que la asíntota horizontal es\(y=\frac{a}{f}\)
3. \(g(x)=\frac{f(x)}{h(x)}\)
Como\(x\) se pone infinitamente grande,
\(g(x)=\frac{f(x)}{h(x)}=\frac{\frac{3 x^{6}-72 x}{x^{6}+999}}{\frac{a x^{4}+b x^{3}+c x^{2}+d x+e}{f x^{4}+g x^{3}+h x^{2}}} \approx \frac{3}{\frac{a}{f}}=\frac{3 f}{a}\)
Cuando estudies el cálculo, aprenderás las técnicas rigurosas que te permiten sentirte más seguro sobre resultados como este.
Revisar
Identificar las asíntotas horizontales, si existen, para las siguientes funciones.
1. \(f(x)=\frac{5 x^{4}-2 x}{x^{4}+32}\)
2. \(g(x)=\frac{3 x^{4}-2 x^{6}}{-x^{4}+2}\)
3. \(h(x)=\frac{3 x^{4}-5 x}{8 x^{3}+3 x^{4}}\)
4. \(j(x)=\frac{2 x^{3}-15 x}{-x^{4}+3}\)
5. \(k(x)=\frac{2 x^{5}-3 x}{5 x^{2}+3 x^{4}+2 x-7 x^{5}}\)
6. \(f(x)=\frac{a x^{14}+b x^{23}+c x^{12}+d x+e}{f x^{24}+g x^{23}+h x^{21}}\)
7. \(g(x)=\frac{(x-1)(x+4)}{|(x-2)| \cdot(x-1)}\)
8. Escribe una función que se ajuste a los siguientes criterios:
- Asíntotas verticales en\(x=1\) y\(x=4\)
- Ceros a 3 y 5
- Agujero cuando\(x=6\)
- Aíntota horizontal en\(y=\frac{2}{3}\)
9. Escribe una función que se ajuste a los siguientes criterios:
- Asíntotas verticales en\(x=-2\) y\(x=2\)
- Ceros en 1 y 5
- Agujero cuando\(x=3\)
- Asintota horizontal en\(y=1\)
10. Escribe una función que se ajuste a los siguientes criterios:
- Asíntotas verticales en\(x=0\) y\(x=3\)
- Ceros en 1 y 2
- Agujero cuando\(x=8\)
- Asintota horizontal en\(y=2\)
11. Escribe una función que se ajuste a los siguientes criterios:
- Aíntotas verticales a las 2 y 6
- Cero a 5
- Agujero cuando\(x=4\)
- Asintota horizontal en\(y=0\)
12. Escribe una función que se ajuste a los siguientes criterios:
- Aíntota vertical a las 4
- Ceros a 0 y 3
- Agujero en cuando\(x=5\)
- Sin asíntotas horizontales
Identificar las asíntotas verticales y horizontales de las siguientes funciones racionales.
13. \(f(x)=\frac{(x-5)(2 x+1)(x-3)}{(x-3)(4 x+5)(x-6)}\)
14. \(g(x)=\frac{x(x-1)(x+3)(x-5)}{3 x(x-1)(4 x+3)}\)
15. \(h(x)=\frac{(x-2)(x+3)(x-6)}{(x-4)(x+3)^{2}(x+2)}\)

