5.4: Desplazamiento vertical de funciones sinusoidales
- Page ID
- 107458
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Su conocimiento de las transformaciones, específicamente el desplazamiento vertical, se aplica directamente a las funciones sinusoidales. En la práctica, el boceto de las funciones de seno y coseno desplazado requiere una mayor atención al detalle y un etiquetado más cuidadoso que otras funciones. ¿Se puede describir con palabras la siguiente transformación?
\(f(x)=\sin x \rightarrow g(x)=-3 \sin x-4\)
¿En qué orden ocurren la reflexión, el estiramiento y el cambio? ¿Hay alguna diferencia?
Desplazamiento vertical de funciones sinusoidales
La forma general de una función sinusoidal es:
\(f(x)=\pm a \cdot \sin (b(x+c))+d\)
Recordemos que\(a\) controla la amplitud y los\(\pm\) controles de reflexión. Aquí podrás ver cómo\(d\) controla el desplazamiento vertical.
La forma más sencilla de pensar sobre el desplazamiento vertical de las funciones sinusoidales es enfocarse en el eje sinusoidal, la línea horizontal que atraviesa la mitad de la onda sinusoidal o coseno. Al inicio del problema identificar el desplazamiento vertical e inmediatamente dibujar el nuevo eje sinusoidal. Luego se procede a graficar la amplitud y reflexión alrededor de ese eje en contraposición al\(x\) eje.
A continuación se muestran las gráficas de las tres funciones siguientes:
\(f(x)=\sin x+3\)
\(g(x)=\sin x-2\)
\(h(x)=\sin x+\frac{1}{2}\)
Para dibujar estas gráficas, primero se dibuja el nuevo eje sinusoidal para cada gráfica. Después, se dibuja una onda sinusoidal completa para cada una. Anote los cinco puntos importantes que separan cada cuadrante para ayudar a tener una idea clara de la gráfica. No hay reflexiones en estas gráficas y todas tienen una amplitud de 1. Ahora mismo cada ciclo comienza en 0 y termina en\(2 \pi\) pero este no siempre será el caso.
Vea las porciones del siguiente video enfocadas en las traducciones verticales:
Ejemplos
Anteriormente, se le preguntó en qué orden se debe realizar el desplazamiento vertical y la reflexión y si importa. La siguiente transformación se puede describir de la siguiente manera.
\(f(x)=\sin x \rightarrow g(x)=-3 \sin x-4\)
Describa primero el estiramiento y la reflexión y luego el desplazamiento vertical. Esta es la forma más lógica de discutir la transformación verbalmente porque entonces los números como 3 y -4 pueden identificarse explícitamente en la gráfica.
El orden en la descripción de la transformación importa. Al describir las transformaciones verticales es más intuitivo describir simplemente las transformaciones en el mismo orden que el orden de las operaciones.
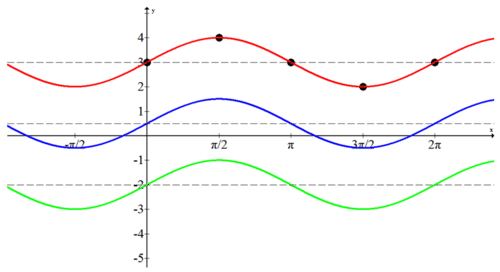
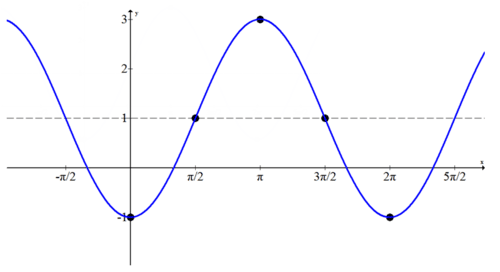
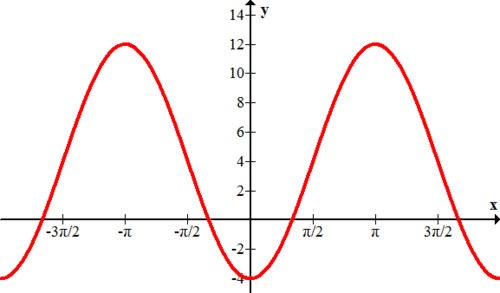
Identificar la ecuación de la siguiente gráfica de coseno transformado.
ya que no hay un eje sinusoidal dado, se debe determinar el desplazamiento vertical, estiramiento y reflexión. El pico ocurre en\((\pi, 3)\) y el canal ocurre en (0, -1) por lo que la línea horizontal directamente entre +3 y -1 es\(y=1\). ya que el eje sinusoidal ha sido desplazado hacia arriba en una unidad\(d=1\). A partir de esta altura, la gráfica va dos arriba y dos por debajo lo que significa que la amplitud es 2. ya que esta gráfica coseno inicia su ciclo en (0, -1) que es un punto más bajo, es un coseno negativo. La función es\(f(x)=-2 \cos x+1\)
Transforma la siguiente gráfica sinusoidal de dos maneras. Primero, transforma la gráfica sinusoidal desplazándola verticalmente hacia arriba 1 unidad y luego estirándola verticalmente por un factor de 2 unidades. Segundo, transforma la gráfica sinusoidal estirándola verticalmente por un factor de 2 unidades y luego desplazándola verticalmente hacia arriba 1 unidad.
Al hacer transformaciones ordenadas es bueno mostrar por dónde comienzas y dónde terminas para que puedas comparar y contrastar los resultados de manera efectiva. Vea cómo ambas transformaciones comienzan con una onda sinusoidal regular. Las dos columnas representan la secuencia de transformaciones que producen diferentes resultados.
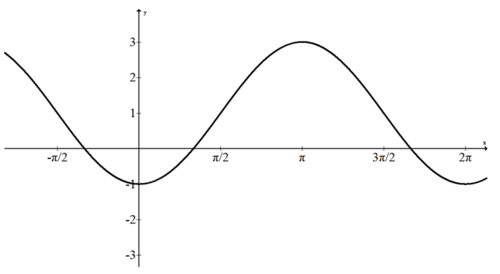
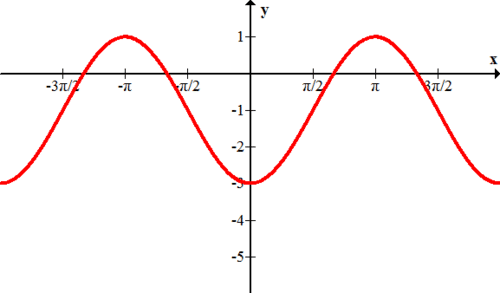
¿Qué ecuación modela la siguiente gráfica?
\(f(x)=3 \cdot \sin x-1\)
Grafique la siguiente función:\(f(x)=-2 \cdot \cos x+1\)
Primero dibuje el eje sinusoidal horizontal e identifique los cinco puntos principales para la onda coseno. Tenga cuidado de señalar que la amplitud es 2 y la onda coseno comienza y termina en un punto bajo debido al signo negativo.
Revisar
Grafique cada una de las siguientes funciones que hayan sufrido un estiramiento vertical, reflexión y/o un desplazamiento vertical.
1. \(f(x)=-2 \sin x+4\)
2. \(g(x)=\frac{1}{2} \cos x-1\)
3. \(h(x)=3 \sin x+2\)
4. \(j(x)=-1.5 \cos x+\frac{1}{2}\)
5. \(k(x)=\frac{2}{3} \sin x-3\)
Encuentra los valores mínimo y máximo de cada una de las siguientes funciones.
6. \(f(x)=-3 \sin x+1\)
7. \(g(x)=2 \cos x-4\)
8. \(h(x)=\frac{1}{2} \sin x+1\)
9. \(j(x)=-\cos x+5\)
10. \(k(x)=\sin (x)-1\)
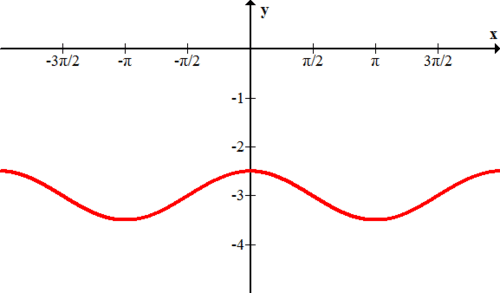
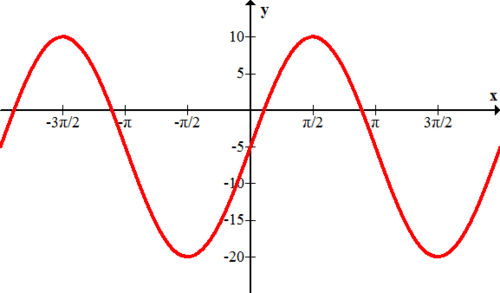
Dar la ecuación de cada función graficada a continuación.
11.
12.
13.
14.
15.