2.2.3: Triángulos rectos y rodamientos
- Page ID
- 107713
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\(\newcommand{\longvect}{\overrightarrow}\)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Direcciones basadas en puntos de brújula.
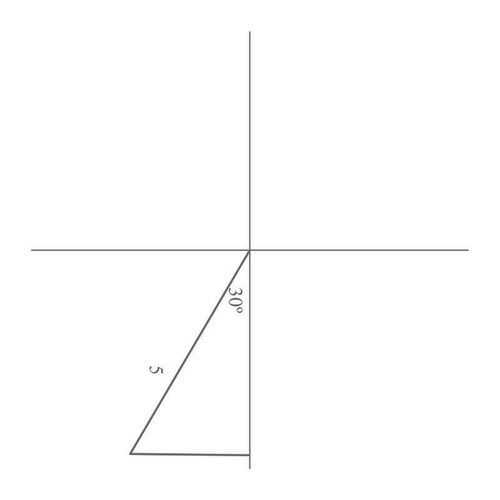
Mientras estás en un viaje de campamento con tus amigos, haces un viaje de orientación. Terminas en un curso que te lleva a caminar\(30^{\circ}\) al oeste de debido sur. Esto se representa como\(S30^{\circ}W\) (siempre comienza con N o S, luego el número de grados al este u oeste de ahí). Caminas hasta que estés a 5 millas de donde empezaste. ¿Es posible determinar qué tan lejos al oeste estás de donde iniciaste?
Cojinetes
Puedes usar triángulos rectos para encontrar distancias usando ángulos dados como rodamientos. En navegación, un rumbo es la dirección de un objeto a otro. En la navegación aérea, los rodamientos se dan como ángulos girados en sentido horario desde el norte.
La siguiente gráfica muestra un ángulo de 70 grados:
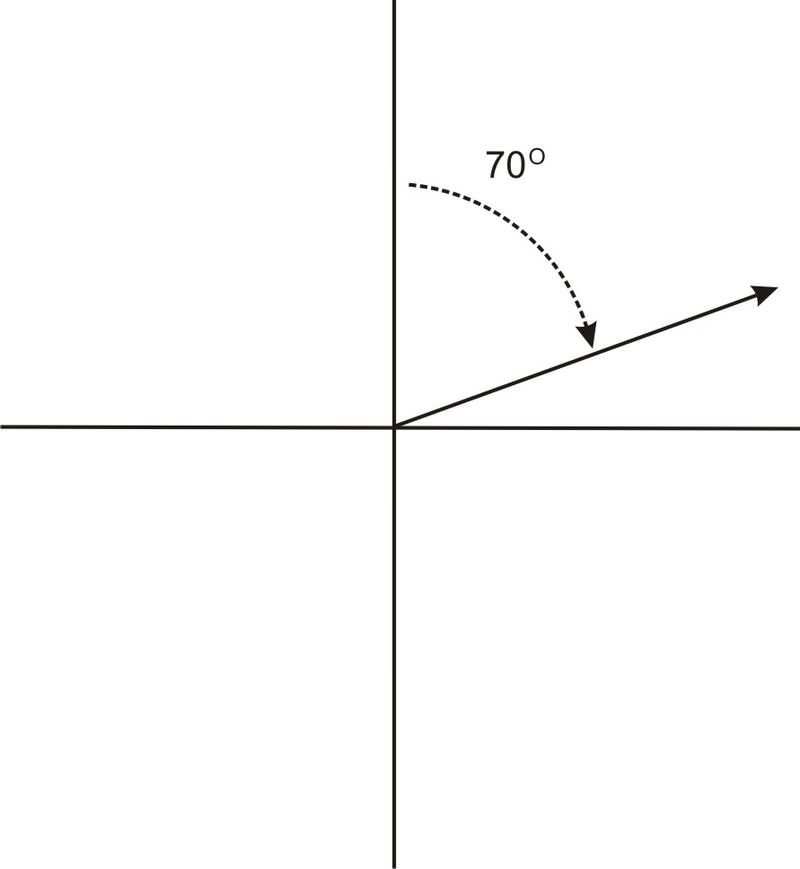
Es importante tener en cuenta que los ángulos en los problemas de navegación se miden de esta manera, y no de la misma manera en que los ángulos se miden de otra manera en trigonometría. Además, los ángulos en navegación y topografía también se pueden dar en términos de norte, este, sur y oeste. Por ejemplo,\(N70^{\circ}E\) se refiere a un ángulo de 70 grados al este de recto norte, mientras que\(N70^{\circ}W\) se refiere a un ángulo de 70 grados al oeste de recto norte. \(N70^{\circ}E\)es el mismo que el ángulo mostrado en la gráfica anterior. \(N70^{\circ}W\)resultaría en un ángulo en el segundo cuadrante, así:
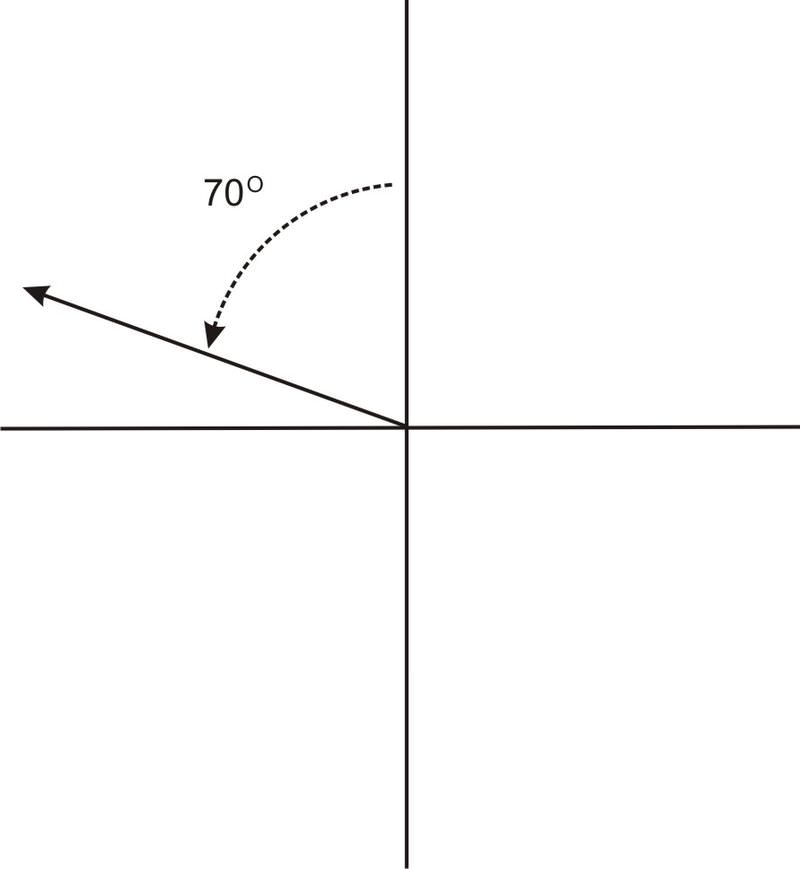
Ahora, veamos un problema donde encontramos la distancia usando triángulos rectos como rodamientos.
Un barco viaja en un\(N50^{\circ}E\) rumbo. El buque viaja hasta llegar al norte de un puerto que se encuentra a 10 millas náuticas al este del puerto del que se originó el buque. ¿Hasta dónde viajó el barco?
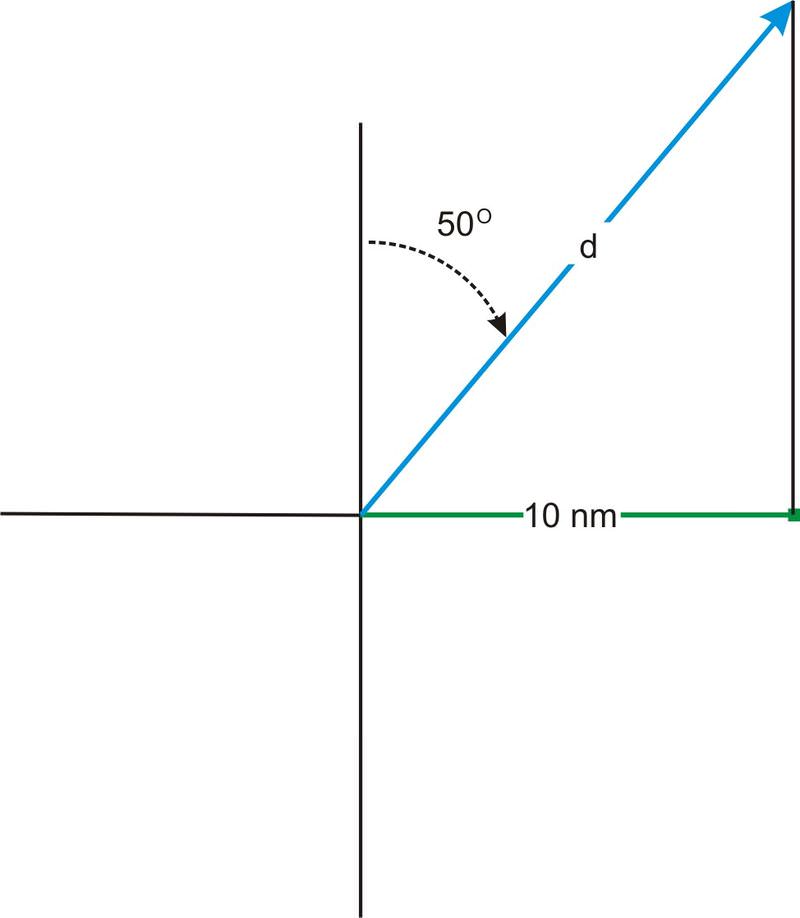
El ángulo entre d y 10 nm es el complemento de\(50^{\circ}\), que es\(40^{\circ}\). Por lo tanto podemos encontrar d usando la función coseno:
\(\begin{aligned} \cos 40^{\circ}&=\dfrac{\text{adjacent}}{\text{hypotenuse}}=\dfrac{10}{d} \\ \cos 40^{\circ}&=\dfrac{10}{d} \\ d \cos 40^{\circ}&=10 \\ d&=10 \cos 40^{\circ}\approx 13.05 \text{ nautical miles}\end{aligned}\)
Un avión vuela en un curso de\(S30^{\circ}E\), por 150 km. ¿Qué tan al sur está el avión de donde se originó?
Construye un triángulo usando la información conocida y luego usa la función coseno para resolver el problema:
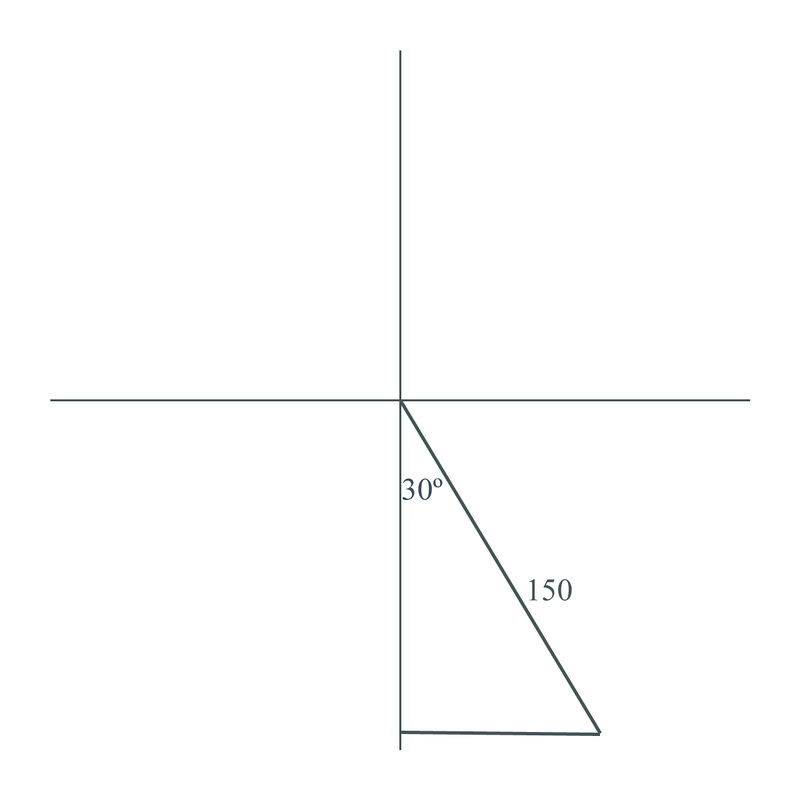
\(\begin{aligned} \cos 30^{\circ} &= \dfrac{\text{adjacent}}{\text{hypotenuse}}=\dfrac{y}{150} \\ \cos 30^{\circ} &=\dfrac{y}{150} \\ 150\cos 30^{\circ}&=y \\ y&=150 \cos 30^{\circ}\approx 130 \text{ km}\end{aligned}\)
Jean viaja a la escuela todos los días caminando 200 metros hacia el norte, y luego girando a la derecha y caminando 100 metros por eEast. Si hubiera caminado en línea recta, ¿cuál sería el ángulo entre su casa y la escuela si el inicio del ángulo se toma desde el norte? ¿Cuáles serían dos formas distintas de describir la dirección a tomar caminando ahí en línea recta, u\ sin g lo que hemos aprendido en esta sección?
A partir del triángulo dado anteriormente, podemos usar la función tangente para determinar el ángulo si ella hubiera caminado en línea recta.
\(\begin{aligned} \tan\theta &=\dfrac{\text{opposite}}{\text{adjacent}}= \dfrac{100}{200} \\ \tan\theta &=\dfrac{100}{200} \\ \theta &=26.57^{\circ} \end{aligned}\)
Una forma de describir su camino en línea recta es lo lejos al este del norte que está:\(N26.57^{\circ}E\)
Además, dado que sabemos que los rodamientos suelen estar basados fuera del norte, su movimiento puede describirse como simplemente un rodamiento de\(26.57^{\circ}\).
Anteriormente, se le dio alguna información sobre un viaje de senderismo, y le preguntaron “¿Es posible determinar qué tan al sur se encuentra de donde comenzó?”
Solución
La historia especificaba que caminaste por 5 millas desde tu punto de partida, en una dirección de\(S30^{\circ}W\). Aplicando estos datos con su comprensión de cómo construir un triángulo usando rodamientos, puede dibujar lo siguiente:
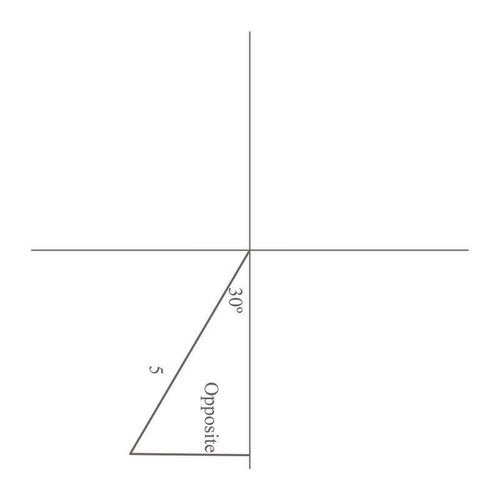
Esto demuestra que el lado opuesto del triángulo es lo que no se conoce. Por lo tanto, puede usar la función\ sin e para resolver el problema:
\(\begin{aligned} \sin 30^{\circ}&= \dfrac{\text{opposite}}{5} \\ \text{opposite }&= 5\sin 30^{\circ} \\ \text{opposite}&=(5)(.5)=2.5 \end{aligned}\)
Estás a 2.5 millas al oeste de donde empezaste.
Trazar un rumbo o rumbo de\(240^{\circ}\) en un sistema de coordenadas rectangulares.
Solución
Esto es lo mismo que\(S30^{\circ}W\) (recordemos que debido al sur es de 270 grados, por lo que 240 grados es 30 grados al oeste de ese) y se puede trazar como:
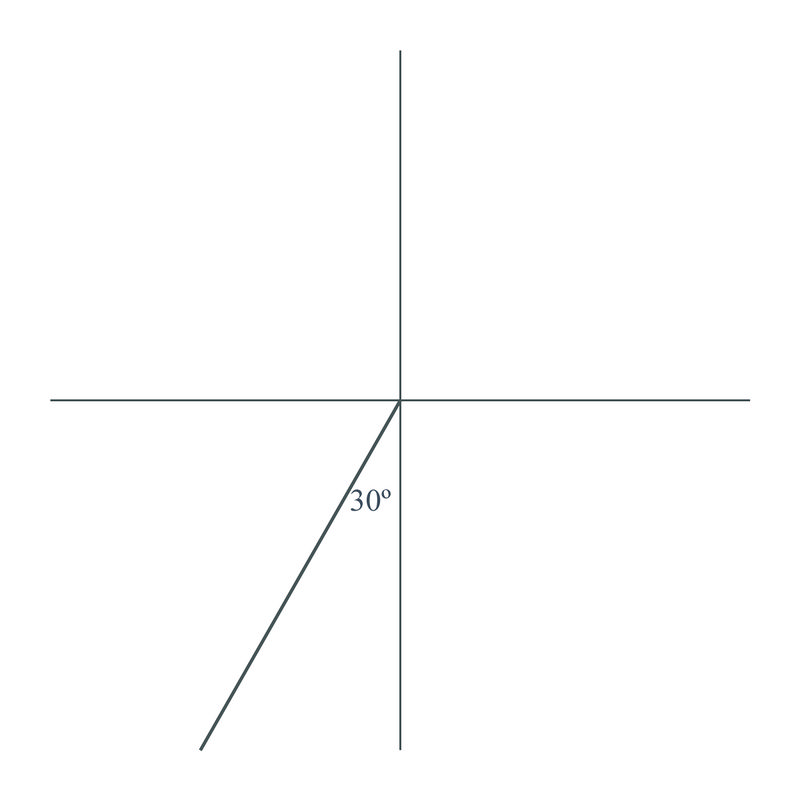
Scott está navegando en un curso de\(N15^{\circ}E\). ¿Qué rumbo tendría que tomar para regresar a donde vino?
Solución
En sentido contrario lo devolvería a su punto de partida. Esto sería\(S15^{\circ}W\).
Adam camina en un recorrido\(N 47^{\circ}E\) de 7 km. ¿Qué tan al oriente está Adán de donde partió?
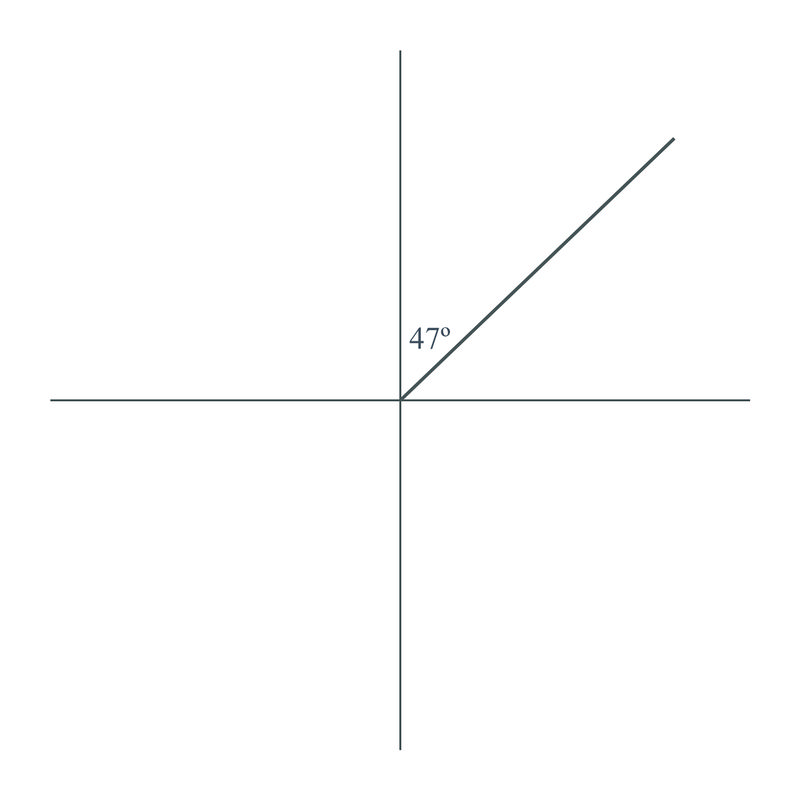
Solución
Encuentra la longitud del triángulo de arriba (que es lo lejos que viajó Adán hacia el este) por u\ sin g la función\ sin e:
\(\begin{aligned} \sin 47^{\circ}&=\dfrac{x}{7} \\ x&=7\sin 47^{\circ} \\ x&=(7)(.7313) \\ x&=5.1191 \end{aligned}\)
Se encuentra a 5.1191 km al este de donde inició.
Revisar
- Trazar un curso de\(N40^{\circ}E\) en un sistema de coordenadas rectangulares.
- Trazar un curso de\(60^{\circ}\) en un sistema de coordenadas rectangulares.
- Trazar un curso de\(S70^{\circ}W\) en un sistema de coordenadas rectangulares.
- Trazar un curso de\(S5^{\circ}W\) en un sistema de coordenadas rectangulares.
- Trazar un curso de\(N42^{\circ}W\) en un sistema de coordenadas rectangulares.
- Estás en un curso de\(N55^{\circ}E\). ¿Qué curso necesitarías tomar para regresar a donde vienes?
- Estás en un curso de\(S34^{\circ}W\). ¿Qué curso necesitarías tomar para regresar a donde vienes?
- Estás en un curso de\(N72^{\circ}W\). ¿Qué curso necesitarías tomar para regresar a donde vienes?
- Estás en un curso de\(S10^{\circ}E\). ¿Qué curso necesitarías tomar para regresar a donde vienes?
- Estás en un curso de\(N25^{\circ}W\). ¿Qué curso necesitarías tomar para regresar a donde vienes?
- Estás en un recorrido de\(47^{\circ}\) por 5 km. ¿Qué tan oriente estás de donde empezaste?
- Estás en un recorrido de\(S32^{\circ}E\) por 8 km. ¿Qué tan oriente estás de donde empezaste?
- Estás en un recorrido\(N15^{\circ}W\) de 10 km. ¿Qué tan lejos al oeste estás de donde empezaste?
- Estás en un recorrido\(S3^{\circ}W\) de 12 km. ¿Qué tan lejos al oeste estás de donde empezaste?
- Estás en un recorrido\(S67^{\circ}E\) de 6 km. ¿Qué tan oriente estás de donde empezaste?
Reseña (Respuestas)
Para ver las respuestas de Revisar, abra este archivo PDF y busque la sección 1.14.
El vocabulario
| Término | Definición |
|---|---|
| Cojinetes | El rumbo es cómo se mide la dirección en el mar. Norte es\(0^{\circ}\), este es\(90^{\circ}\), sur es\(180^{\circ}\), y poniente es\(270^{\circ}\). |
Recursos adicionales
Video: Modelos de Triángulo Recto - Ejemplo 1
Práctica: Triángulos rectos y rodamientos

