2.4.1: Funciones trigonométricas inversas
- Page ID
- 107696
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\(\newcommand{\longvect}{\overrightarrow}\)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Resolviendo para un ángulo dado una relación trigonométrica.
Funciones de trigonometría inversa y resolución de triángulos rectos
Un triángulo rectángulo tiene patas que miden 2 unidades y\(2 \sqrt{3}\) unidades. ¿Cuáles son las medidas de los ángulos agudos del triángulo?
Inversa de funciones trigonométricas
Hemos utilizado las funciones trigonométricas seno, coseno y tangente para encontrar la relación de lados particulares en un triángulo rectángulo dado un ángulo. En este concepto usaremos las inversas de estas funciones,\(\sin^{-1}\),\(\cos^{-1}\) y\(\tan^{-1}\), para encontrar la medida del ángulo cuando se conozca la relación de las longitudes laterales. Cuando escribimos\(\sin 30^{\circ}\) en nuestra calculadora, la calculadora va a una tabla y encuentra la relación trigonométrica asociada con\(30^{\circ}\), que es 12. Cuando usamos una función inversa le decimos a la calculadora que busque la relación y nos dé la medida del ángulo. Por ejemplo:\(\sin^{-1}\left(\dfrac{1}{2}\right)=30^{\circ}\). En tu calculadora presionarías\(2^{ND} SIN\) para obtener\(\sin^{-1}\) y luego escribir\(\dfrac{1}{2}\), cerrar el paréntesis y presionar ENTRAR. La pantalla de tu calculadora debe leerse\(\sin^{-1}\left(\dfrac{1}{2}\right)\) al presionar ENTRAR.
Encontremos la medida de ángulo\(A\) asociada con las siguientes proporciones y respuestas redondeadas al grado más cercano.
- \(\sin A=0.8336\)
- \(\tan A=1.3527\)
- \(\cos A=0.2785\)
Usando la calculadora obtenemos lo siguiente:
- \(\sin^{-1}(0.8336)\approx 56^{\circ}\)
- \(\tan^{-1} (1.3527)\approx 54^{\circ}\)
- \(\cos^{-1} (0.2785)\approx 74^{\circ}\)
Ahora, encontremos las medidas de los ángulos desconocidos en el triángulo mostrado y las respuestas redondeadas al grado más cercano.
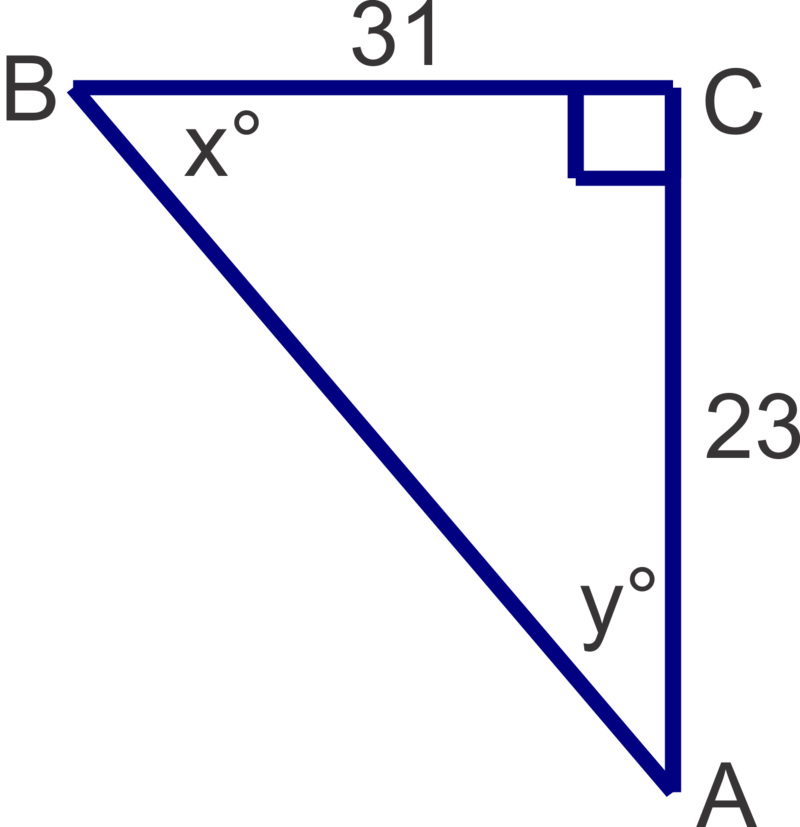
Podemos resolver por cualquiera\(x\) o por\(y\) primera vez. Si optamos por resolver por\(x\) primera vez, el 23 es opuesto y 31 es adyacente por lo que usaremos la relación tangente.
\(x=\tan^{-1} \left (\dfrac{23}{31}\right)\approx 37^{\circ}\).
Recordemos que en un triángulo rectángulo, los ángulos agudos son siempre complementarios, entonces\(90^{\circ} −37^{\circ} =53^{\circ}\), así\(y=53^{\circ}\). También podemos usar las longitudes de los lados y una relación trig para resolver para y:
\(y=\tan^{-1} \left(\dfrac{31}{23}\right)\approx 53^{\circ}\).
Por último, resolvamos el triángulo rectángulo que se muestra a continuación y redondeemos todas las respuestas a la décima más cercana.
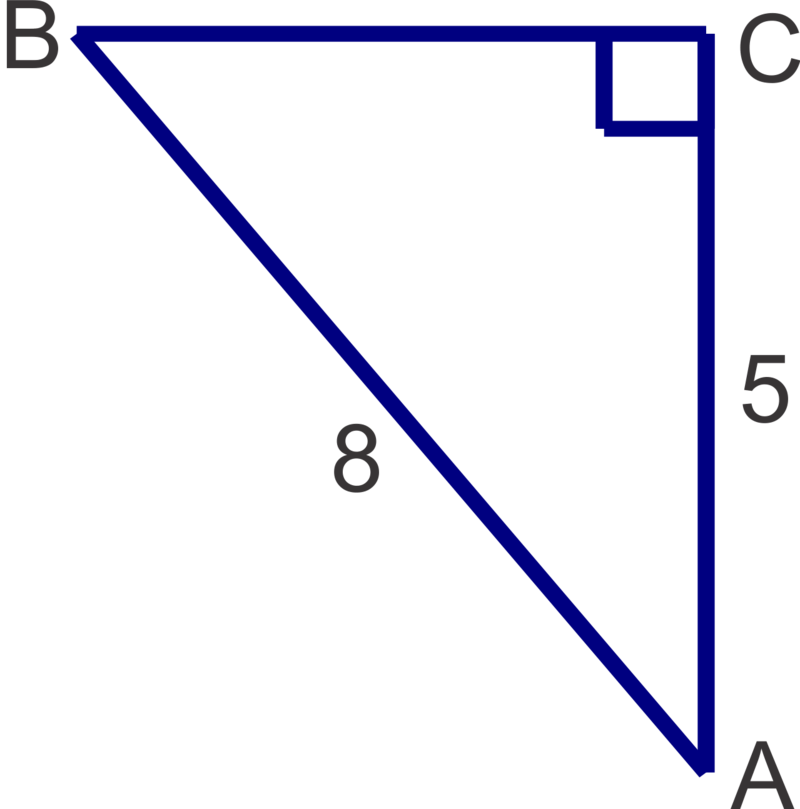
Podemos resolver\(B\) primero el ángulo\(A\) o el ángulo. Si elegimos resolver\(B\) primero para el ángulo, entonces 8 es la hipotenusa y 5 es la longitud del lado opuesto por lo que usaremos la relación sinusoidal.
\(\begin{aligned}\sin B&=\dfrac{5}{8} \\ m\angle B&=\sin^{-1} \left(\dfrac{5}{8}\right)\approx 38.7^{\circ}\end{aligned}\)
Ahora podemos encontrar A de dos maneras distintas.
Método 1: Podemos usar trigonometría y la relación coseno:
\(\begin{aligned}\cos A&=\dfrac{5}{8} \\ m\angle A&=\cos^{-1} \left(\dfrac{5}{8}\right)\approx 51.3^{\circ}\end{aligned}\)
Método 2: Podemos restar\(m\angle B\) de\(90^{\circ}\):\(90^{\circ} −38.7^{\circ} =51.3^{\circ}\) ya que los ángulos agudos en un triángulo rectángulo son siempre complementarios.
Cualquiera de los dos métodos es válido, pero ten cuidado con el Método 2 porque un error de cálculo del ángulo B haría que la medida que obtienes para el ángulo sea\(A\) incorrecta también.
Anteriormente, se le pidió que encontrara las medidas de los ángulos agudos del triángulo.
Solución
Primero, encontremos la hipotenusa, luego podemos resolver para cualquiera de los dos ángulos.
\(\begin{aligned} 2^2+(2\sqrt{3})^2 &=c^2 \\ 4+12&=c^2 \\ 16&=c^2 \\ c&=4\end{aligned}\)
Uno de los ángulos agudos tendrá un seno de\(\dfrac{2}{4}=\dfrac{1}{2}\).
\(\begin{aligned} \sin A&=\dfrac{1}{2}\\ m\angle A&=\sin^{-1} \dfrac{1}{2}=30^{\circ}\end{aligned}\)
Ahora podemos encontrar B restando\(m\angle A\) de\(90^{\circ}\):\(90^{\circ} −30^{\circ} =60^{\circ}\) ya que los ángulos agudos en un triángulo rectángulo son siempre complementarios.
Encuentra la medida del ángulo\(A\).
Solución
\(\begin{aligned} \sin A&=0.2894 \\ \sin^{-1}(0.2894) &\approx 17^{\circ} \end{aligned}\)
Encuentra la medida del ángulo\(A\).
Solución
\(\begin{aligned} \tan A&=2.1432 \\ \tan^{-1} (2.1432)&\approx 65^{\circ} \end{aligned}\)
Encuentra la medida del ángulo\(A\).
Solución
\(\begin{aligned} \cos A&=0.8911 \\ \cos^{-1} (0.8911) &\approx 27^{\circ}\end{aligned}\)
Encuentra las medidas de los ángulos desconocidos en el triángulo mostrado. Respuestas redondas al grado más cercano.
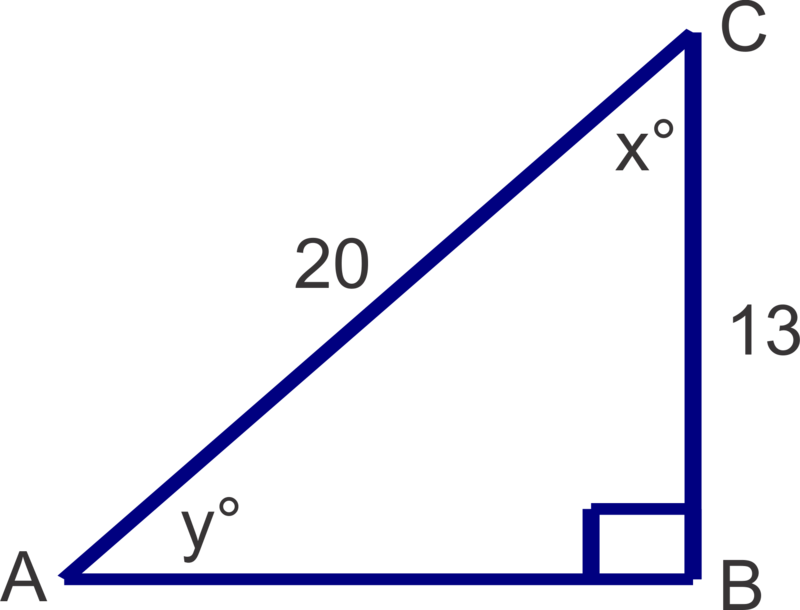
Solución
\(x=\cos^{-1} \left(\dfrac{13}{20}\right)\approx 49^{\circ} ; \quad y=\sin^{-1}(\dfrac{13}{20})\approx 41^{\circ}\)
Resuelve el triángulo. Redondear longitudes laterales a la décima más cercana y ángulos al grado más cercano.
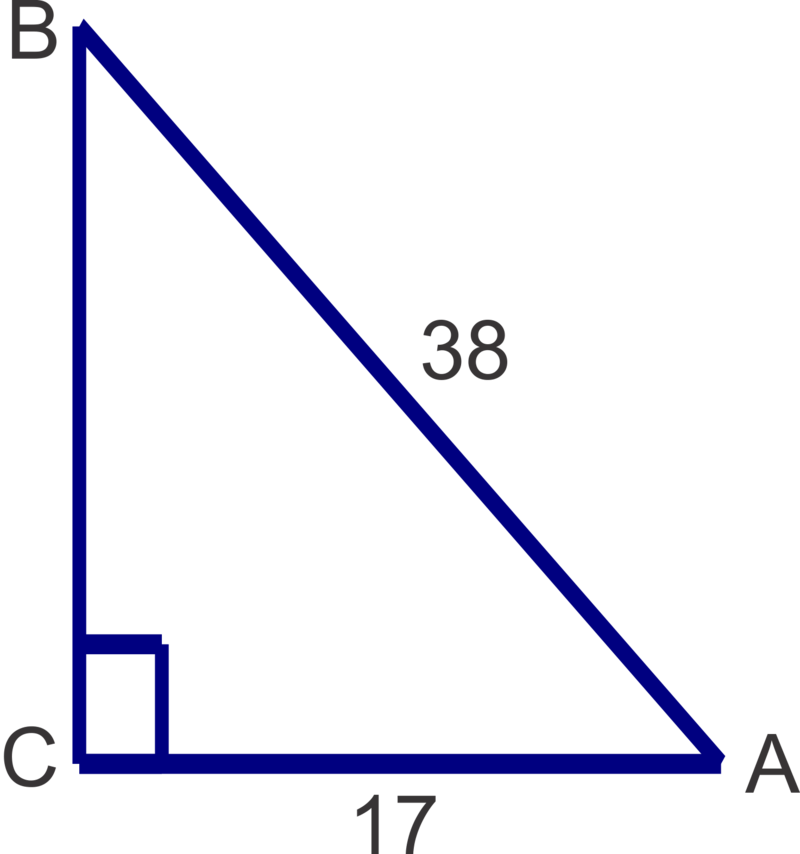
Solución
\(m\angle A=\cos^{-1} (\dfrac{17}{38})\approx 63^{\circ} ; m\angle B=\sin^{-1}(\dfrac{17}{38})\approx 27^{\circ} ; a=\sqrt{38^2−17^2} \approx 34.0\)
Revisar
Usa tu calculadora para encontrar la medida de\(\angle B\). Respuestas redondas al grado más cercano.
- \(\tan B=0.9523\)
- \(\sin B=0.8659\)
- \(\cos B=0.1568\)
- \(\sin B=0.2234\)
- \(\cos B=0.4855\)
- \(\tan B=0.3649\)
Encuentra las medidas de los ángulos agudos desconocidos. Medidas redondas al grado más cercano.
-
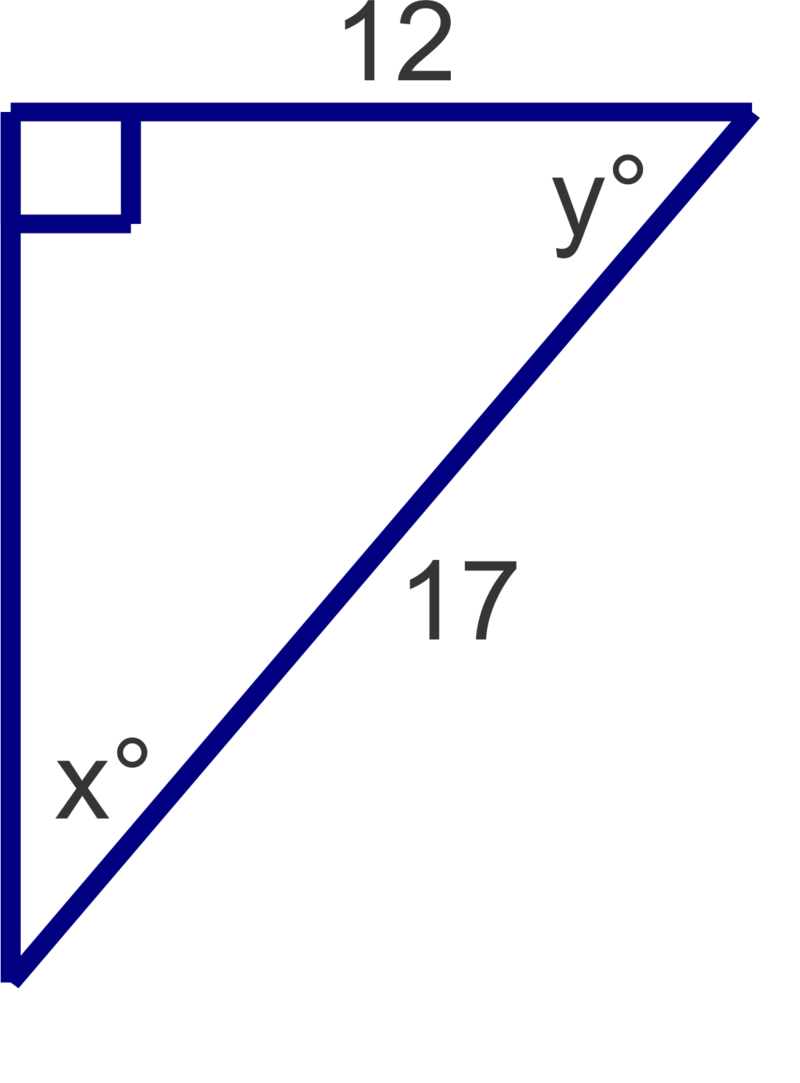
Figura\(\PageIndex{5}\) -
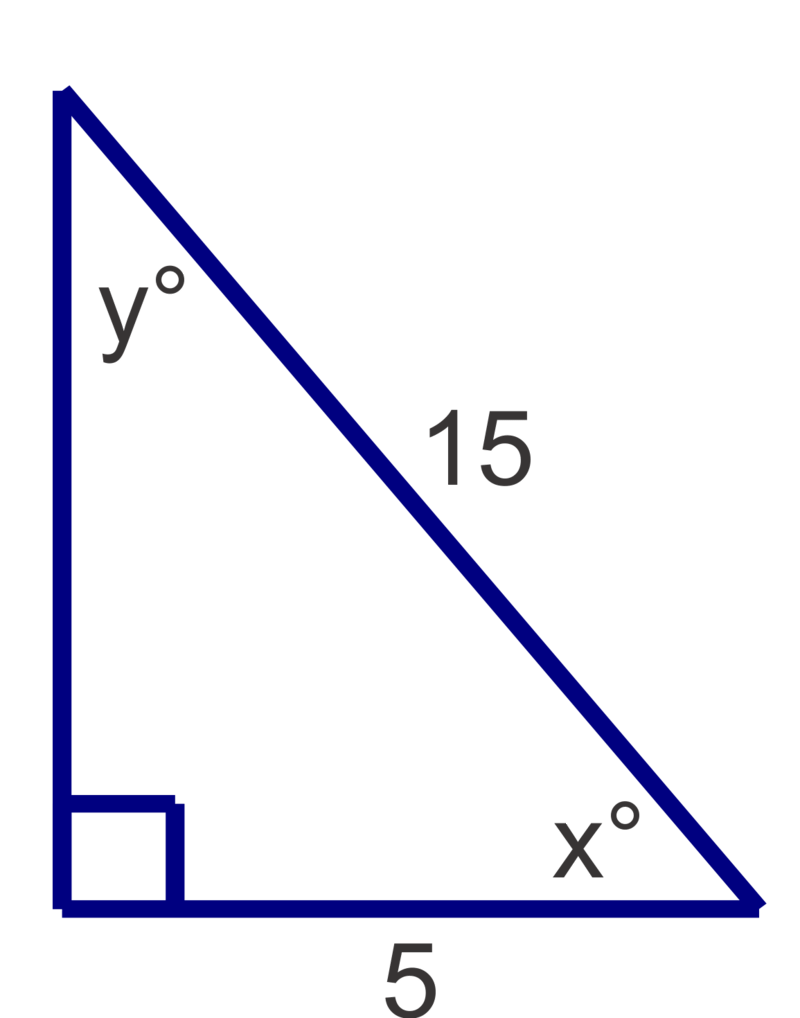
Figura\(\PageIndex{6}\) -
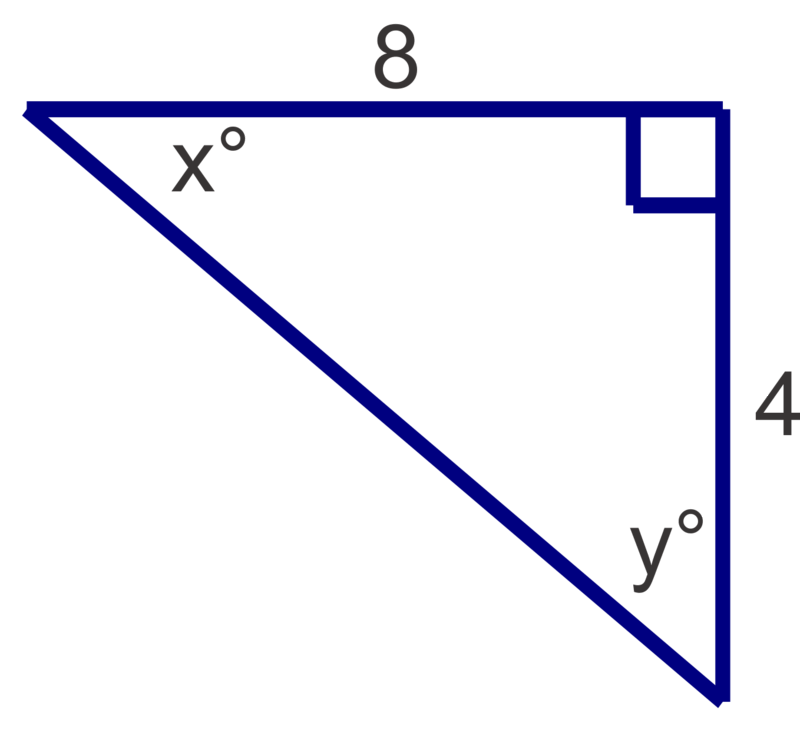
Figura\(\PageIndex{7}\) -
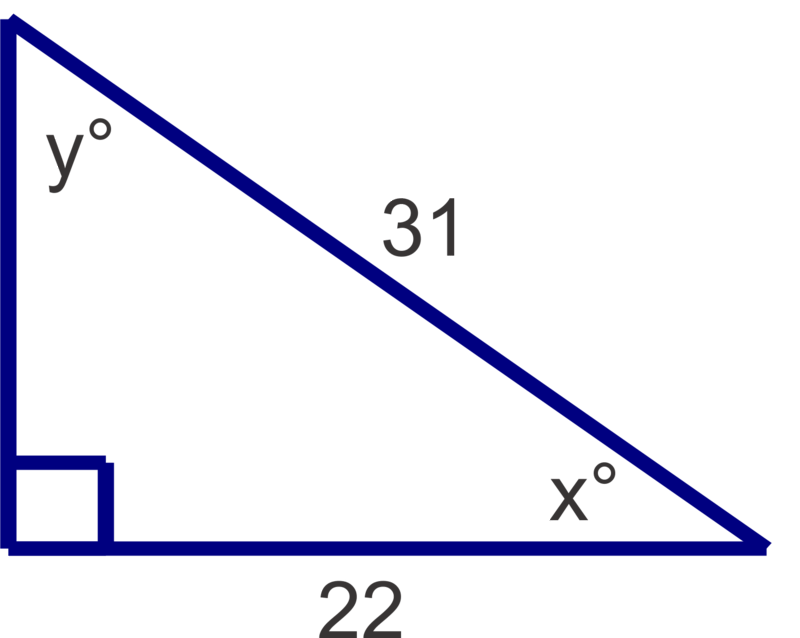
Figura\(\PageIndex{8}\) -
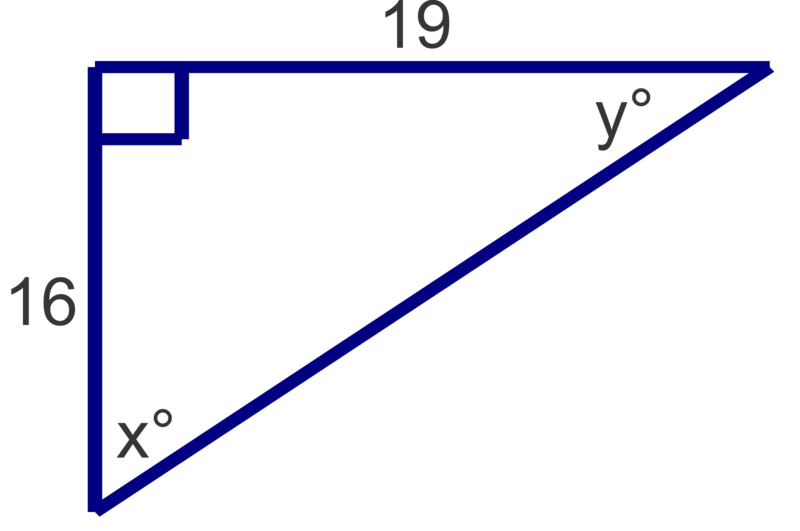
Figura\(\PageIndex{9}\) -
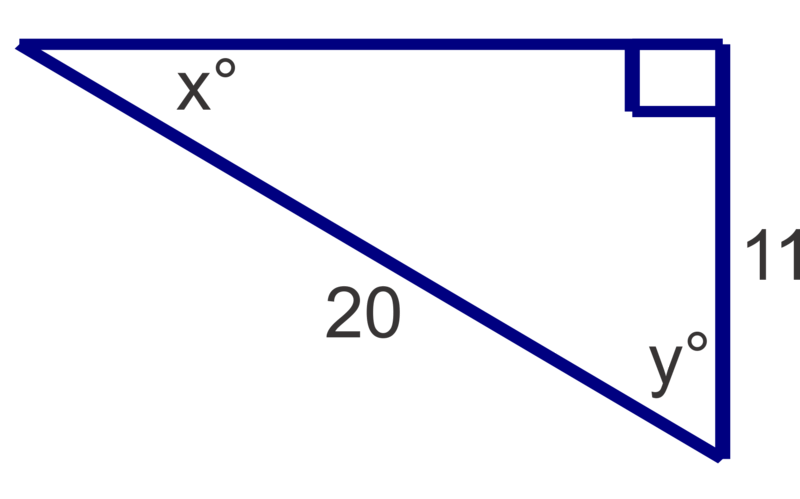
Figura\(\PageIndex{10}\)
Resuelve los siguientes triángulos rectos. El ángulo redondo mide al grado más cercano y las longitudes laterales al décimo más cercano.
-
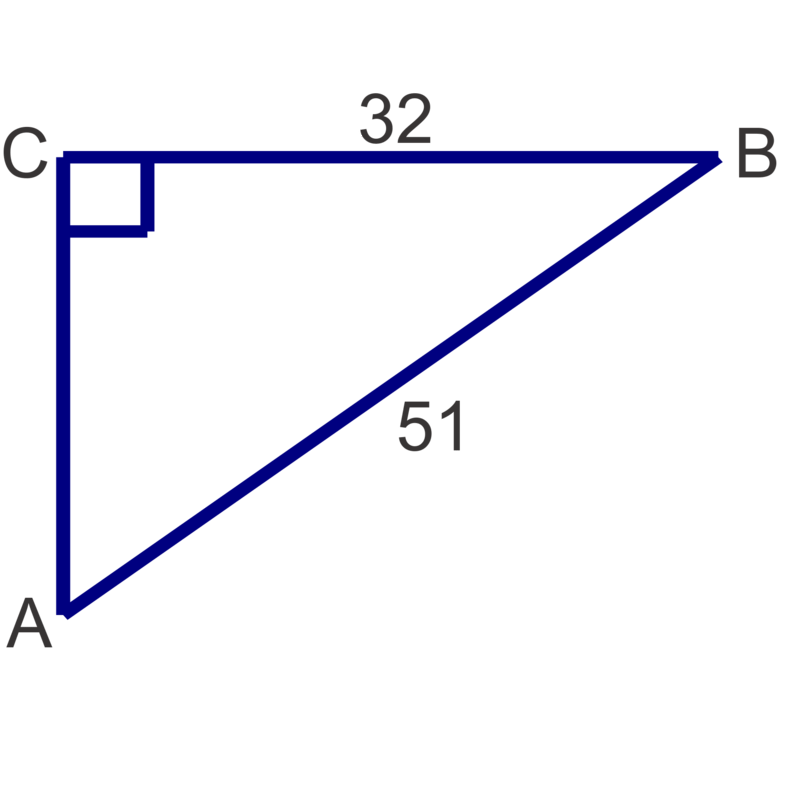
Figura\(\PageIndex{11}\) -
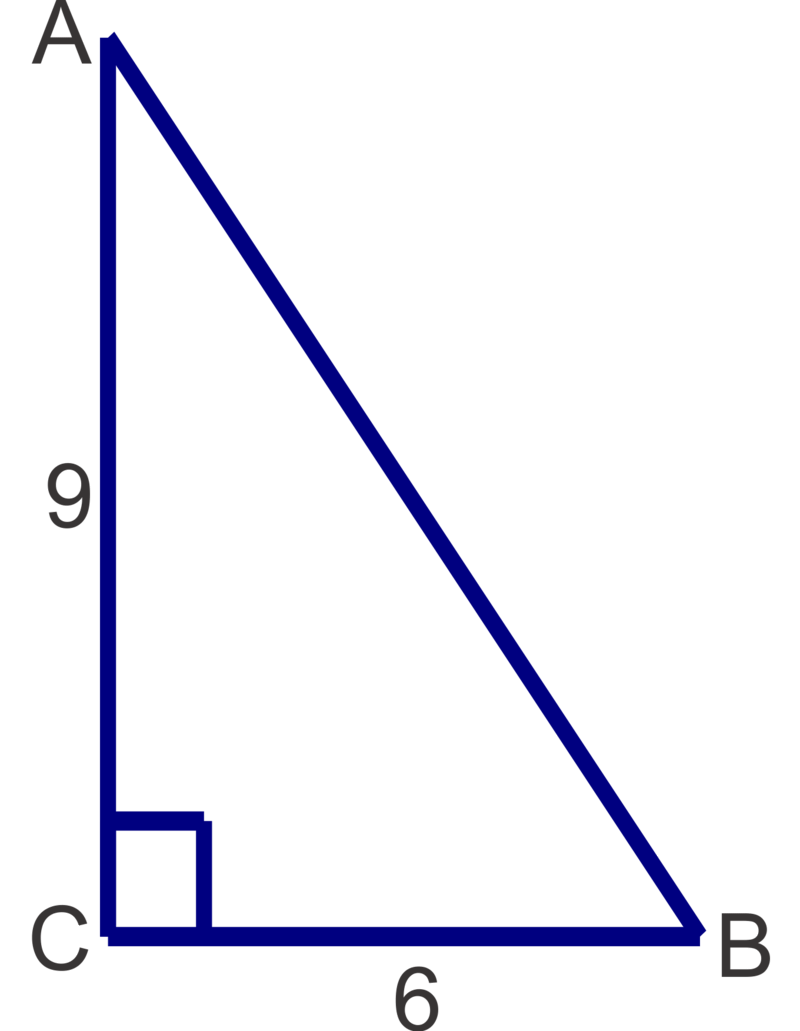
Figura\(\PageIndex{12}\) -
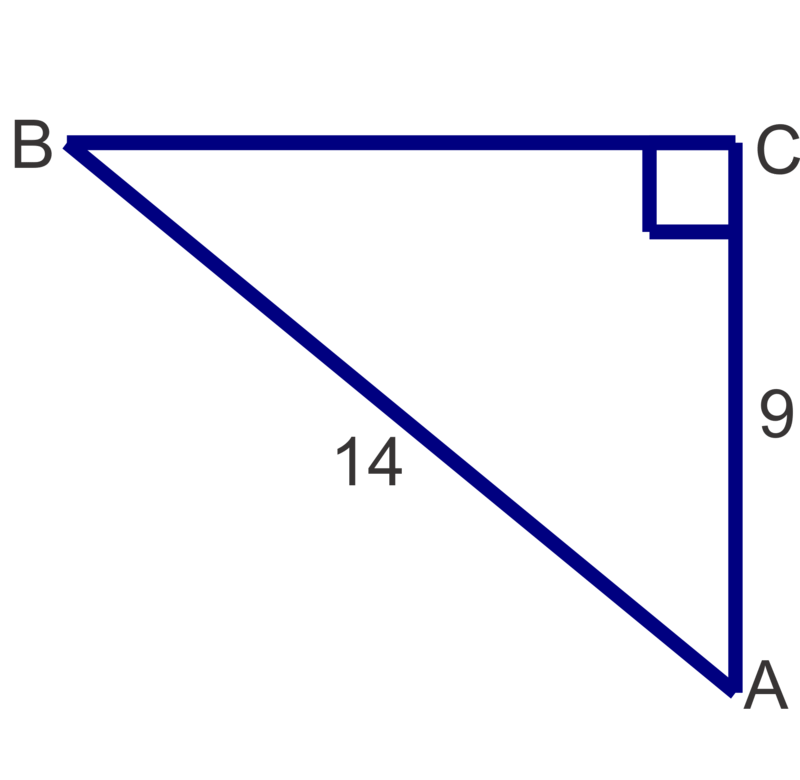
Figura\(\PageIndex{13}\)
Respuestas para problemas de revisión
Para ver las respuestas de Revisar, abra este archivo PDF y busque la sección 13.3.
Recursos adicionales
Video: Evaluación de funciones trigonométricas inversas sin usar la calculadora - Descripción general
Práctica: Funciones trigonométricas inversas

